- 2023-06-25 发布 |
- 37.5 KB |
- 24页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018年安徽省中考数学试卷
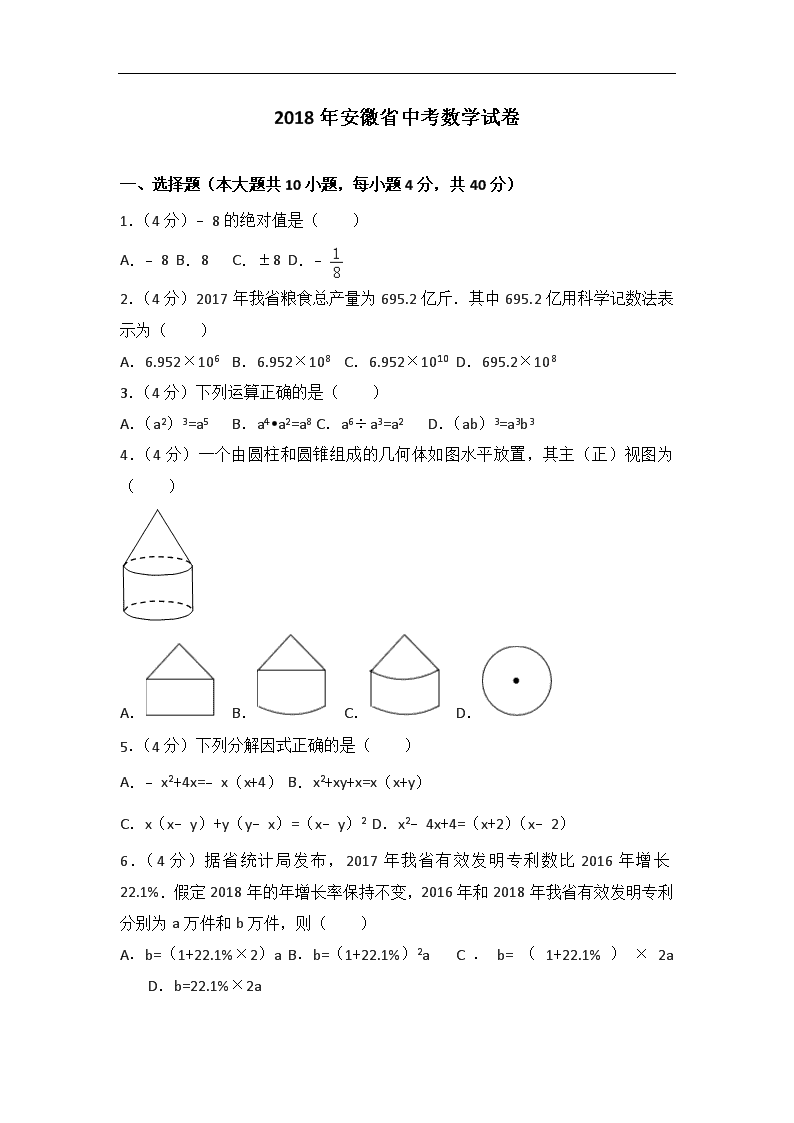
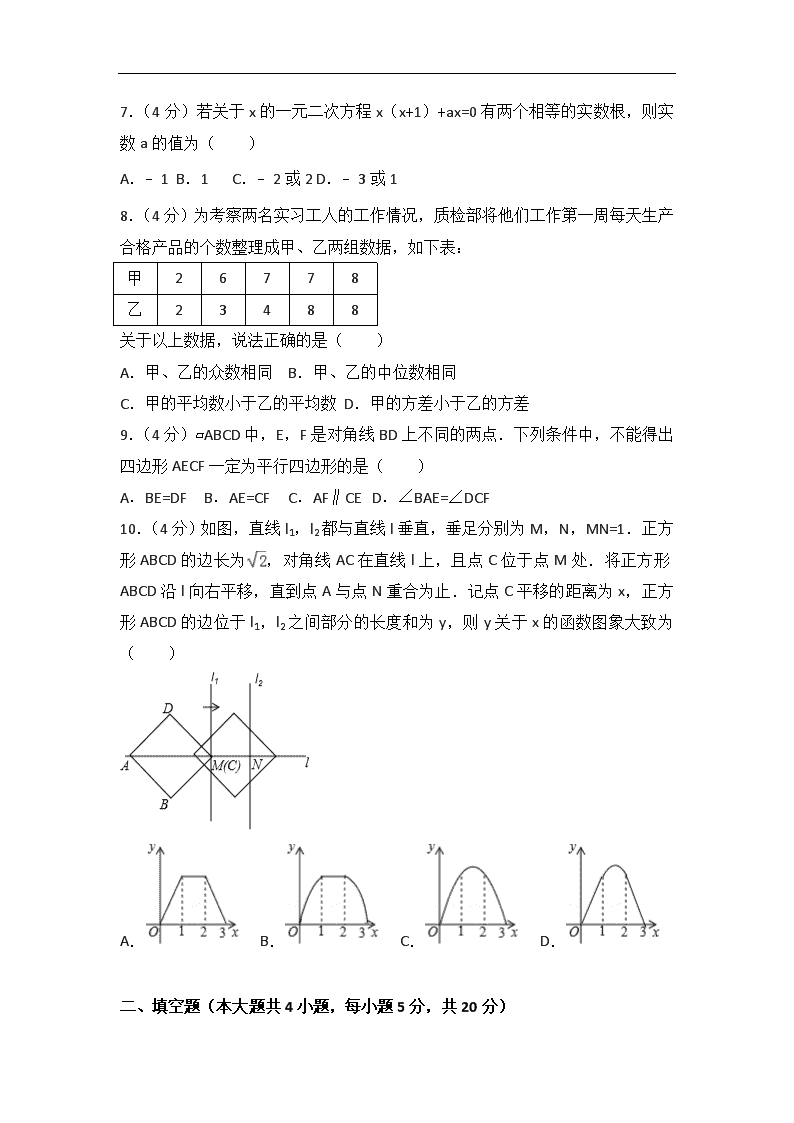
2018年安徽省中考数学试卷 一、选择题(本大题共10小题,每小题4分,共40分) 1.(4分)﹣8的绝对值是( ) A.﹣8 B.8 C.±8 D.﹣ 2.(4分)2017年我省粮食总产量为695.2亿斤.其中695.2亿用科学记数法表示为( ) A.6.952×106 B.6.952×108 C.6.952×1010 D.695.2×108 3.(4分)下列运算正确的是( ) A.(a2)3=a5 B.a4•a2=a8 C.a6÷a3=a2 D.(ab)3=a3b3 4.(4分)一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为( ) A. B. C. D. 5.(4分)下列分解因式正确的是( ) A.﹣x2+4x=﹣x(x+4) B.x2+xy+x=x(x+y) C.x(x﹣y)+y(y﹣x)=(x﹣y)2 D.x2﹣4x+4=(x+2)(x﹣2) 6.(4分)据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则( ) A.b=(1+22.1%×2)a B.b=(1+22.1%)2a C.b=(1+22.1%)×2a D.b=22.1%×2a 7.(4分)若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( ) A.﹣1 B.1 C.﹣2或2 D.﹣3或1 8.(4分)为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据,如下表: 甲 2 6 7 7 8 乙 2 3 4 8 8 关于以上数据,说法正确的是( ) A.甲、乙的众数相同 B.甲、乙的中位数相同 C.甲的平均数小于乙的平均数 D.甲的方差小于乙的方差 9.(4分)▱ABCD中,E,F是对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( ) A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF 10.(4分)如图,直线l1,l2都与直线l垂直,垂足分别为M,N,MN=1.正方形ABCD的边长为,对角线AC在直线l上,且点C位于点M处.将正方形ABCD沿l向右平移,直到点A与点N重合为止.记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y关于x的函数图象大致为( ) A. B. C. D. 二、填空题(本大题共4小题,每小题5分,共20分) 11.(5分)不等式>1的解集是 . 12.(5分)如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= °. 13.(5分)如图,正比例函数y=kx与反比例函数y=的图象有一个交点A(2,m),AB⊥x轴于点B.平移直线y=kx,使其经过点B,得到直线l,则直线l对应的函数表达式是 . 14.(5分)矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为 . 三、解答题(本大题共2小题,每小题8分,满分16分) 15.(8分)计算:50﹣(﹣2)+×. 16.(8分)《孙子算经》中有这样一道题,原文如下: 今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何? 大意为: 今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家? 请解答上述问题. 四、解答题(本大题共2小题,每小题8分,满分16分) 17.(8分)如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点. (1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),画出线段A1B1; (2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1,画出线段A2B1; (3)以A,A1,B1,A2为顶点的四边形AA1B1A2的面积是 个平方单位. 18.(8分)观察以下等式: 第1个等式:++×=1, 第2个等式:++×=1, 第3个等式:++×=1, 第4个等式:++×=1, 第5个等式:++×=1, …… 按照以上规律,解决下列问题: (1)写出第6个等式: ; (2)写出你猜想的第n个等式: (用含n的等式表示),并证明. 五、解答题(本大题共2小题,每小题10分,满分20分) 19.(10分)为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB= ∠FED),在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米?(结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02) 20.(10分)如图,⊙O为锐角△ABC的外接圆,半径为5. (1)用尺规作图作出∠BAC的平分线,并标出它与劣弧的交点E(保留作图痕迹,不写作法); (2)若(1)中的点E到弦BC的距离为3,求弦CE的长. 六、解答题(本大题满分12分) 21.(12分)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下: (1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ; (2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由; (3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率. 七、解答题(本题满分12分) 22.(12分)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现: ①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元; ②花卉的平均每盆利润始终不变. 小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元). (1)用含x的代数式分别表示W1,W2; (2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少? 八、解答题(本题满分14分) 23.(14分)如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E.点M为BD中点,CM的延长线交AB于点F. (1)求证:CM=EM; (2)若∠BAC=50°,求∠EMF的大小; (3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM. 2018年安徽省中考数学试卷 参考答案与试题解析 一、选择题(本大题共10小题,每小题4分,共40分) 1.(4分)﹣8的绝对值是( ) A.﹣8 B.8 C.±8 D.﹣ 【分析】计算绝对值要根据绝对值的定义求解.第一步列出绝对值的表达式;第二步根据绝对值定义去掉这个绝对值的符号. 【解答】解:∵﹣8<0,∴|﹣8|=8. 故选:B. 2.(4分)2017年我省粮食总产量为695.2亿斤.其中695.2亿用科学记数法表示为( ) A.6.952×106 B.6.952×108 C.6.952×1010 D.695.2×108 【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数. 【解答】解:695.2亿=695 2000 0000=6.952×1010, 故选:C. 3.(4分)下列运算正确的是( ) A.(a2)3=a5 B.a4•a2=a8 C.a6÷a3=a2 D.(ab)3=a3b3 【分析】根据同底数幂的除法法则,同底数幂的乘法的运算方法,以及幂的乘方与积的乘方的运算方法,逐项判定即可. 【解答】解:∵(a2)3=a6, ∴选项A不符合题意; ∵a4•a2=a6, ∴选项B不符合题意; ∵a6÷a3=a3, ∴选项C不符合题意; ∵(ab)3=a3b3, ∴选项D符合题意. 故选:D. 4.(4分)一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为( ) A. B. C. D. 【分析】根据从正面看得到的图形是主视图,可得答案. 【解答】解:从正面看上边是一个三角形,下边是一个矩形, 故选:A. 5.(4分)下列分解因式正确的是( ) A.﹣x2+4x=﹣x(x+4) B.x2+xy+x=x(x+y) C.x(x﹣y)+y(y﹣x)=(x﹣y)2 D.x2﹣4x+4=(x+2)(x﹣2) 【分析】直接利用公式法以及提取公因式法分解因式分别分析得出答案. 【解答】解:A、﹣x2+4x=﹣x(x﹣4),故此选项错误; B、x2+xy+x=x(x+y+1),故此选项错误; C、x(x﹣y)+y(y﹣x)=(x﹣y)2,故此选项正确; D、x2﹣4x+4=(x﹣2)2,故此选项错误; 故选:C. 6.(4分)据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则( ) A.b=(1+22.1%×2)a B.b=(1+22.1%)2a C.b=(1+22.1%)×2a D.b=22.1%×2a 【分析】根据2016年的有效发明专利数×(1+年平均增长率)2=2018年的有效发明专利数. 【解答】解:因为2016年和2018年我省有效发明专利分别为a万件和b万件,所以b=(1+22.1%)2a. 故选:B. 7.(4分)若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( ) A.﹣1 B.1 C.﹣2或2 D.﹣3或1 【分析】将原方程变形为一般式,根据根的判别式△=0即可得出关于a的一元二次方程,解之即可得出结论. 【解答】解:原方程可变形为x2+(a+1)x=0. ∵该方程有两个相等的实数根, ∴△=(a+1)2﹣4×1×0=0, 解得:a=﹣1. 故选:A. 8.(4分)为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据,如下表: 甲 2 6 7 7 8 乙 2 3 4 8 8 关于以上数据,说法正确的是( ) A.甲、乙的众数相同 B.甲、乙的中位数相同 C.甲的平均数小于乙的平均数 D.甲的方差小于乙的方差 【分析】根据一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数;对于n个数x1,x2,…,xn,则x¯=(x1+x2+…+xn)就叫做这n个数的算术平均数;s2=[(x1﹣x¯)2+(x2﹣x¯)2+…+(xn﹣x¯)2]进行计算即可. 【解答】解:A、甲的众数为7,乙的众数为8,故原题说法错误; B、甲的中位数为7,乙的中位数为4,故原题说法错误; C、甲的平均数为6,乙的平均数为5,故原题说法错误; D、甲的方差为4.4,乙的方差为6.4,甲的方差小于乙的方差,故原题说法正确; 故选:D. 9.(4分)▱ABCD中,E,F是对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( ) A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF 【分析】连接AC与BD相交于O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF即可,然后根据各选项的条件分析判断即可得解. 【解答】解:如图,连接AC与BD相交于O, 在▱ABCD中,OA=OC,OB=OD, 要使四边形AECF为平行四边形,只需证明得到OE=OF即可; A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意; B、若AE=CF,则无法判断OE=OE,故本选项符合题意; C、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意; D、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项不符合题意; 故选:B. 10.(4分)如图,直线l1,l2都与直线l垂直,垂足分别为M,N,MN=1.正方形ABCD的边长为,对角线AC在直线l上,且点C位于点M处.将正方形ABCD沿l向右平移,直到点A与点N重合为止.记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y关于x的函数图象大致为( ) A. B. C. D. 【分析】当0<x≤1时,y=2x,当1<x≤2时,y=2,当2<x≤3时,y=﹣2x+6,由此即可判断; 【解答】解:当0<x≤1时,y=2x, 当1<x≤2时,y=2, 当2<x≤3时,y=﹣2x+6, ∴函数图象是A, 故选:A. 二、填空题(本大题共4小题,每小题5分,共20分) 11.(5分)不等式>1的解集是 x>10 . 【分析】根据解一元一次不等式得基本步骤依次计算可得. 【解答】解:去分母,得:x﹣8>2, 移项,得:x>2+8, 合并同类项,得:x>10, 故答案为:x>10. 12.(5分)如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= 60 °. 【分析】连接OA,根据菱形的性质得到△AOB是等边三角形,根据切线的性质求出∠AOD,同理计算即可. 【解答】解:连接OA, ∵四边形ABOC是菱形, ∴BA=BO, ∵AB与⊙O相切于点D, ∴OD⊥AB, ∵点D是AB的中点, ∴直线OD是线段AB的垂直平分线, ∴OA=OB, ∴△AOB是等边三角形, ∵AB与⊙O相切于点D, ∴OD⊥AB, ∴∠AOD=∠AOB=30°, 同理,∠AOE=30°, ∴∠DOE=∠AOD+∠AOE=60°, 故答案为:60. 13.(5分)如图,正比例函数y=kx与反比例函数y=的图象有一个交点A(2,m),AB⊥x轴于点B.平移直线y=kx,使其经过点B,得到直线l,则直线l对应的函数表达式是 y=x﹣3 . 【分析】首先利用图象上点的坐标特征得出A点坐标,进而得出正比例函数解析式,再利用平移的性质得出答案. 【解答】解:∵正比例函数y=kx与反比例函数y=的图象有一个交点A(2,m), ∴2m=6, 解得:m=3, 故A(2,3), 则3=2k, 解得:k=, 故正比例函数解析式为:y=x, ∵AB⊥x轴于点B,平移直线y=kx,使其经过点B, ∴B(2,0), ∴设平移后的解析式为:y=x+b, 则0=3+b, 解得:b=﹣3, 故直线l对应的函数表达式是:y=x﹣3. 故答案为:y=x﹣3. 14.(5分)矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为 或3 . 【分析】根据勾股定理求出BD,分PD=DA、P′D=P′A两种情况,根据相似三角形的性质计算. 【解答】解:∵四边形ABCD为矩形, ∴∠BAD=90°, ∴BD==10, 当PD=DA=8时,BP=BD﹣PD=2, ∵△PBE∽△DBC, ∴=,即=, 解得,PE=, 当P′D=P′A时,点P′为BD的中点, ∴P′E′=CD=3, 故答案为:或3. 三、解答题(本大题共2小题,每小题8分,满分16分) 15.(8分)计算:50﹣(﹣2)+×. 【分析】首先计算零次幂和乘法,然后再计算加减即可. 【解答】解:原式=1+2+4=7. 16.(8分)《孙子算经》中有这样一道题,原文如下: 今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何? 大意为: 今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家? 请解答上述问题. 【分析】设城中有x户人家,根据鹿的总数是100列出方程并解答. 【解答】解:设城中有x户人家, 依题意得:x+=100 解得x=75. 答:城中有75户人家. 四、解答题(本大题共2小题,每小题8分,满分16分) 17.(8分)如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点. (1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),画出线段A1B1; (2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1,画出线段A2B1; (3)以A,A1,B1,A2为顶点的四边形AA1B1A2的面积是 20 个平方单位. 【分析】(1)以点O为位似中心,将线段AB放大为原来的2倍,即可画出线段A1B1; (2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1,即可画出线段A2B1; (3)连接AA2,即可得到四边形AA1B1A2为正方形,进而得出其面积. 【解答】解:(1)如图所示,线段A1B1即为所求; (2)如图所示,线段A2B1即为所求; (3)由图可得,四边形AA1B1A2为正方形, ∴四边形AA1B1A2的面积是()2=()2=20. 故答案为:20. 18.(8分)观察以下等式: 第1个等式:++×=1, 第2个等式:++×=1, 第3个等式:++×=1, 第4个等式:++×=1, 第5个等式:++×=1, …… 按照以上规律,解决下列问题: (1)写出第6个等式: ; (2)写出你猜想的第n个等式: (用含n的等式表示),并证明. 【分析】以序号n为前提,依此观察每个分数,可以用发现,每个分母在n的基础上依次加1,每个分子分别是1和n﹣1 【解答】解:(1)根据已知规律,第6个分式分母为6和7,分子分别为1和5 故应填: (2)根据题意,第n个分式分母为n和n+1,分子分别为1和n﹣1 故应填: 证明:= ∴等式成立 五、解答题(本大题共2小题,每小题10分,满分20分) 19.(10分)为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米?(结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02) 【分析】根据平行线的性质得出∠FED=45°.解等腰直角△DEF,得出DE=DF=1.8米,EF=DE=米.证明∠AEF=90°.解直角△AEF,求出AE=EF•tan∠AFE≈18.036米.再解直角△ABE,即可求出AB=AE•sin∠AEB≈18米. 【解答】解:由题意,可得∠FED=45°. 在直角△DEF中,∵∠FDE=90°,∠FED=45°, ∴DE=DF=1.8米,EF=DE=米. ∵∠AEB=∠FED=45°, ∴∠AEF=180°﹣∠AEB﹣∠FED=90°. 在直角△AEF中,∵∠AEF=90°,∠AFE=39.3°+45°=84.3°, ∴AE=EF•tan∠AFE≈×10.02=18.036(米). 在直角△ABE中,∵∠ABE=90°,∠AEB=45°, ∴AB=AE•sin∠AEB≈18.036×≈18(米). 故旗杆AB的高度约为18米. 20.(10分)如图,⊙O为锐角△ABC的外接圆,半径为5. (1)用尺规作图作出∠BAC的平分线,并标出它与劣弧的交点E(保留作图痕迹,不写作法); (2)若(1)中的点E到弦BC的距离为3,求弦CE的长. 【分析】(1)利用基本作图作AE平分∠BAC; (2)连接OE交BC于F,连接OC,如图,根据圆周角定理得到=,再根据垂径定理得到OE⊥BC,则EF=3,OF=2,然后在Rt△OCF中利用勾股定理计算出CF=,在Rt△CEF中利用勾股定理可计算出CE. 【解答】解:(1)如图,AE为所作; (2)连接OE交BC于F,连接OC,如图, ∵AE平分∠BAC, ∴∠BAE=∠CAE, ∴=, ∴OE⊥BC, ∴EF=3, ∴OF=5﹣3=2, 在Rt△OCF中,CF==, 在Rt△CEF中,CE==. 六、解答题(本大题满分12分) 21.(12分)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下: (1)本次比赛参赛选手共有 50 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 30% ; (2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由; (3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率. 【分析】(1)用“59.5~69.5”这组的人数除以它所占的百分比可得到调查的总人数;再计算出“89.5~99.5”这一组人数占总参赛人数的百分比,然后用1分别减去其它三组的百分比得到“69.5~79.5”这一组人数占总参赛人数的百分比; (2)利用“59.5~69.5”和“69.5~79.5”两分数段的百分比为40%可判断他不能获奖; (3)画树状图展示所有12种等可能的结果数,再找出恰好选中1男1女的结果数,然后根据概率公式求解. 【解答】解:(1)5÷10%=50, 所以本次比赛参赛选手共有50人, “89.5~99.5”这一组人数占总参赛人数的百分比为×100%=24%, 所以“69.5~79.5”这一组人数占总参赛人数的百分比为1﹣10%﹣36%﹣24%=30%; 故答案为50,30%; (2)他不能获奖. 理由如下: 他的成绩位于“69.5~79.5”之间, 而“59.5~69.5”和“69.5~79.5”两分数段的百分比为10%+30%=40%, 因为成绩由高到低前60%的参赛选手获奖,他位于后40%, 所以他不能获奖; (3)画树状图为: 共有12种等可能的结果数,其中恰好选中1男1女的结果数为8, 所以恰好选中1男1女的概率==. 七、解答题(本题满分12分) 22.(12分)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现: ①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元; ②花卉的平均每盆利润始终不变. 小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元). (1)用含x的代数式分别表示W1,W2; (2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少? 【分析】(1)设培植的盆景比第一期增加x盆,则第二期盆景有(50+x)盆,花卉有(50﹣x)盆,根据“总利润=盆数×每盆的利润”可得函数解析式; (2)将盆景的利润加上花卉的利润可得总利润关于x的函数解析式,配方成顶点式,利用二次函数的性质求解可得. 【解答】解:(1)设培植的盆景比第一期增加x盆, 则第二期盆景有(50+x)盆,花卉有(50﹣x)盆, 所以W1=(50+x)(160﹣2x)=﹣2x2+60x+8000, W2=19(50﹣x)=﹣19x+950; (2)根据题意,得: W=W1+W2 =﹣2x2+60x+8000﹣19x+950 =﹣2x2+41x+8950 =﹣2(x﹣)2+, ∵﹣2<0,且x为整数, ∴当x=10时,W取得最大值,最大值为9160, 答:当x=10时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是9160元. 八、解答题(本题满分14分) 23.(14分)如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E.点M为BD中点,CM的延长线交AB于点F. (1)求证:CM=EM; (2)若∠BAC=50°,求∠EMF的大小; (3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM. 【分析】(1)利用直角三角形斜边中线的性质定理即可证明; (2)利用四边形内角和定理求出∠CME即可解决问题; (3)首先证明△ADE是等腰直角三角形,△DEM是等边三角形,设FM=a,则AE=CM=EM=a,EF=2a,推出=,=,由此即可解决问题; 【解答】(1)证明:如图1中, ∵DE⊥AB, ∴∠DEB=∠DCB=90°, ∵DM=MB, ∴CM=DB,EM=DB, ∴CM=EM. (2)解:∵∠AED=90°,∠A=50°, ∴∠ADE=40°,∠CDE=140°, ∵CM=DM=ME, ∴∠MCD=∠MDC,∠MDE=∠MED, ∴∠CME=360°﹣2×140°=80°, ∴∠EMF=180°﹣∠CME=100°. (3)证明:如图2中,设FM=a. ∵△DAE≌△CEM,CM=EM, ∴AE=ED=EM=CM=DM,∠AED=∠CME=90° ∴△ADE是等腰直角三角形,△DEM是等边三角形, ∴∠DEM=60°,∠MEF=30°, ∴AE=CM=EM=a,EF=2a, ∵CN=NM, ∴MN=a, ∴=,=, ∴=, ∴EM∥AN. 查看更多