2020高考数学一轮复习 函数系列之指数函数、对数函数学案(无答案)
指数函数、对数函数
知识梳理
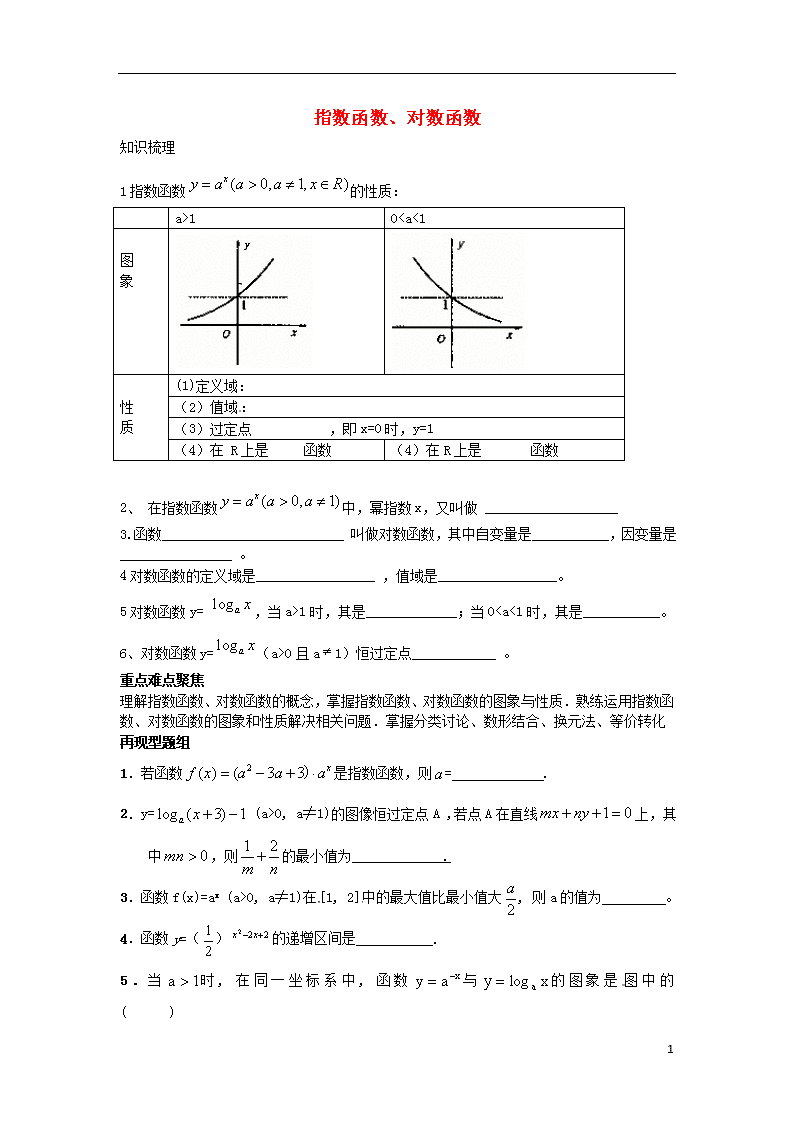
1指数函数的性质:
a>1
0
1时,其是_____________;当00且a1)恒过定点____________ 。
重点难点聚焦
理解指数函数、对数函数的概念,掌握指数函数、对数函数的图象与性质.熟练运用指数函数、对数函数的图象和性质解决相关问题.掌握分类讨论、数形结合、换元法、等价转化
再现型题组
1.若函数是指数函数,则= .
2.y= (a>0, a≠1)的图像恒过定点A ,若点A在直线上,其中,则的最小值为 .
3.函数f(x)=ax (a>0, a≠1)在[1, 2]中的最大值比最小值大, 则a的值为 。
4.函数y=()的递增区间是___________.
5.当时, 在同一坐标系中, 函数与的图象是图中的 ( )
3
6.设,,,则( )
A. B. C. D.
巩固型题组
7. 已知,求的值域及单调区间.
8.已知,求函数的最大值和最小值.
9. 已知a>0 , a≠1,
(1)当f(x)的定义域为(-1,1)时,解关于m的不等式f(1-m)+f(1-m2)<0;
(2)若f(x)-4恰在(-∞,2)上取负值,求a的值
3
反馈型题组
10.若函数的图象与x轴有公共点,则m的取值范围是( )
A.m≤-1 B.-1≤m<0 C.m≥1 D.01,则a的取值范围是 ( )
A.或 B.或
C. D.或
12.函数,x1,x2∈R且x1≠x2,则 ( )
A. B.
C. D.以上答案都不对
13.下图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图象,则a、b、c、d与1的大小关系是 ( )
A.a<b<1<c<d B.b<a<1<d<c
C.1<a<b<c<d D.a<b<1<d<c
14.若函数的图象过第一、三、四象限,则应满足 .
15. 设函数f(x)=lg(x+ax-a-1),给出下述命题:⑴f(x)有最小值;⑵当a=0时,f(x)的值域为R;⑶当a=0时,f(x)为偶函数;⑷若f(x)在区间[2,+)上单调递增,则实数a的取范围是a≥-4.则其中正确命题的序号 .
16. 已知函数,当a
查看更多