- 2023-06-24 发布 |
- 37.5 KB |
- 23页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学中考复习课件章节考点专题突破:第七章 图形变化考点突破34锐角三角函数和解直角三角形
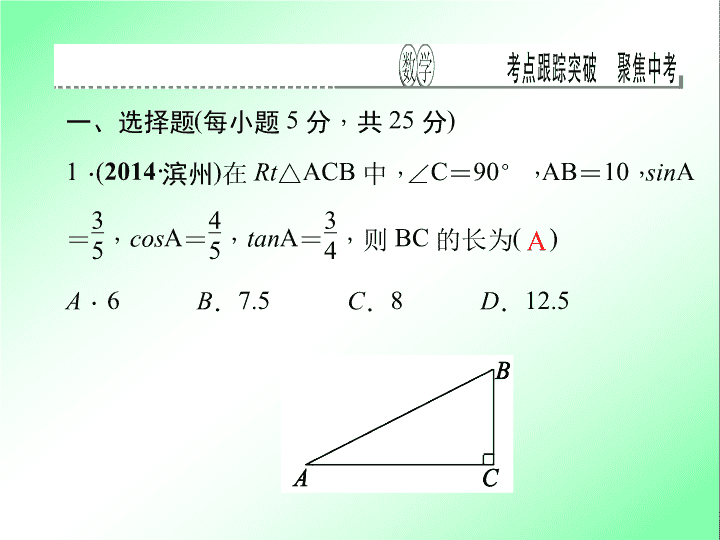
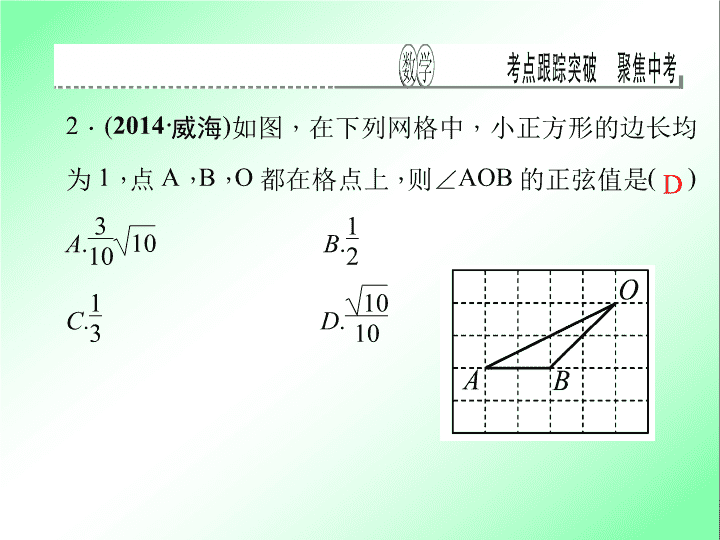
考点跟踪突破 34 锐角三角函数和解直角三角形 一、选择题 ( 每小题 5 分 , 共 25 分 ) 1 . ( 2014· 滨州 ) 在 Rt △ ACB 中 , ∠ C = 90 ° , AB = 10 , sin A = 3 5 , cos A = 4 5 , tan A = 3 4 , 则 BC 的长为 ( ) A . 6 B . 7.5 C . 8 D . 12.5 A 2 . ( 2014· 威海 ) 如图 , 在下列网格中 , 小正方形的边长均 为 1 , 点 A , B , O 都在格点上 , 则 ∠ AOB 的正弦值是 ( ) A . 3 10 10 B . 1 2 C . 1 3 D . 10 10 D 3 . ( 2014· 凉山州 ) 在 △ ABC 中 , 若 | cos A - 1 2 | + ( 1 - tan B ) 2 = 0 , 则 ∠ C 的度数是 ( ) A . 45 ° B . 60 ° C . 75 ° D . 105 ° C 4 . ( 2014· 苏州 ) 如图 , 港口 A 在观测站 O 的正东方向 , OA = 4 km , 某船从港口 A 出发 , 沿北偏东 15 ° 方向航行 一段距离后到达 B 处 , 此时从观测站 O 处测得该船位于 北偏东 60 ° 的方向 , 则该船航行的距离 ( 即 AB 的长 ) 为 ( ) A . 4 km B . 2 3 km C . 2 2 km D . ( 3 + 1 ) km C 5 . ( 2014· 德州 ) 如图是拦水坝的横断面 , 斜坡 AB 的水平 宽度为 12 米 , 斜面坡度为 1 ∶ 2 , 则斜坡 AB 的长为 ( ) A . 4 3 米 B . 6 5 米 C . 12 5 米 D . 24 米 B 二、填空题 ( 每小题 5 分 , 共 25 分 ) 6 . ( 2014· 温州 ) 如图 , 在 △ ABC 中 , ∠ C = 90 ° , AC = 2 , BC = 1 , 则 tan A 的值是 __ __ . 7 . ( 2013· 安顺 ) 在 Rt △ ABC 中 , ∠ C = 90 ° , tan A = 4 3 , BC = 8 , 则 △ ABC 的面积为 __ __ . 24 8 . ( 2013· 杭州 ) 在 Rt △ ABC 中 , ∠ C = 90 ° , AB = 2BC , 现给出下列结论: ① sin A = 3 2 ; ② cos B = 1 2 ; ③ tan A = 3 3 ; ④ tan B = 3 . 其中正确的是 . ( 填序号 ) ②③④ 9 . ( 2014 · 舟山 ) 如图 , 在地面上的点 A 处测得树顶 B 的仰角为 α 度 , AC = 7 米 , 则树高 BC 为 米. ( 用含 α 的代数式表示 ) 7 tan α 10 . ( 2014· 宁波 ) 为解决停车难的问题 , 在如图一段长 56 米的路段开辟停车位 , 每个车位是长 5 米宽 2.2 米的矩形 , 矩形的边与路的边缘成 45 ° 角 , 那么这个路段最多可以 划出 ____ 个这样的停车位. ( 2 ≈ 1.4) 17 三、解答题 ( 共 50 分 ) 11 . ( 10 分 ) ( 2014· 内江 ) “ 马航事件 ” 的发生引起了我国政府的高度 重视 , 迅速派出了舰船和飞机到相关海域进行搜寻 . 如图 , 在一次 空中搜寻中 , 水平飞行的飞机观测得在点 A 俯角为 30 ° 方向的 F 点处有疑似飞机残骸的物体 ( 该物体视为静止 ) . 为了便于观察 , 飞 机继续向前飞行了 800 米到达 B 点 , 此时测得点 F 在点 B 俯角为 45 ° 的方向上 , 请你计算当飞机飞临 F 点的正上方点 C 时 ( 点 A , B , C 在同一直线上 ) , 竖直高度 CF 约为多少米? ( 结果保留整数 , 参考 数值: 3 ≈ 1.7 ) 解: ∵ ∠ BCF = 90 ° , ∠ FBC = 45 ° , ∴ BC = CF , ∵∠ CAF = 30 ° , ∴ tan 30 ° = CF AB + BC = CF CF + AB = CF 800 + CF = 3 3 , 解 得 CF = 400 3 + 400 ≈ 400 × ( 1.7 + 1 ) = 1 080 ( 米 ) . 答:竖直高 度 CF 约为 1 080 米 12 . (10 分 ) ( 2014 · 宁波 ) 如图 , 从 A 地到 B 地的公路需经过 C 地 , 图中 AC = 10 千米 , ∠ CAB = 25° , ∠ CBA = 37° , 因城市规划的需要 , 将在 A , B 两地之间修建一条笔直的公路. (1) 求改直的公路 AB 的长; 解: (1) 作 CH ⊥ AB 于点 H. 在 Rt △ ACH 中 , CH = AC · sin ∠ CAB = AC· sin 25° ≈ 10 × 0.42 = 4.2 千米 , AH = AC · cos ∠ CAB = AC · cos 25° ≈ 10 × 0.91 = 9.1 千米 , 在 Rt △ BCH 中 , BH = CH÷ tan ∠ CBA = 4.2÷ tan 37° ≈ 4.2÷0.75 = 5.6 千米 , ∴ AB = AH + BH = 9.1 + 5.6 = 14.7 千米.故改直的公路 AB 的长 14.7 千米 (2) 问公路改直后比原来缩短了多少千米? ( sin 25° ≈ 0.42 , cos 25° ≈ 0.91 , sin 37° ≈ 0.60 , tan 37° ≈ 0.75) (2) 在 Rt △ BCH 中 , BC = CH÷ sin ∠ CBA = 4.2÷ sin 37° ≈ 4.2÷0.6 = 7 千米 , 则 AC + BC - AB = 10 + 7 - 14.7 = 2.3 千米.答:公路改直后比原来缩短了 2.3 千米 13 . (10 分 ) ( 2014· 遵义 ) 如图 , 一楼房 AB 后有一假山 , 其坡度 为 i = 1 ∶ 3 , 山坡坡面上 E 点处有一休息亭 , 测得假山坡脚 C 与楼房水平距离 BC = 25 米 , 与亭子距离 CE = 20 米 , 小丽从 楼房顶测得 E 点的俯角为 45 ° , 求楼 房 AB 的高. ( 注:坡度 i 是指坡面的铅直高度与水平宽度的比 ) 解: 解:过点 E 作 EF ⊥ BC 的延长线于点 F , EH ⊥ AB 于点 H , 在 Rt △ CEF 中 , ∵ i = EF CF = 1 3 = tan ∠ ECF , ∴∠ ECF = 30 ° , ∴ EF = 1 2 CE = 10 米 , CF = 10 3 米 , ∴ BH = EF = 10 米 , HE = BF = BC + CF = (25 + 10 3 ) 米 , 在 Rt △ AHE 中 , ∵∠ HAE = 45 ° , ∴ AH = HE = (25 + 10 3 ) 米 , ∴ AB = AH + HB = (35 + 10 3 ) 米. 答:楼房 AB 的高为 (35 + 10 3 ) 米 14 . (10 分 ) ( 2013 · 绍兴 ) 如图 , 伞不论张开还是收紧 , 伞柄 AP 始终平分同一平面内两条伞架所成的角 ∠ BAC , 当伞收紧时 , 点 D 与点 M 重合 , 且点 A , E , D 在同一条直线上 , 已知部分伞架的长度如下: ( 单位: cm ) 伞架 DE DF AE AF AB AC 长度 36 36 36 36 86 86 (1) 求 AM 的长; (2) 当 ∠ BAC = 104° 时 , 求 AD 的长. ( 精确到 1 cm ) 备用数据: sin 52° ≈ 0.7880 , cos 52° ≈ 0.6157 , tan 52° ≈ 1.2799. 解: (1) 由题意 , 得 AM = AE + DE = 36 + 36 = 72 ( cm ) .故 AM 的长为 72 cm (2) ∵ AP 平分 ∠ BAC , ∠ BAC = 104 ° , ∴∠ EAD = 1 2 ∠ BAC = 52 ° . 过点 E 作 EG ⊥ AD 于点 G , ∵ AE = DE = 36 , ∴ AG = DG , AD = 2AG. 在 △ AEG 中 , ∵∠ AGE = 90 ° , ∴ AG = AE· cos ∠ EAG = 36· cos 52 ° = 36 × 0.615 7 = 22.165 2 , ∴ AD = 2AG = 2 × 22.165 2 ≈ 44 ( cm ) . 故 AD 的长约为 44 cm 15 . ( 10 分 ) ( 2013· 眉山 ) 如图 , 某防洪指挥部发现长江边一 处长 500 米 , 高 10 米 , 背水坡的坡角为 45 ° 的防洪大堤 ( 横断面为梯形 ABCD ) 急需加固 . 经调查论证 , 防洪指挥 部专家组制定的加固方案是:背水 坡面用土石进行加固 , 并使上底加宽 3 米 , 加固后背水坡 EF 的坡比 i = 1 ∶ 3 . (1) 求加固后坝底增加的宽度 AF ; (2) 求完成这项工程需要土石多少立方米? ( 结果保留根号 )查看更多