2020八年级数学上册 专题突破讲练 解密最短距离之建桥选址试题 （新版）青岛版

2020八年级数学上册 专题突破讲练 解密最短距离之建桥选址试题 （新版）青岛版

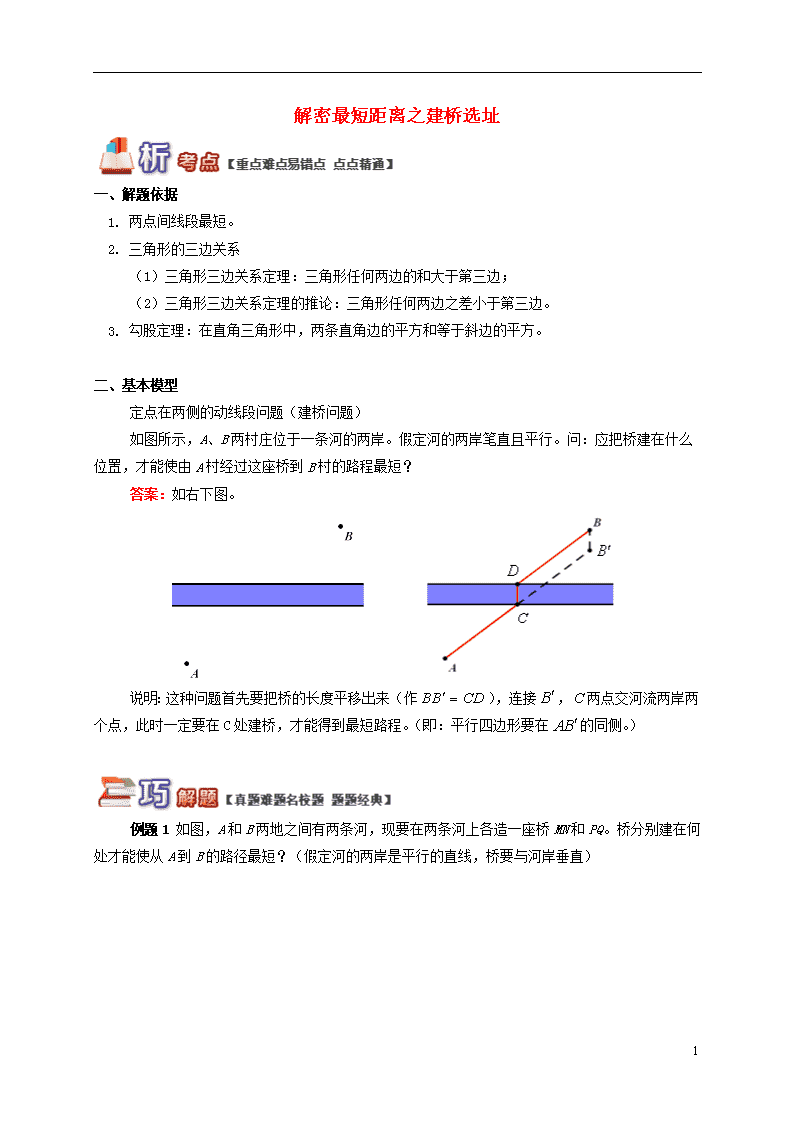
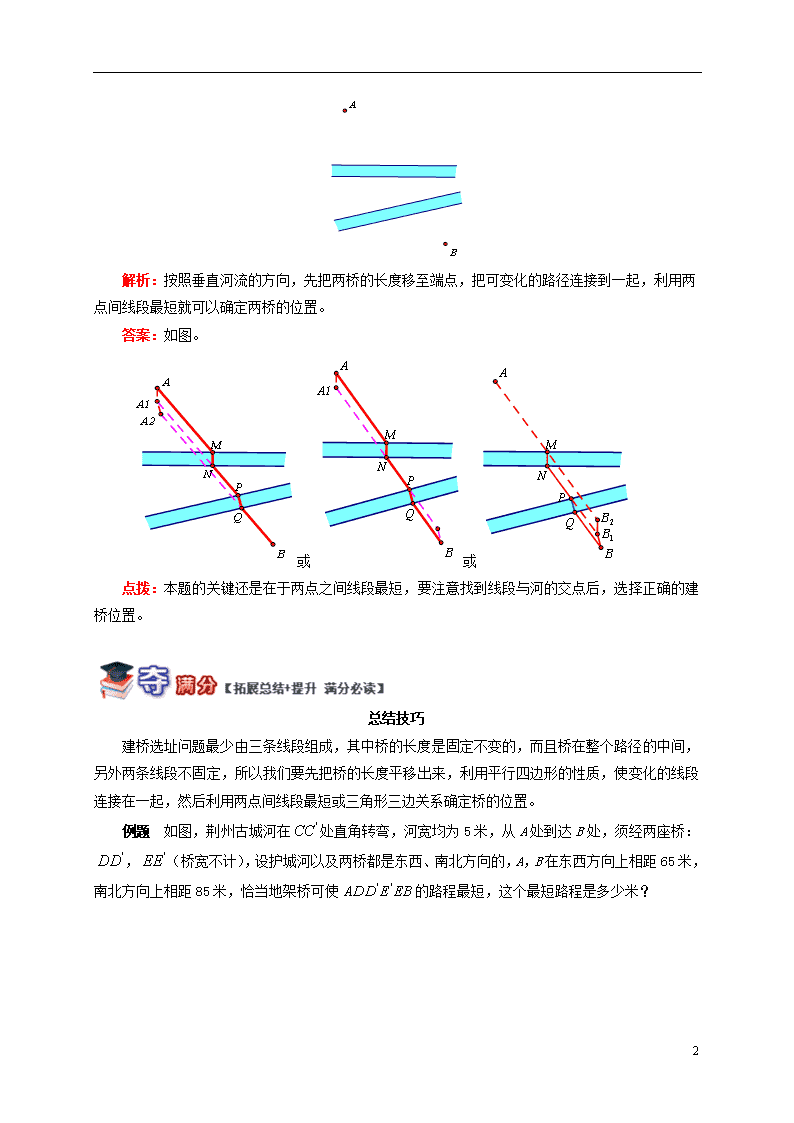
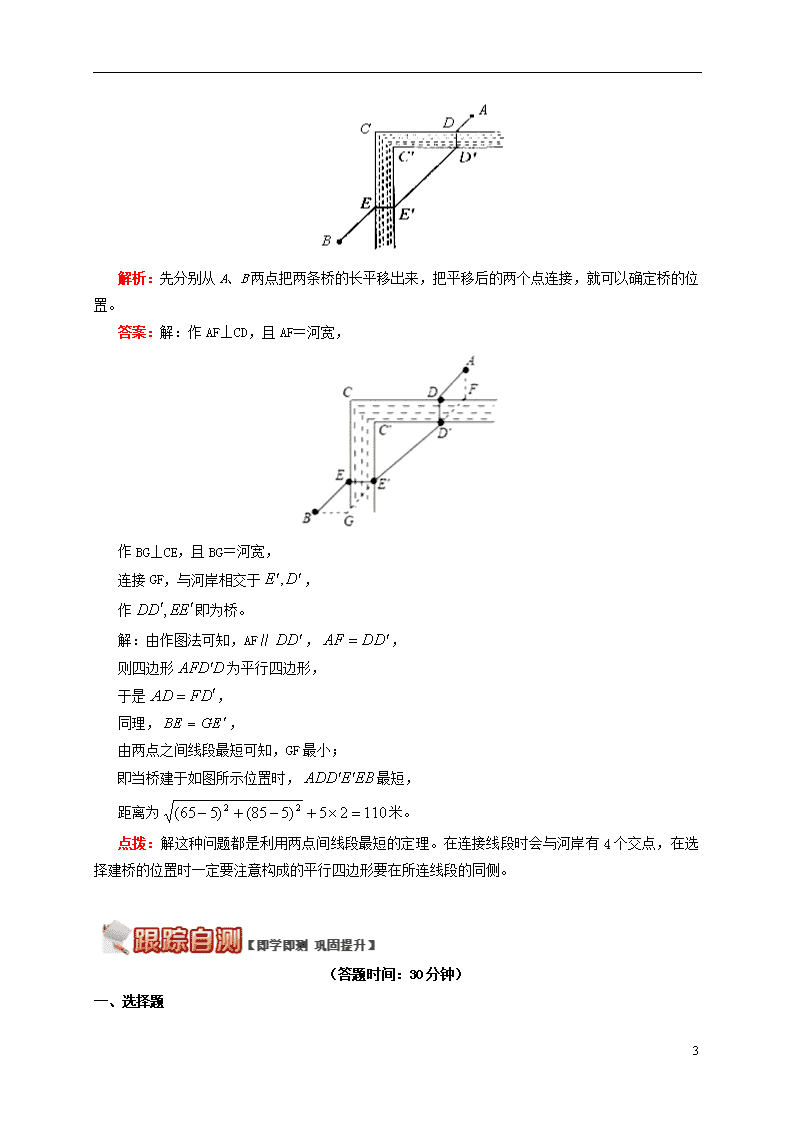
解密最短距离之建桥选址 一、解题依据 ‎1. 两点间线段最短。‎ ‎2. 三角形的三边关系 ‎（1）三角形三边关系定理：三角形任何两边的和大于第三边；‎ ‎（2）三角形三边关系定理的推论：三角形任何两边之差小于第三边。‎ ‎3. 勾股定理：在直角三角形中，两条直角边的平方和等于斜边的平方。‎ 二、基本模型 定点在两侧的动线段问题（建桥问题）‎ 如图所示，A、B两村庄位于一条河的两岸。假定河的两岸笔直且平行。问：应把桥建在什么位置，才能使由A村经过这座桥到B村的路程最短？‎ 答案：如右下图。‎ ‎ ‎ 说明：这种问题首先要把桥的长度平移出来（作），连接，两点交河流两岸两个点，此时一定要在C处建桥，才能得到最短路程。（即：平行四边形要在的同侧。）‎ 例题1 如图，A和B两地之间有两条河，现要在两条河上各造一座桥MN和PQ。桥分别建在何处才能使从A到B的路径最短？（假定河的两岸是平行的直线，桥要与河岸垂直）‎ 9‎ 解析：按照垂直河流的方向，先把两桥的长度移至端点，把可变化的路径连接到一起，利用两点间线段最短就可以确定两桥的位置。‎ 答案：如图。‎ 或或 点拨：本题的关键还是在于两点之间线段最短，要注意找到线段与河的交点后，选择正确的建桥位置。‎ 总结技巧 建桥选址问题最少由三条线段组成，其中桥的长度是固定不变的，而且桥在整个路径的中间，另外两条线段不固定，所以我们要先把桥的长度平移出来，利用平行四边形的性质，使变化的线段连接在一起，然后利用两点间线段最短或三角形三边关系确定桥的位置。‎ 例题 如图，荆州古城河在处直角转弯，河宽均为‎5米，从A处到达B处，须经两座桥：，（桥宽不计），设护城河以及两桥都是东西、南北方向的，A，B在东西方向上相距‎65米，南北方向上相距‎85米，恰当地架桥可使的路程最短，这个最短路程是多少米？‎ 9‎ 解析：先分别从A、B两点把两条桥的长平移出来，把平移后的两个点连接，就可以确定桥的位置。‎ 答案：解：作AF⊥CD，且AF＝河宽，‎ 作BG⊥CE，且BG＝河宽，‎ 连接GF，与河岸相交于，‎ 作即为桥。‎ 解：由作图法可知，AF∥，，‎ 则四边形为平行四边形，‎ 于是，‎ 同理，，‎ 由两点之间线段最短可知，GF最小；‎ 即当桥建于如图所示位置时，最短，‎ 距离为米。‎ 点拨：解这种问题都是利用两点间线段最短的定理。在连接线段时会与河岸有4个交点，在选择建桥的位置时一定要注意构成的平行四边形要在所连线段的同侧。‎ ‎（答题时间：30分钟）‎ 一、选择题 9‎ ‎1. 如图，A和B两地在一条河的两岸，现要在河上造一座桥MN，使从A到B的路径AMNB最短的是（假定河的两岸是平行直线，桥要与河岸垂直）（　　）‎ A. ‎ B. ‎ C. ‎ D.‎ ‎2.（荔城区二模）如图，在边长为10的菱形ABCD中，对角线BD＝16。点E是AB的中点，P、Q是BD上的动点，且始终保持PQ＝2。则四边形AEPQ周长的最小值为（ ）。（结果保留根号）‎ A. B. C. D. ‎ 二、填空题 ‎3.（山西模拟）如图，已知四边形ABCD四个顶点的坐标为A（1，3），B（m，0），C（m＋2，0），D（5，1），当四边形ABCD的周长最小时，m的值为 。‎ ‎4.（峨边县模拟）如图，A（1，－3），B（4，－1），P（a，0），N（a＋2，0），当四边形ABNP的周长最小时，a＝_______。‎ 9‎ 三、解答题 ‎5. 如图，A和B两地之间有三条河，现要在三条河上各造一座桥MN、PQ和GH。桥分别建在何处才能使从A到B的路径最短？（假定河的两岸是平行的直线，桥要与河岸垂直）‎ ‎**6. 五羊大学建立分校，校本部与分校隔着两条平行的小河，如图表示小河甲，表示小河乙，A为校本部大门，B为分校大门。为方便人员往来，要在两条小河上各建一条桥，桥面垂直于河岸。图中的尺寸是：甲河宽‎8米，乙河宽‎10米，A到甲河的垂直距离为‎40米，B到乙河的垂直距离为‎20米，两河相距‎100米，A、B两点的水平距离（与小河平行的方向）为‎120米。为使A、B两点间来往的路程最短，两条桥都按这个目标而建，那么此时A、B两点来往的路程是多少米？‎ ‎7. 如图，如果A、B之间有三条平行的河流，试确定桥的位置，使所走路径最短。 ‎ 9‎ 9‎ ‎1. D 解析：由基本模型可知，AM∥BN。‎ ‎2. B 解析：将菱形ABCD放置在平面直角坐标系中，使得B为原点，BD在x轴的正半轴上，‎ 根据题意得出A、B、E三点的坐标，A（8，6）、B（0，0）、E（4，3）。‎ 将A平行向左移动2个单位到A'点，则（6，6），‎ 作A'关于x轴的对称点F，则F（6，－6），‎ 连EF，交x轴于点P，在x轴的正方向上截取PQ＝2，‎ 此时四边形AEPQ的周长最小，‎ AQ＋EP＝A'P＋EP＝FP＋EP＝EF，由此即可得出结论。‎ ‎3. 解析：将点D向左平移2个单位到D′（3，1），作D′关于x轴的对称点D″，根据作法知点D″（3，－1），‎ 设直线AD″的解析式为y＝kx＋b，‎ 则，‎ 解得k＝－2，b＝5。‎ ‎∴直线AD″的解析式为y＝－2x＋5。‎ 当y＝0时，x＝，即B（，0），m＝。‎ ‎4. 解析：点B向左平移2个单位到B′（2，－1），作B′关于x轴的对称点B″，‎ 根据作法知点B″（2，1），连接AB″，交x轴于P，‎ 9‎ 设直线AB″的解析式为y＝kx＋b，‎ 则，解得。‎ ‎∴y＝4x－7。‎ 当y＝0时，x＝，‎ 即P（，0），a＝‎ ‎5. 或或 9‎ 或 ‎**6. ‎218米 解析：作图，由题意可知路程AMNPQB最短，且AMNPQB＝AD＋DC＋CB 又AD＝‎8米，CB＝‎10米，由已知条件可得CE＝‎120米，DE＝40＋20＋100＝‎160米，‎ 所以在Rt△DEC中可求得斜边CD＝‎200米，‎ 所以AD＋DC＋CB＝8＋200＋10＝‎218米。‎ ‎7. 解：将点A沿与河垂直的方向平移三个河宽分别到A1、A2、A3，路径中三座桥的长度是固定的。为了使路径最短，只要A3B最短。连接A3B，交河流3于N，在此处造桥MN；连接A‎2M，交河流2于P，在此处造桥PQ；连接A1Q，交河流1于R，在此处造桥RS。所得路径ASRQPMNB最短。‎ 9‎