- 2023-06-07 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020中考数学复习基础小卷速测十等边腰三角形相关计算与证明
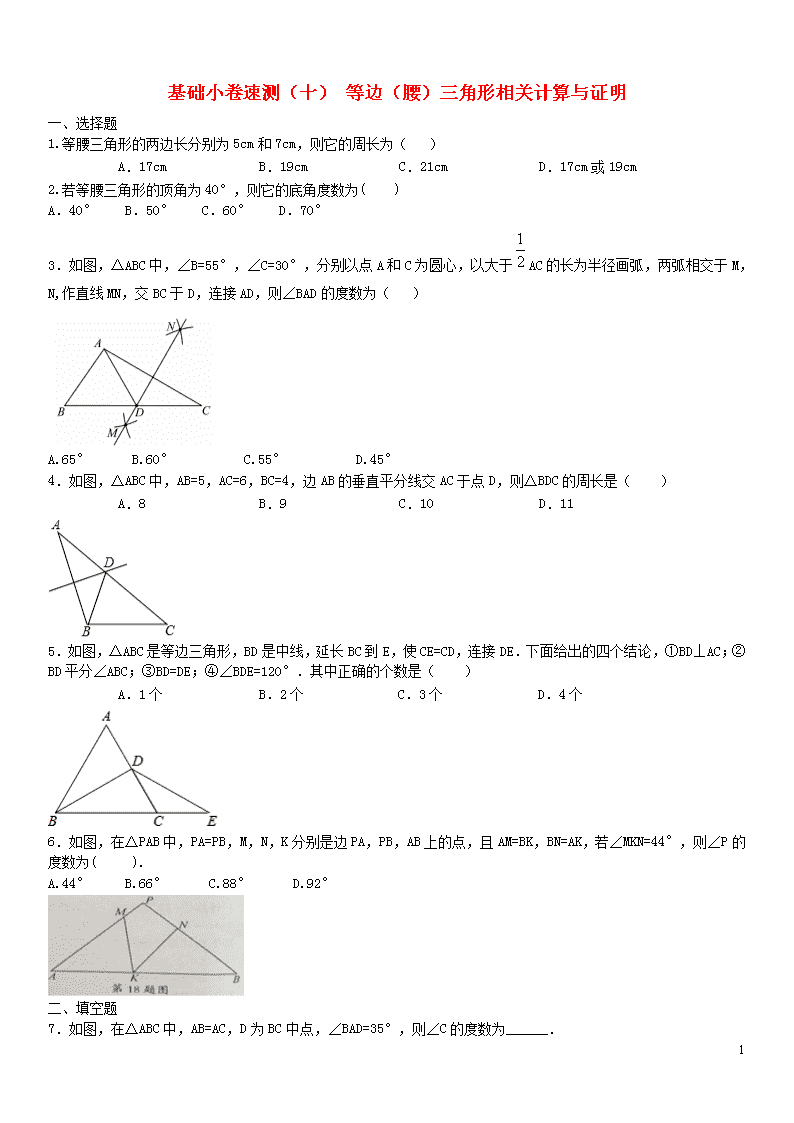
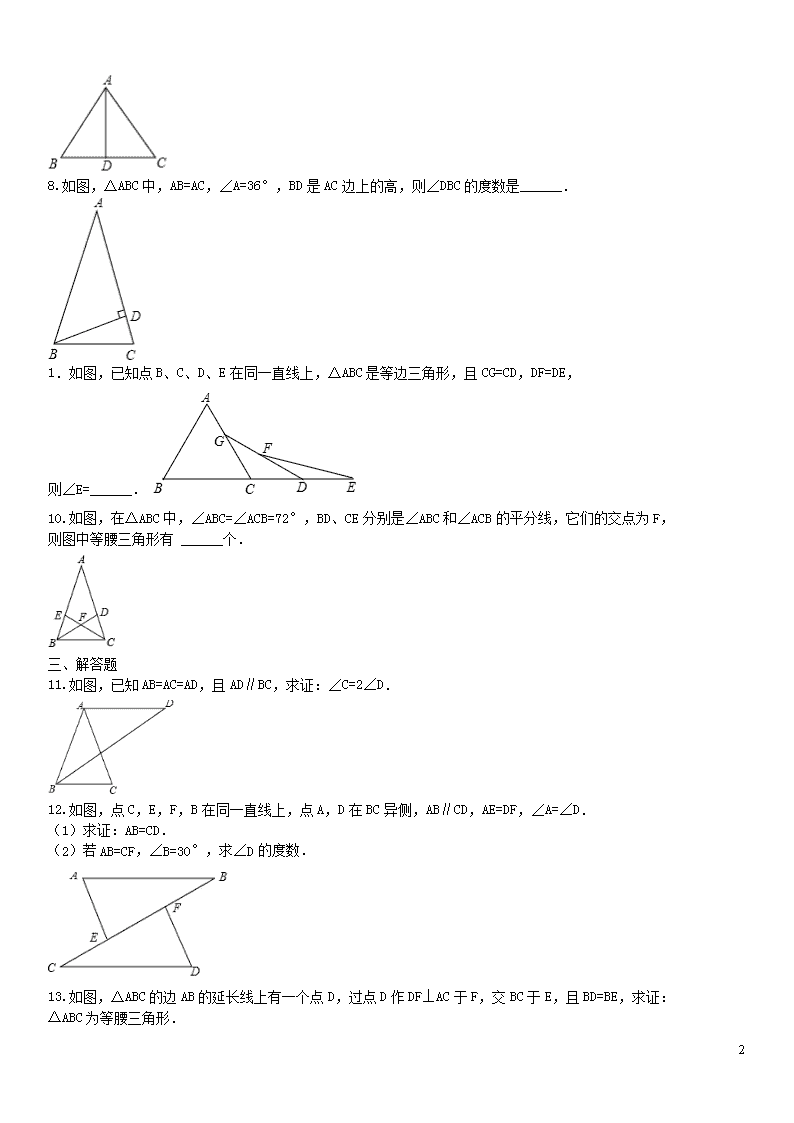
基础小卷速测(十) 等边(腰)三角形相关计算与证明 一、选择题 1.等腰三角形的两边长分别为5cm和7cm,则它的周长为( ) A.17cm B.19cm C.21cm D.17cm或19cm 2.若等腰三角形的顶角为40°,则它的底角度数为( ) A.40° B.50° C.60° D.70° 3.如图,△ABC中,∠B=55°,∠C=30°,分别以点A和C为圆心,以大于AC的长为半径画弧,两弧相交于M,N,作直线MN,交BC于D,连接AD,则∠BAD的度数为( ) A.65° B.60° C.55° D.45° 4.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( ) A.8 B.9 C.10 D.11 5.如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,连接DE.下面给出的四个结论,①BD⊥AC;②BD平分∠ABC;③BD=DE;④∠BDE=120°.其中正确的个数是( ) A.1个 B.2个 C.3个 D.4个 6.如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( ). A.44° B.66° C.88° D.92° 二、填空题 7.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为______. 5 8.如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是______. 1. 如图,已知点B、C、D、E在同一直线上,△ABC是等边三角形,且CG=CD,DF=DE, 则∠E=______. 10.如图,在△ABC中,∠ABC=∠ACB=72°,BD、CE分别是∠ABC和∠ACB的平分线,它们的交点为F, 则图中等腰三角形有 ______个. 三、解答题 11.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D. 12.如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D. (1)求证:AB=CD. (2)若AB=CF,∠B=30°,求∠D的度数. 13.如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,求证: △ABC为等腰三角形. 5 14.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,且PD∥AB,PE∥AC,BC=5,求△PDE的周长. 15.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上. 求证:(1)CE=AC+DC;(2)∠ECD=60°. 参考答案 1. D 2.D 3.A 4.C 【解析】∵ED是AB的垂直平分线,∴AD=BD, ∵△BDC的周长=DB+BC+CD,∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10. 5.D 【解析】∵△ABC是等边三角形,BD是AC上的中线, ∴∠ADB=∠CDB=90°,BD平分∠ABC, ∴BD⊥AC, ∵∠ACB=∠CDE+∠DEC=60°,CD=CE, ∴∠CDE=∠DEC=30°, ∴∠CBD=∠DEC, ∴DB=DE. ∠BDE=∠CDB+∠CDE=120°. 所以这四项都是正确的. 6.D【解析】∵PA=PB,∴∠A=∠B, 在△AMK和△BKN中, ∴△AMK≌△BKN,∴∠AMK=∠BKN, ∵∠MKB=∠MKN+∠NKB=∠A+∠AMK, ∴∠A=∠MKN=44°, ∴∠P=180°-∠A-∠B=92°。 5 7.55°【解析】AB=AC,D为BC中点, ∴AD是∠BAC的平分线,∠B=∠C, ∵∠BAD=35°, ∴∠BAC=2∠BAD=70°, ∴∠C=(180°-70°)=55°。 8. 18°【解析】∵AB=AC,∠A=36°, ∴∠ABC=∠ACB=72°, ∵BD是AC边上的高, ∴BD⊥AC, ∴∠DBC=90°-72°=18°。 9. 15°【解析】∵△ABC是等边三角形, ∴∠ACB=60°,∠ACD=120°, ∵CG=CD, ∴∠CDG=30°,∠FDE=150°, ∵DF=DE, ∴∠E=15°. 10. 8【解析】∠ABD=∠DBC=∠ECB=∠ACE=∠A=36°, ∠ABC=∠ACB=∠CDB=∠CFD=∠BFE=∠BEF=72°, ∴△ABC,△ABD,△ACE,△BEF,△CDF,△BCF,△BCE,△BCD均为等腰三角形, ∴共有8个等腰三角形. 11.证明:∵AB=AC=AD, ∴∠C=∠ABC,∠D=∠ABD, ∴∠ABC=∠CBD+∠D, ∵AD∥BC, ∴∠CBD=∠D, ∴∠ABC=∠D+∠D=2∠D, 又∵∠C=∠ABC, ∴∠C=2∠D. 12.解:(1)证明:∵AB∥CD, ∴∠B=∠C, 在△ABE和△CDF中, ∴△ABE≌△CDF(AAS), ∴AB=CD。 (2)∵△ABE≌△CDF, ∴AB=CD,BE=CF, ∵AB=CF,∠B=30°, ∴AB=BE, ∴△ABE是等腰三角形, ∴∠D=×(180°−30°)=75°. 5 13.证明:∵DF⊥AC, ∴∠DFA=∠EFC=90°, ∴∠A=90°-∠D,∠C=90°-∠CEF, ∵BD=BE, ∴∠BED=∠D. ∵∠BED=∠CEF, ∴∠D=∠CEF. ∴∠A=∠C. ∴△ABC为等腰三角形. 14.解:∵BP平分∠ABC,CP平分∠ACB, ∴∠ABP=∠PBD,∠ACP=∠PCE, 又∵PD∥AB,PE∥AC, ∴∠ABP=∠BPD,∠ACP=∠CPE, ∴∠PBD=∠BPD,∠PCE=∠CPE, ∴BD=PD,CE=PE, ∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5. 1. 证明:(1)∵△ABC、△ADE是等边三角形, ∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°, ∴∠BAC+∠CAD=∠DAE+∠CAD, 即∠BAD=∠CAE, ∴△BAD≌△CAE, ∴BD=EC, ∵BD=BC+CD=AC+CD, ∴CE=BD=AC+CD。 (2)由(1)知△BAD≌△CAE, ∴∠ACE=∠ABD=60°, ∴∠ECD=180°-∠ACB-∠ACE=60°, ∴∠ECD=60°. 5查看更多