2020版高考数学大一轮复习 第七章 数列与数学归纳法 第5节 直接证明与间接证明(供选用)学案 理
第5节 直接证明与间接证明(供选用)
最新考纲 1.了解直接证明的两种基本方法——分析法和综合法;了解分析法和综合法的思考过程和特点;2.了解间接证明的一种基本方法——反证法;了解反证法的思考过程和特点.
知 识 梳 理
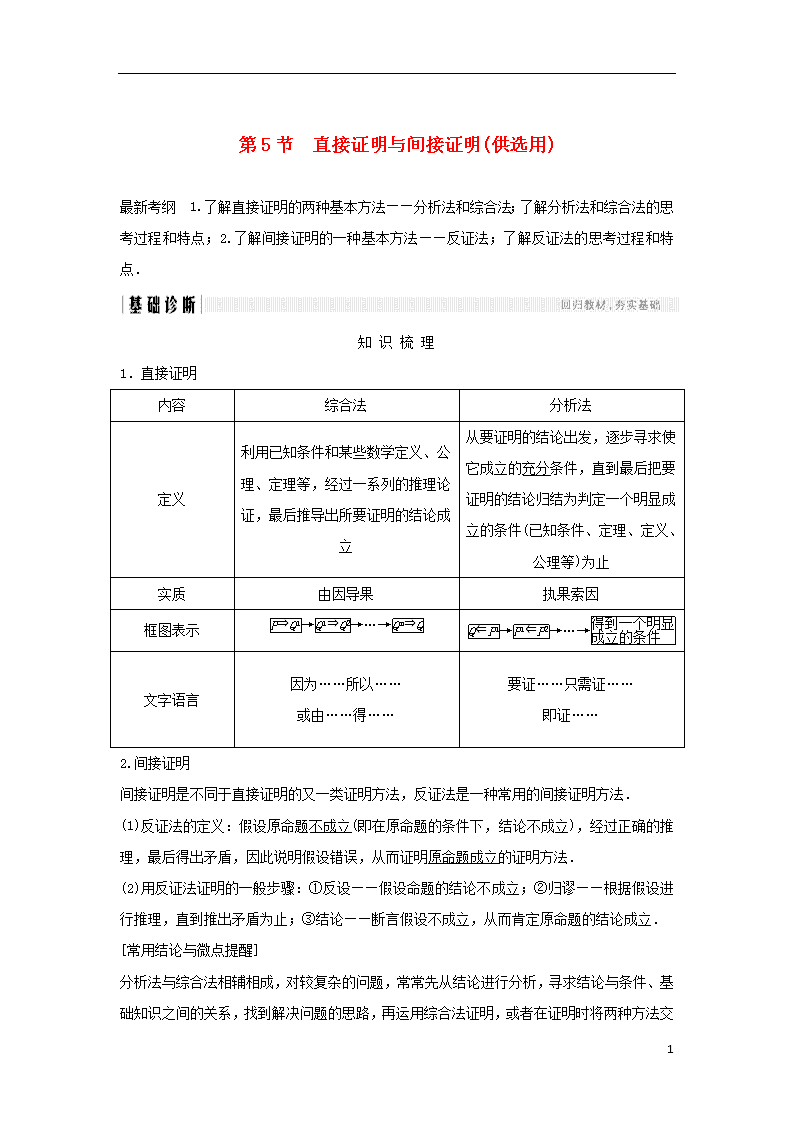
1.直接证明
内容
综合法
分析法
定义
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立
从要证明的结论出发,逐步寻求使它成立的充分条件,直到最后把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止
实质
由因导果
执果索因
框图表示
→→…→
→→…→
文字语言
因为……所以……
或由……得……
要证……只需证……
即证……
2.间接证明
间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法.
(1)反证法的定义:假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立的证明方法.
(2)用反证法证明的一般步骤:①反设——假设命题的结论不成立;②归谬——根据假设进行推理,直到推出矛盾为止;③结论——断言假设不成立,从而肯定原命题的结论成立.
[常用结论与微点提醒]
分析法与综合法相辅相成,对较复杂的问题,常常先从结论进行分析,寻求结论与条件、
12
基础知识之间的关系,找到解决问题的思路,再运用综合法证明,或者在证明时将两种方法交叉使用.
诊 断 自 测
1.思考辨析(在括号内打“√”或“×”)
(1)分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件.( )
(2)用反证法证明结论“a>b”时,应假设“a
ab>b2
C.< D.>
解析 a2-ab=a(a-b),∵a0,∴a2>ab.①
又ab-b2=b(a-b)>0,∴ab>b2,②
由①②得a2>ab>b2.
答案 B
4.用反证法证明命题:“设a,b为实数,则方程x3+ax+b=0至少有一个实根”时,要做的假设是( )
A.方程x3+ax+b=0没有实根
12
B.方程x3+ax+b=0至多有一个实根
C.方程x3+ax+b=0至多有两个实根
D.方程x3+ax+b=0恰好有两个实根
解析 因为“方程x3+ax+b=0至少有一个实根”等价于“方程x3+ax+b=0的实根的个数大于或等于1”,所以要做的假设是“方程x3+ax+b=0没有实根”.
答案 A
5.在△ABC中,三个内角A,B,C的对边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列,则△ABC的形状为________.
解析 由题意2B=A+C,又A+B+C=π,∴B=,又b2=ac,由余弦定理得b2=a2+c2-2accos B=a2+c2-ac,
∴a2+c2-2ac=0,即(a-c)2=0,∴a=c,
∴A=C,∴A=B=C=,∴△ABC为等边三角形.
答案 等边三角形
6.(2017·绍兴检测)完成反证法证题的全过程.设a1,a2,…,a7是1,2,…,7的一个排列,求证:乘积p=(a1-1)·(a2-2)·…·(a7-7)为偶数.
证明:假设p为奇数,则a1-1,a2-2,…,a7-7均为奇数.因奇数个奇数之和为奇数,故有奇数=____________=____________=0.但0≠奇数,这一矛盾说明p为偶数.
解析 ∵a1-1,a2-2,…,a7-7均为奇数,∴(a1-1)+(a2-2)+…+(a7-7)也为奇数,即(a1+a2+…+a7)-(1+2+…+7)为奇数.又∵a1,a2,…,a7是1,2,…,7的一个排列,∴a1+a2+…+a7=1+2+…+7,故上式为0,∴奇数=(a1-1)+(a2-2)+…+(a7-7)=(a1+a2+…+a7)-(1+2+…+7)=0.
答案 (a1-1)+(a2-2)+…+(a7-7) (a1+a2+…+a7)-(1+2+…+7)
考点一 综合法的应用
【例1】 已知a,b,c>0,a+b+c=1.求证:
(1)++≤;
(2)++≥.
证明 (1)∵(++)2=(a+b+c)+2+2+2≤(a+b+c)+(a+b)+(b+c
12
)+(c+a)=3,
∴++≤.
(2)∵a>0,∴3a+1>0,
∴+(3a+1)≥2=4,
∴≥3-3a,同理得≥3-3b,≥3-3c,
以上三式相加得
4≥9-3(a+b+c)=6,
∴++≥.
规律方法 用综合法证题是从已知条件出发,逐步推向结论,综合法的适用范围:
(1)定义明确的问题,如证明函数的单调性、奇偶性、求证无条件的等式或不等式;
(2)已知条件明确,并且容易通过分析和应用条件逐步逼近结论的题型.在使用综合法证明时,易出现的错误是因果关系不明确,逻辑表达混乱.
【训练1】 设a,b,c均为正数,且a+b+c=1,证明:
(1)ab+bc+ac≤;
(2)++≥1.
证明 (1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac得
a2+b2+c2≥ab+bc+ca.由题设知(a+b+c)2=1,
即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤.
(2)因为a>0,b>0,c>0,
所以+b≥2a,+c≥2b,+a≥2c,
故+++(a+b+c)≥2(a+b+c),
即++≥a+b+c.所以++≥1.
考点二 分析法的应用
【例2】 已知a>0,证明:-≥a+-2.
12
证明 要证-≥a+-2,
只需证≥-(2-).
因为a>0,所以-(2-)>0,
所以只需证≥,
即2(2-)≥8-4,只需证a+≥2.
因为a>0,a+≥2显然成立,所以要证的不等式成立.
规律方法 (1)逆向思考是用分析法证题的主要思想,通过反推,逐步寻找使结论成立的充分条件.正确把握转化方向是使问题顺利获解的关键.
(2)证明较复杂的问题时,可以采用两头凑的办法,即通过分析法找出某个与结论等价(或充分)的中间结论,然后通过综合法证明这个中间结论,从而使原命题得证.
【训练2】 △ABC的三个内角A,B,C成等差数列,A,B,C的对边分别为a,b,c.
求证:+=.
证明 要证+=,
即证+=3也就是+=1,
只需证c(b+c)+a(a+b)=(a+b)(b+c),
需证c2+a2=ac+b2,
又△ABC三内角A,B,C成等差数列,故B=60°,
由余弦定理,得b2=c2+a2-2accos 60°,即b2=c2+a2-ac,
故c2+a2=ac+b2成立.
于是原等式成立.
考点三 反证法的应用
【例3】 等差数列{an}的前n项和为Sn,a1=1+,S3=9+3.
(1)求数列{an}的通项an与前n项和Sn;
(2)设bn=(n∈N*),求证:数列{bn}中任意不同的三项都不可能成为等比数列.
(1)解 由已知得解得d=2,
故an=2n-1+,Sn=n(n+).
12
(2)证明 由(1)得bn==n+.假设数列{bn}中存在三项bp,bq,br(p,q,r∈N*,且互不相等)成等比数列,则b=bpbr.即(q+)2=(p+)(r+).
∴(q2-pr)+(2q-p-r)=0.
∵p,q,r∈N*,∴
∴=pr,(p-r)2=0.
∴p=r,与p≠r矛盾.
∴数列{bn}中任意不同的三项都不可能成为等比数列.
规律方法 (1)当一个命题的结论是以“至多”、“至少”、“唯一”或以否定形式出现时,可用反证法来证,反证法关键是在正确的推理下得出矛盾,矛盾可以是与已知条件矛盾,与假设矛盾,与定义、公理、定理矛盾,与事实矛盾等.
(2)用反证法证明不等式要把握三点:①必须否定结论;②必须从否定结论进行推理;③推导出的矛盾必须是明显的.
【训练3】 (2017·郑州一中月考)已知a1+a2+a3+a4>100,求证:a1,a2,a3,a4中至少有一个数大于25.
证明 假设a1,a2,a3,a4均不大于25,即a1≤25,a2≤25,a3≤25,a4≤25,则a1+a2+a3+a4≤25+25+25+25=100,
这与已知a1+a2+a3+a4>100矛盾,故假设错误.
所以a1,a2,a3,a4中至少有一个数大于25.
基础巩固题组
一、选择题
1.用反证法证明命题:“三角形三个内角至少有一个不大于60°”时,应假设( )
A.三个内角都不大于60°
B.三个内角都大于60°
C.三个内角至多有一个大于60°
D.三个内角至多有两个大于60°
答案 B
2.若a,b∈R,则下面四个式子中恒成立的是( )
12
A.lg(1+a2)>0 B.a2+b2≥2(a-b-1)
C.a2+3ab>2b2 D.<
解析 在B中,∵a2+b2-2(a-b-1)=(a2-2a+1)+(b2+2b+1)=(a-1)2+(b+1)2≥0,
∴a2+b2≥2(a-b-1)恒成立.
答案 B
3.已知m>1,a=-,b=-,则以下结论正确的是( )
A.a>b B.a+>0(m>1),
∴<,即a40,∴+>2+.
答案 +>2+
8.用反证法证明命题“a,b∈R,ab可以被5整除,那么a,b中至少有一个能被5整除”,那么假设的内容是______________.
解析 “至少有一个能”的反面是“都不能”.
答案 a,b都不能被5整除
9.下列条件:①ab>0,②ab<0,③a>0,b>0,④a<0,b<0,其中能使+≥2成立的条件的序号是________.
解析 要使+≥2,只需>0成立,即a,b不为0且同号即可,故①③④能使+≥2成立.
答案 ①③④
12
10.给出如下四个命题:①e>2;②ln 2>;③π2<3π;④<,正确的命题是________(只填序号).
解析 要证e>2,只要证>ln 2,即2>eln 2,
设f(x)=eln x-x,x>0,∴f′(x)=-1=,
当0<x<e时,f′(x)>0,函数单调递增,
当x>e时,f′(x)<0,函数单调递减,
∴f(x)<f(e)=eln e-e=0,∴f(2)=eln 2-2<0,
即2>eln 2,∴e>2,因此①正确;
∵3ln 2=ln 8>ln 2.82>ln e2=2.
∴ln 2>,因此②正确;
π2<42=16,3π>33=27,因此π2<3π,③正确;
∵2π<π2,∴<,④正确;
正确的命题是①②③④.
答案 ①②③④
三、解答题
11.若a,b,c是不全相等的正数,求证:
lg+lg+lg>lg a+lg b+lg c.
证明 ∵a,b,c∈(0,+∞),
∴≥>0,≥>0,≥>0.
又上述三个不等式中等号不能同时成立.
∴··>abc成立.
上式两边同时取常用对数,
得lg>lg abc,
∴lg+lg+lg>lg a+lg b+lg c.
12.设数列{an}是公比为q的等比数列,Sn是它的前n项和.
(1)求证:数列{Sn}不是等比数列;
12
(2)数列{Sn}是等差数列吗?为什么?
(1)证明 假设数列{Sn}是等比数列,则S=S1S3,
即a(1+q)2=a1·a1·(1+q+q2),
因为a1≠0,所以(1+q)2=1+q+q2,
即q=0,这与公比q≠0矛盾,
所以数列{Sn}不是等比数列.
(2)解 当q=1时,Sn=na1,故{Sn}是等差数列;
当q≠1时,{Sn}不是等差数列,
否则2S2=S1+S3,即2a1(1+q)=a1+a1(1+q+q2),
得q=0,这与公比q≠0矛盾.
综上,当q=1时,数列{Sn}是等差数列;当q≠1时,数列{Sn}不是等差数列.
能力提升题组
13.已知函数f(x)=,a,b是正实数,A=f,B=f(),C=f,则A,B,C的大小关系为( )
A.A≤B≤C B.A≤C≤B
C.B≤C≤A D.C≤B≤A
解析 ∵≥≥,又f(x)=在R上是减函数,∴f≤f()≤f.
答案 A
14.设a,b,c均为正实数,则三个数a+,b+,c+( )
A.都大于2 B.都小于2
C.至少有一个不大于2 D.至少有一个不小于2
解析 ∵a>0,b>0,c>0,
∴++=++
≥6,当且仅当a=b=c=1时,“=”成立,故三者不能都小于2,即至少有一个不小于2.
答案 D
12
15.如果a+b>a+b,则a,b应满足的条件是________.
解析 ∵a+b-(a+b)
=(a-b)+(b-a)
=(-)(a-b)
=(-)2(+).
∴当a≥0,b≥0且a≠b时,(-)2(+)>0.
∴a+b>a+b成立的条件是a≥0,b≥0且a≠b.
答案 a≥0,b≥0且a≠b
16.设x≥1,y≥1,证明x+y+≤++xy.
证明 由于x≥1,y≥1,
所以要证明x+y+≤++xy,
只需证xy(x+y)+1≤y+x+(xy)2.
将上式中的右式减左式,得
[y+x+(xy)2]-[xy(x+y)+1]
=[(xy)2-1]-[xy(x+y)-(x+y)]
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1).
因为x≥1,y≥1,所以(xy-1)(x-1)(y-1)≥0,
从而所要证明的不等式成立.
17.(2016·浙江卷)设函数f(x)=x3+,x∈[0,1],证明:
(1)f(x)≥1-x+x2;
(2)<f(x)≤.
证明 (1)因为1-x+x2-x3==,
由于x∈[0,1],有≤,
即1-x+x2-x3≤,
所以f(x)≥1-x+x2.
12
(2)由0≤x≤1得x3≤x,故f(x)=x3+≤x+=x+-+=+≤,
所以f(x)≤.
由(1)得f(x)≥1-x+x2=+≥,
又因为f=>,
所以f(x)>.
综上,<f(x)≤.
12