- 2023-05-31 发布 |
- 37.5 KB |
- 28页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018年甘肃省张掖市中考数学试卷
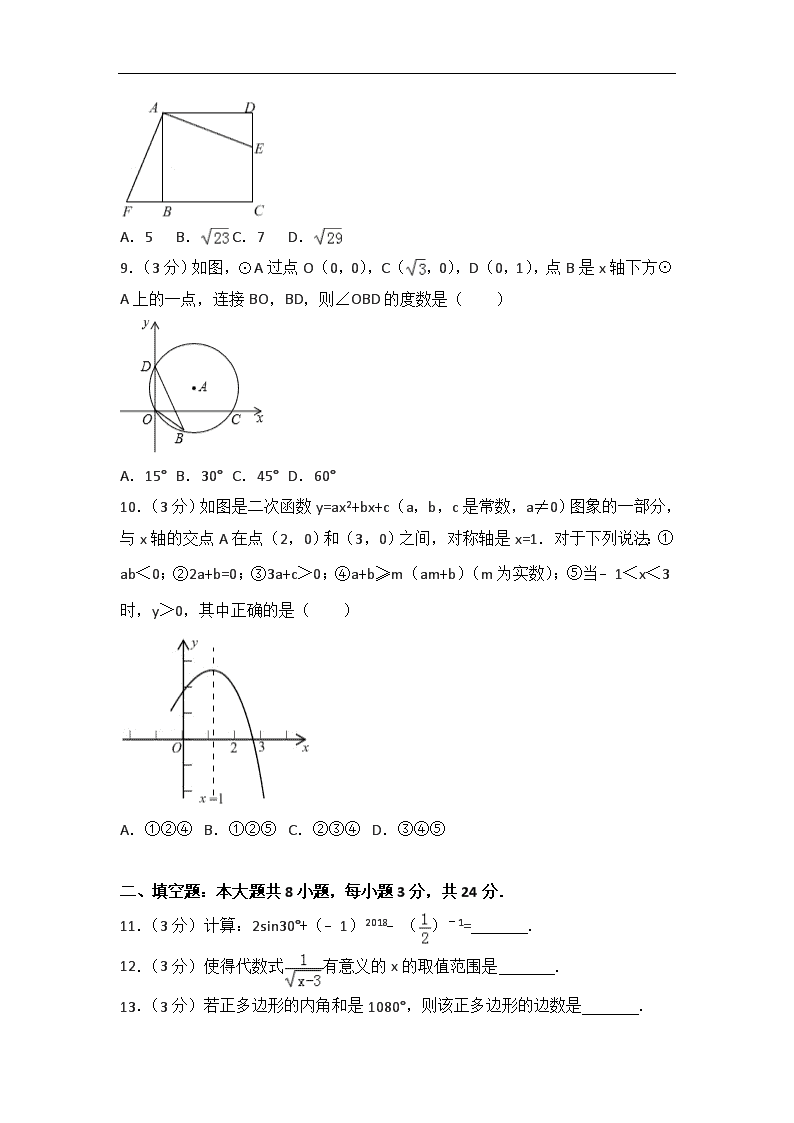
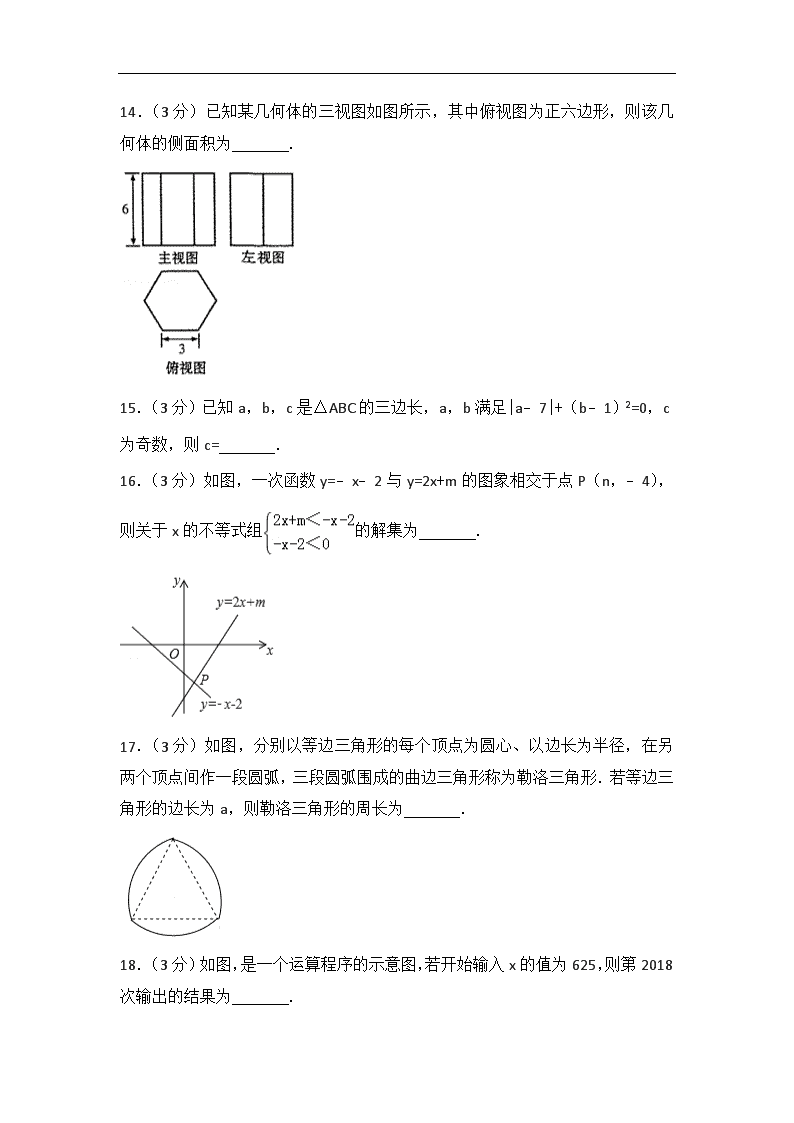
2018年甘肃省张掖市中考数学试卷 一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项. 1.(3分)﹣2018的相反数是( ) A.﹣2018 B.2018 C.﹣ D. 2.(3分)下列计算结果等于x3的是( ) A.x6÷x2 B.x4﹣x C.x+x2 D.x2•x 3.(3分)若一个角为65°,则它的补角的度数为( ) A.25° B.35° C.115° D.125° 4.(3分)已知=(a≠0,b≠0),下列变形错误的是( ) A.= B.2a=3b C.= D.3a=2b 5.(3分)若分式的值为0,则x的值是( ) A.2或﹣2 B.2 C.﹣2 D.0 6.(3分)甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数与方差s2如下表: 甲 乙 丙 丁 平均数(米) 11.1 11.1 10.9 10.9 方差s2 1.1 1.2 1.3 1.4 若要选一名成绩好且发挥稳定的同学参加比赛,则应该选择( ) A.甲 B.乙 C.丙 D.丁 7.(3分)关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( ) A.k≤﹣4 B.k<﹣4 C.k≤4 D.k<4 8.(3分)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为( ) A.5 B. C.7 D. 9.(3分)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( ) A.15° B.30° C.45° D.60° 10.(3分)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( ) A.①②④ B.①②⑤ C.②③④ D.③④⑤ 二、填空题:本大题共8小题,每小题3分,共24分. 11.(3分)计算:2sin30°+(﹣1)2018﹣()﹣1= . 12.(3分)使得代数式有意义的x的取值范围是 . 13.(3分)若正多边形的内角和是1080°,则该正多边形的边数是 . 14.(3分)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 . 15.(3分)已知a,b,c是△ABC的三边长,a,b满足|a﹣7|+(b﹣1)2=0,c为奇数,则c= . 16.(3分)如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组的解集为 . 17.(3分)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为 . 18.(3分)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2018次输出的结果为 . 三、解答题(一):本大题共5小题,满分26分,解答应写出必要的文字说明、证明过程或演算步骤. 19.(4分)计算:÷(﹣1) 20.(4分)如图,在△ABC中,∠ABC=90°. (1)作∠ACB的平分线交AB边于点O,再以点O为圆心,OB的长为半径作⊙O;(要求:不写做法,保留作图痕迹) (2)判断(1)中AC与⊙O的位置关系,直接写出结果. 21.(6分)《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题. 22.(6分)随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4) 23.(6分)如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案. (1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少? (2)现将方格内空白的小正方形(A,B,C,D,E,F)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率. 四、解答题(二):本大题共5小题,满分40分.解答应写出必要的文宇说明、证明过程或演算步骤. 24.(7分)“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分) 根据所给信息,解答以下问题: (1)在扇形统计图中,C对应的扇形的圆心角是 度; (2)补全条形统计图; (3)所抽取学生的足球运球测试成绩的中位数会落在 等级; (4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人? 25.(7分)如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C. (1)求此反比例函数的表达式; (2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标. 26.(8分)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点. (1)求证:△BGF≌△FHC; (2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积. 27.(8分)如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF. (1)求证:∠C=90°; (2)当BC=3,sinA=时,求AF的长. 28.(10分)如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点. (1)求二次函数y=ax2+2x+c的表达式; (2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标; (3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积. 2018年甘肃省张掖市中考数学试卷 参考答案与试题解析 一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项. 1.(3分)﹣2018的相反数是( ) A.﹣2018 B.2018 C.﹣ D. 【分析】直接利用相反数的定义分析得出答案. 【解答】解:﹣2018的相反数是:2018. 故选:B. 2.(3分)下列计算结果等于x3的是( ) A.x6÷x2 B.x4﹣x C.x+x2 D.x2•x 【分析】根据同底数幂的除法、乘法及同类项的定义逐一计算即可得. 【解答】解:A、x6÷x2=x4,不符合题意; B、x4﹣x不能再计算,不符合题意; C、x+x2不能再计算,不符合题意; D、x2•x=x3,符合题意; 故选:D. 3.(3分)若一个角为65°,则它的补角的度数为( ) A.25° B.35° C.115° D.125° 【分析】根据互为补角的两个角的和等于180°列式进行计算即可得解. 【解答】解:180°﹣65°=115°. 故它的补角的度数为115°. 故选:C. 4.(3分)已知=(a≠0,b≠0),下列变形错误的是( ) A.= B.2a=3b C.= D.3a=2b 【分析】根据两内项之积等于两外项之积对各选项分析判断即可得解. 【解答】解:由=得,3a=2b, A、由等式性质可得:3a=2b,正确; B、由等式性质可得2a=3b,错误; C、由等式性质可得:3a=2b,正确; D、由等式性质可得:3a=2b,正确; 故选:B. 5.(3分)若分式的值为0,则x的值是( ) A.2或﹣2 B.2 C.﹣2 D.0 【分析】直接利用分式的值为零则分子为零进而得出答案. 【解答】解:∵分式的值为0, ∴x2﹣4=0, 解得:x=2或﹣2. 故选:A. 6.(3分)甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数与方差s2如下表: 甲 乙 丙 丁 平均数(米) 11.1 11.1 10.9 10.9 方差s2 1.1 1.2 1.3 1.4 若要选一名成绩好且发挥稳定的同学参加比赛,则应该选择( ) A.甲 B.乙 C.丙 D.丁 【分析】根据平均数和方差的意义解答. 【解答】解:从平均数看,成绩好的同学有甲、乙, 从方差看甲、乙两人中,甲方差小,即甲发挥稳定, 故选:A. 7.(3分)关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( ) A.k≤﹣4 B.k<﹣4 C.k≤4 D.k<4 【分析】根据判别式的意义得△=42﹣4k≥0,然后解不等式即可. 【解答】解:根据题意得△=42﹣4k≥0, 解得k≤4. 故选:C. 8.(3分)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为( ) A.5 B. C.7 D. 【分析】利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积,进而可求出正方形的边长,再利用勾股定理得出答案. 【解答】解:∵把△ADE顺时针旋转△ABF的位置, ∴四边形AECF的面积等于正方形ABCD的面积等于25, ∴AD=DC=5, ∵DE=2, ∴Rt△ADE中,AE==. 故选:D. 9.(3分)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( ) A.15° B.30° C.45° D.60° 【分析】连接DC,利用三角函数得出∠DCO=30°,进而利用圆周角定理得出∠DBO=30°即可. 【解答】解:连接DC, ∵C(,0),D(0,1), ∴∠DOC=90°,OD=1,OC=, ∴∠DCO=30°, ∴∠OBD=30°, 故选:B. 10.(3分)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( ) A.①②④ B.①②⑤ C.②③④ D.③④⑤ 【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b=0;当x=﹣1时,y=a﹣b+c;然后由图象确定当x取何值时,y>0. 【解答】解:①∵对称轴在y轴右侧, ∴a、b异号, ∴ab<0,故正确; ②∵对称轴x=﹣=1, ∴2a+b=0;故正确; ③∵2a+b=0, ∴b=﹣2a, ∵当x=﹣1时,y=a﹣b+c<0, ∴a﹣(﹣2a)+c=3a+c<0,故错误; ④根据图示知,当m=1时,有最大值; 当m≠1时,有am2+bm+c≤a+b+c, 所以a+b≥m(am+b)(m为实数). 故正确. ⑤如图,当﹣1<x<3时,y不只是大于0. 故错误. 故选:A. 二、填空题:本大题共8小题,每小题3分,共24分. 11.(3分)计算:2sin30°+(﹣1)2018﹣()﹣1= 0 . 【分析】根据特殊角的三角函数值、幂的乘方和负整数指数幂可以解答本题. 【解答】解:2sin30°+(﹣1)2018﹣()﹣1 =2×+1﹣2 =1+1﹣2 =0, 故答案为:0. 12.(3分)使得代数式有意义的x的取值范围是 x>3 . 【分析】二次根式中被开方数的取值范围:二次根式中的被开方数是非负数. 【解答】解:∵代数式有意义, ∴x﹣3>0, ∴x>3, ∴x的取值范围是x>3, 故答案为:x>3. 13.(3分)若正多边形的内角和是1080°,则该正多边形的边数是 8 . 【分析】n边形的内角和是(n﹣2)•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数. 【解答】解:根据n边形的内角和公式,得 (n﹣2)•180=1080, 解得n=8. ∴这个多边形的边数是8. 故答案为:8. 14.(3分)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 108 . 【分析】观察该几何体的三视图发现该几何体为正六棱柱,然后根据提供的尺寸求得其侧面积即可. 【解答】解:观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6, 所以其侧面积为3×6×6=108, 故答案为:108. 15.(3分)已知a,b,c是△ABC的三边长,a,b满足|a﹣7|+(b﹣1)2=0,c为奇数,则c= 7 . 【分析】 根据非负数的性质列式求出a、b的值,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求出c的取值范围,再根据c是奇数求出c的值. 【解答】解:∵a,b满足|a﹣7|+(b﹣1)2=0, ∴a﹣7=0,b﹣1=0, 解得a=7,b=1, ∵7﹣1=6,7+1=8, ∴6<c<8, 又∵c为奇数, ∴c=7, 故答案是:7. 16.(3分)如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组的解集为 ﹣2<x<2 . 【分析】先将点P(n,﹣4)代入y=﹣x﹣2,求出n的值,再找出直线y=2x+m落在y=﹣x﹣2的下方且都在x轴下方的部分对应的自变量的取值范围即可. 【解答】解:∵一次函数y=﹣x﹣2的图象过点P(n,﹣4), ∴﹣4=﹣n﹣2,解得n=2, ∴P(2,﹣4), 又∵y=﹣x﹣2与x轴的交点是(﹣2,0), ∴关于x的不等式2x+m<﹣x﹣2<0的解集为﹣2<x<2. 故答案为﹣2<x<2. 17.(3分)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为 πa . 【分析】首先根据等边三角形的性质得出∠A=∠B=∠C=60°,AB=BC=CA=a,再利用弧长公式求出的长=的长=的长==,那么勒洛三角形的周长为×3=πa. 【解答】解:如图.∵△ABC是等边三角形, ∴∠A=∠B=∠C=60°,AB=BC=CA=a, ∴的长=的长=的长==, ∴勒洛三角形的周长为×3=πa. 故答案为πa. 18.(3分)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2018次输出的结果为 1 . 【分析】依次求出每次输出的结果,根据结果得出规律,即可得出答案. 【解答】解:当x=625时,x=125, 当x=125时,x=25, 当x=25时,x=5, 当x=5时,x=1, 当x=1时,x+4=5, 当x=5时,x=1, 当x=1时,x+4=5, 当x=5时,x=1, … (2018﹣3)÷2=1007.5, 即输出的结果是1, 故答案为:1 三、解答题(一):本大题共5小题,满分26分,解答应写出必要的文字说明、证明过程或演算步骤. 19.(4分)计算:÷(﹣1) 【分析】先计算括号内分式的减法,再计算除法即可得. 【解答】解:原式=÷(﹣) =÷ =• =. 20.(4分)如图,在△ABC中,∠ABC=90°. (1)作∠ACB的平分线交AB边于点O,再以点O为圆心,OB的长为半径作⊙ O;(要求:不写做法,保留作图痕迹) (2)判断(1)中AC与⊙O的位置关系,直接写出结果. 【分析】(1)首先利用角平分线的作法得出CO,进而以点O为圆心,OB为半径作⊙O即可; (2)利用角平分线的性质以及直线与圆的位置关系进而求出即可. 【解答】解:(1)如图所示: ; (2)相切;过O点作OD⊥AC于D点, ∵CO平分∠ACB, ∴OB=OD,即d=r, ∴⊙O与直线AC相切, 21.(6分)《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题. 【分析】设合伙买鸡者有x人,鸡的价格为y文钱,根据“如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱”,即可得出关于x、y的二元一次方程组,解之即可得出结论. 【解答】解:设合伙买鸡者有x人,鸡的价格为y文钱, 根据题意得:, 解得:. 答:合伙买鸡者有9人,鸡的价格为70文钱. 22.(6分)随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4) 【分析】过点C作CD⊥AB于点D,利用锐角三角函数的定义求出CD及AD的长,进而可得出结论. 【解答】解:过点C作CD⊥AB于点D, 在Rt△ADC和Rt△BCD中, ∵∠CAB=30°,∠CBA=45°,AC=640, ∴CD=320,AD=320, ∴BD=CD=320,BC=320, ∴AC+BC=640+320≈1088, ∴AB=AD+BD=320+320≈864, ∴1088﹣864=224(公里), 答:隧道打通后与打通前相比,从A地到B地的路程将约缩短224公里. 23.(6分)如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案. (1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少? (2)现将方格内空白的小正方形(A,B,C,D,E,F)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率. 【分析】(1)直接利用概率公式计算可得; (2)列表得出所有等可能结果,从中找到新图案是轴对称图形的结果数,利用概率公式计算可得. 【解答】解:(1)∵正方形网格被等分成9等份,其中阴影部分面积占其中的3份, ∴米粒落在阴影部分的概率是=; (2)列表如下: A B C D E F A (B,A) (C,A) (D,A) (E,A) (F,A) B (A,B) (C,B) (D,B) (E,B) (F,B) C (A,C) (B,C) (D,C) (E,C) (F,C) D (A,D) (B,D) (C,D) (E,D) (F,D) E (A,E) (B,E) (C,E) (D,E) (F,E) F (A,F) (B,F) (C,F) (D,F) (E,F) 由表可知,共有30种等可能结果,其中是轴对称图形的有10种, 故新图案是轴对称图形的概率为=. 四、解答题(二):本大题共5小题,满分40分.解答应写出必要的文宇说明、证明过程或演算步骤. 24.(7分)“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分) 根据所给信息,解答以下问题: (1)在扇形统计图中,C对应的扇形的圆心角是 117 度; (2)补全条形统计图; (3)所抽取学生的足球运球测试成绩的中位数会落在 B 等级; (4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人? 【分析】(1)先根据B等级人数及其百分比求得总人数,总人数减去其他等级人数求得C等级人数,继而用360°乘以C等级人数所占比例即可得; (2)根据以上所求结果即可补全图形; (3)根据中位数的定义求解可得; (4)总人数乘以样本中A等级人数所占比例可得. 【解答】解:(1)∵总人数为18÷45%=40人, ∴C等级人数为40﹣(4+18+5)=13人, 则C对应的扇形的圆心角是360°×=117°, 故答案为:117; (2)补全条形图如下: (3)因为共有40个数据,其中位数是第20、21个数据的平均数,而第20、21个数据均落在B等级, 所以所抽取学生的足球运球测试成绩的中位数会落在B等级, 故答案为:B. (4)估计足球运球测试成绩达到A级的学生有300×=30人. 25.(7分)如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C. (1)求此反比例函数的表达式; (2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标. 【分析】(1)利用点A在y=﹣x+4上求a,进而代入反比例函数y=求k. (2)联立方程求出交点,设出点P坐标表示三角形面积,求出P点坐标. 【解答】解:(1)把点A(﹣1,a)代入y=x+4,得a=3, ∴A(﹣1,3) 把A(﹣1,3)代入反比例函数y= ∴k=﹣3, ∴反比例函数的表达式为y=﹣ (2)联立两个函数的表达式得 解得 或 ∴点B的坐标为B(﹣3,1) 当y=x+4=0时,得x=﹣4 ∴点C(﹣4,0) 设点P的坐标为(x,0) ∵S△ACP=S△BOC ∴ 解得x1=﹣6,x2=﹣2 ∴点P(﹣6,0)或(﹣2,0) 26.(8分)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点. (1)求证:△BGF≌△FHC; (2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积. 【分析】(1)根据三角形中位线定理和全等三角形的判定证明即可; (2)利用正方形的性质和矩形的面积公式解答即可. 【解答】解:(1)∵点F,G,H分别是BC,BE,CE的中点, ∴FH∥BE,FH=BE,FH=BG, ∴∠CFH=∠CBG, ∵BF=CF, ∴△BGF≌△FHC, (2)当四边形EGFH是正方形时,可得:EF⊥GH且EF=GH, ∵在△BEC中,点,H分别是BE,CE的中点, ∴GH=,且GH∥BC, ∴EF⊥BC, ∵AD∥BC,AB⊥BC, ∴AB=EF=GH=a, ∴矩形ABCD的面积=. 27.(8分)如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF. (1)求证:∠C=90°; (2)当BC=3,sinA=时,求AF的长. 【分析】(1)连接OE,BE,因为DE=EF,所以,从而易证∠OEB=∠DBE,所以OE∥BC,从可证明BC⊥AC; (2)设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sinA===,从而可求出r的值. 【解答】解:(1)连接OE,BE, ∵DE=EF, ∴ ∴∠OBE=∠DBE ∵OE=OB, ∴∠OEB=∠OBE ∴∠OEB=∠DBE, ∴OE∥BC ∵⊙O与边AC相切于点E, ∴OE⊥AC ∴BC⊥AC ∴∠C=90° (2)在△ABC,∠C=90°,BC=3,sinA= ∴AB=5, 设⊙O的半径为r,则AO=5﹣r, 在Rt△AOE中,sinA=== ∴r= ∴AF=5﹣2×= 28.(10分)如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点. (1)求二次函数y=ax2+2x+c的表达式; (2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标; (3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积. 【分析】(1)根据待定系数法,可得函数解析式; (2)根据菱形的对角线互相垂直且平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得P点坐标; (3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PQ的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案. 【解答】解:(1)将点B和点C的坐标代入函数解析式,得 , 解得, 二次函数的解析是为y=﹣x2+2x+3; (2)若四边形POP′C为菱形,则点P在线段CO的垂直平分线上, 如图1,连接PP′,则PE⊥CO,垂足为E, ∵C(0,3), ∴E(0,), ∴点P的纵坐标, 当y=时,即﹣x2+2x+3=, 解得x1=,x2=(不合题意,舍), ∴点P的坐标为(,); (3)如图2, P在抛物线上,设P(m,﹣m2+2m+3), 设直线BC的解析式为y=kx+b, 将点B和点C的坐标代入函数解析式,得 , 解得. 直线BC的解析为y=﹣x+3, 设点Q的坐标为(m,﹣m+3), PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m. 当y=0时,﹣x2+2x+3=0, 解得x1=﹣1,x2=3, OA=1, AB=3﹣(﹣1)=4, S四边形ABPC=S△ABC+S△PCQ+S△PBQ =AB•OC+PQ•OF+PQ•FB =×4×3+(﹣m2+3m)×3 =﹣(m﹣)2+, 当m=时,四边形ABPC的面积最大. 当m=时,﹣m2+2m+3=,即P点的坐标为(,). 当点P的坐标为(,)时,四边形ACPB的最大面积值为. 查看更多