- 2021-02-26 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海教育高中数学一下同角三角比的关系和诱导公式篇
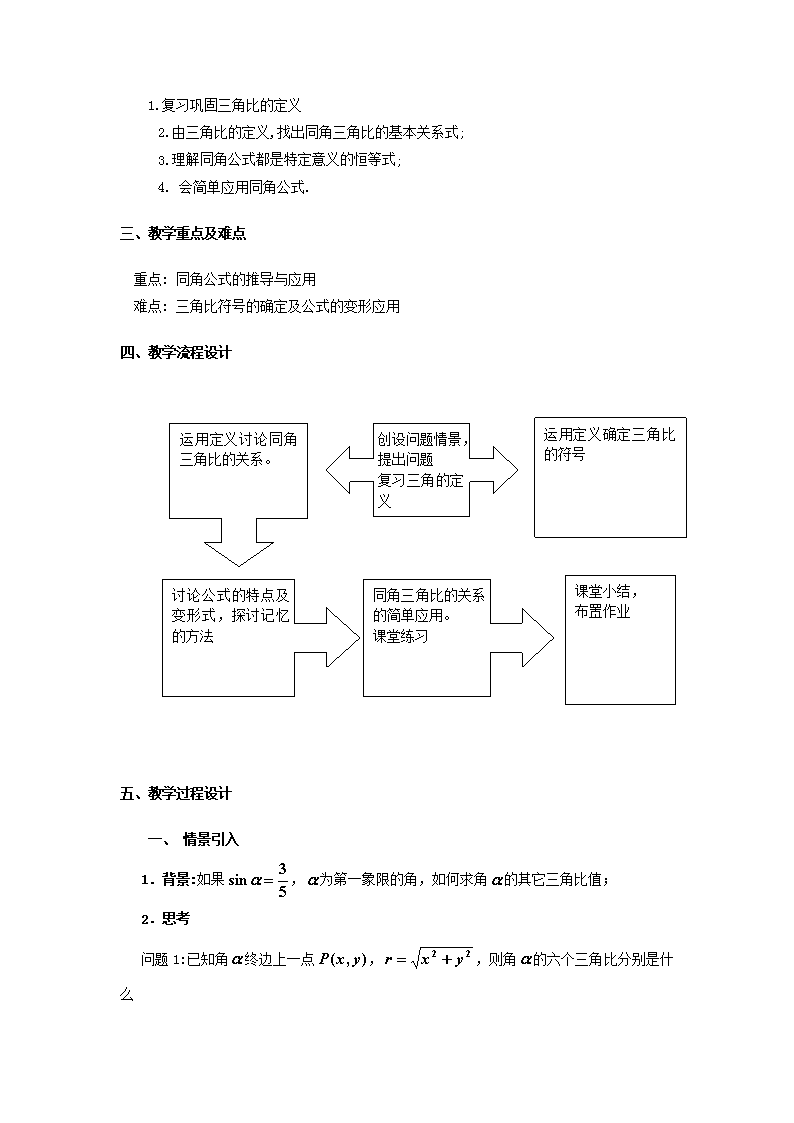
5.3(1)同角三角比的关系与诱导公式 上海市杨浦高级中学 江海涛 一、教学内容分析 当我们把角的概念推广到任意角以后,给出了任意角的三角比的定义,为了求任意角的三角比的值,由三角比的定义探求同角三角比的关系和诱导公式,成为本节我们要研究的课题。 同角三角比间的八个关系式,主要用于: (1)已知某角的一个三角比的值,求它的其余各三角比的值; (2)化简三角比的关系式; (3)证明三角恒等式 (4)解三角方程。 鉴于八个关系式的应用如此之广,因此要牢固掌握,并能灵活运用。记一个公式时,还要灵活地写出这个公式的某些变形,熟记这些公式对以后的学习是必要的。 诱导公式沟通了任意角三角比与锐角三角比以及终边有特殊位置关系的角的三角比之间的联系.在求任意角的三角比的值,解决有关的三角变换等方面有重要的作用。 由角的终边的某种对称性,导致终边与单位圆的交点也具有相应的对称性,这样就产生了“”、“”、“”等诱导公式,我们知道,角的终边与角的终边关于y轴对称;角的终边与角的终边关于原点对称,,角的终边与角的终边关于x轴对称,所以、、、各角的三角函数值与角的三角比的绝对值相同,符号由各角所在象限的原三角比的符号来确定,诱导公式有很多,但是抓住终边的对称性及三角比定义,明白公式的来龙去脉也就不难记忆了。 诱导公式可以帮助我们把任意角的三角比化为锐角三角比,在求任意角的三角比时起很大作用,但是随着计算器的普及,诱导公式更多地运用在三角变换中,特别是诱导公式中的角可以是任意角,即,它在终边具有某种对称性的角的三角比变换中,应用广泛,如后续课中,画余弦曲线就是利用诱导公式把正弦曲线向左平移个长度单位而得到的。 在教学中,提供给学生的记忆方法一定要重在理解、重在思考,以达到优化思维品质的功效.用一句话归纳概括诱导公式一、二、三、四、五并能正确理解这句话中每一词语的含义,是本节教材的难点.讲清每一组公式的意义及其中符号语言的特征,并把公式与相应图形对应起来,是突破这个难点的关键。 二、教学目标设计 1.复习巩固三角比的定义m] 2.由三角比的定义,找出同角三角比的基本关系式; 3.理解同角公式都是特定意义的恒等式; 4. 会简单应用同角公式. 三、教学重点及难点 重点: 同角公式的推导与应用 难点: 三角比符号的确定及公式的变形应用 四、教学流程设计 讨论公式的特点及变形式,探讨记忆的方法 创设问题情景,提出问题 复习三角的定义 运用定义确定三角比的符号 运用定义讨论同角三角比的关系。 课堂小结, 布置作业 同角三角比的关系的简单应用。 课堂练习 五、教学过程设计 一、 情景引入 1.背景:如果,为第一象限的角,如何求角的其它三角比值; 2.思考 问题1:已知角终边上一点,,则角的六个三角比分别是什么 问题2:当角分别在不同的象限时,的符号分别是怎样的? 3.讨论:由于的三角比都是由表示的,则角的六个三角比之间有什么关系? 二、学习新课 1.探求公式 (板书课题:同角的三角比的基本关系) 1.由三角比的定义,我们可以得到以下关系: 理论证明:(采用定义) (1)倒数关系: (2)商数关系: (3)平方关系: [说明] ①注意“同角”,至于角的形式无关重要,如,等; ②注意这些关系式都是对于使它们有意义的角而言的,如; ③对这些关系式不仅要牢固掌握,还要能灵活运用(正用、反用、变形用),如 ,, 等 ④据此,由一个角的任一三角函数值可求出这个角的另两个三角函数值,且因为利用“平方关系”公式,最终需求平方根,会出现两解,因此应尽可能少用(实际上,至多只要用一次)。 2.例题分析 3.例题1:已知且为第四象限的角,求的其他三角比的值; 解:为第四象限的角, 提问:(1)如果去掉为第四象限的角这个条件,应如何求的其他三角比的值? (2)练习:已知,求的其他三角比的值? 4.例题2:已知 ,求和; 解: ∵,∴ ∵,∴是第一或第三象限角 当是第一象限角时, 当是第三象限角时, 提问:你能用学过锐角三角比来解答上述问题吗? (1)利用直角三角形计算三角比的值; (2)利用象限角确定三角比的符号. [说明]已知一个角的某一个三角比的值,便可运用基本关系式求出其它三角比的值。在求值中,确定角的终边位置是关键和必要的。有时,由于角的终边位置的不确定,因此解的情况不止一种。解题时产生遗漏的主要原因是:①没有确定好或不去确定角的终边位置;②利用平方关系开平方时,漏掉了负的平方根。 5.例题3:已知 ,求; 解:[来 ∵,∴角的终边不在坐标轴上. 当是第一象限或第二象限角时 ,[ 当是第三象限或第四象限角时 , [说明](1)如果已知角的一个三角比和它所在的象限,那么角的其他三角比就可以唯一确定. 如果仅知道的一个三角比,那么就应该根据角的终边的所有可能的情况分别求出其他三角比. (2)例1是给出一个三角比的值,并给出了角所在的象限,这样的题目只有一组解;例2是给出一个三角比的值,未给出角所在的象限,要先确定角所在的象限,然后分情况求解,这样的题有两组解;例3是给出了一个三角比的值,但是字母,因此先要根据字母的取值确定所在的位置. 3.归纳总结: 总结解题的一般步骤: ①确定终边的位置(判断所求三角函数的符号); ②根据同角三角函数的关系式求值 三、巩固练习 练习5.3(1) 四、课堂小结 1.同角三角函数基本关系式及成立的条件; 2.根据一个角的某一个三角函数值求其它三角函数值; 3.在以上的题型中:先确定角的终边位置,再根据关系式求值。 五、作业布置 习题5.3A组:2,4(3)(4),7;B组:2, 七、教学设计说明 本节课主要以下几个层次教学: 第一层次:复习三角比的定义,为学习同角公式打下基础; 第二层次:运用三角比的定义,探求同角公式 第三层次:这八个公式的特点是同一个角不同的三角比之间的关系,因此要注意公式的特点。在记忆公式中,还要注意它们变形形式的应用;此外,在公式的记忆上,根据学生的情况,可教给学生“正六边形”记忆法。 第四个层次,同角公式的简单应用。 这几个例题主要是练习公式的应用,注意什么情况下是一组解,什么情况下是两组解,什么情况下是四组解(即两种形式)。 5.3(2)同角三角比的关系与诱导公式 上海市杨浦高级中学 江海涛 一、教学目标设计 1.掌握诱导公式的推导方法和记忆方法; 2.会运用这些公式求解任意角的三角比的值,会由三角比的值,求特殊角,并会化简单的三角比的关系式; 3.通过公式的探求与应用培养思维的严密性. 三、教学重点及难点 重点:诱导公式 难点:诱导公式的灵活应用 四、教学流程设计 复习公式一引入 运用化归思想由公式三导出公式 四 根据三角比的定义 和单位圆公式二、三 例题分析,运用诱导公式求值、化简及给值求角 课堂练习 课堂小结, 布置作业 五、教学过程设计 一、 复习引入 1.公式一: (其中) 用角度可写成:[ (其中) 2 .讨论 公式一的作用:把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切,其方法是先在0º―360º内找出与角终边相同的角,再把它写成诱导公式一的形式,然后得出结果. 这组公式可以统一概括为的形式,上述一组公式叫做任意角三角比的第一组诱导公式,其特征是:等号两边是同名三角比,且符号都为正. a a - x y P(x,y) P’(x,-y) O M 说明]运用公式时,注意“弧度”与“角度”两种度量制不要混用,如写成,是不对的. 二、学习新课 1.公式推导 公式二: 它说明角-与角的正弦值互为相反数,而它们的余弦值相等.这是因为,若角的终边与单位圆交于点P(x,y),则角-的终边与单位圆的交点必为P´(x,-y)(如图1).由正弦、余弦三角比的定义,即可得 sin=y, cos=x, sin(-)=-y, cos(-)=x 所以:sin(-)= -sin, cos(-)= cosα 由三角比的商数关系,得: 即 类似可得 这组公式叫任意角三角比的第二组诱导公式 练习:求的正弦、余弦、正切和余切的值. [说明]公式二也可以由特殊到一般,既从特殊三角比的计算,猜测出公式,再证明. 公式三: M P(x,y) y M’ a + o 180 a x P’(-x,-y) O 用角度可表示如下: [ m] 它刻画了角180º+与角的正弦值(或余弦值)之间的关系,这个关系是:以角终边的反向延长线为终边的角的正弦值(或余弦值)与角的正弦值(或余弦值)是一对相反数.这是因为若设的终边与单位圆交于点P( x,y),则角终边的反向延长线,即180º+角的终边与单位圆的交点必为P´(-x,-y)(如图2).由正弦、余弦三角比的定义,即可得sin=y, cos=x, sin(180º+)=-y, cos(180º+)=-x, 所以 :sin(180º+)=-sin,cos(180º+)=-cos. [说明]公式二、三的获得主要借助于单位圆及正弦、余弦比的定义.根据点P的坐标准确地确定点P´的坐标是关键,这里充分利用了对称的性质.直观的对称形象为我们准确写出P´的坐标铺平了道路,体现了数形结合这一数学思想的优越性. 练习:求下列三角比的值: (1); (2)[ 分析:本题是诱导公式二的巩固性练习题.求解时,只须设法将所给角分解成180º+或(π+),为锐角即可. 解:(1)cos210º=cos(180º+30º)=-cos30º=- (2)sin=sin()=-sin=-. 公式四: 把第三组公式中的换成,得第四组诱导公式: [说明]这组公式均可由前面学过的诱导公式直接推出,体现了把未知问题化为已知问题处理这一化归的数学思想.公式的推导并不难,然而推导中的化归意识和策略是值得我们关注的. 四组诱导公式可概括为: k·360º+(k∈Z),-,180º±,360º-的三角比值,等于的同名三角比的值,前面加上一个把看成锐角时原三角比的符号. [说明]这里的“同名三角比值”是指等号两边的三角比名称相同;“把看成锐角”是指原本是任意角,这里只是把它视为锐角处理;“前面加上一个……符号”是指的同名三角比值未必就是最后结果,前面还应添上一个符号(正号或负号,主要是负号,正号可省略),而这个符号是把任意角视为锐角情况下的原三角比的符号.应注意讲清这句话中每一词语的含义,特别要讲清为什么要把任意角α看成锐角.建议通过实例分析说明. 练习:求下列各式的值:(1)sin(-);(2)cos(-60º)-sin(-210º) 分析:本题是诱导公式二、三的巩固性练习题.求解时一般先用诱导公式三把负角的正弦、余弦化为正角的正弦、余弦,然后再用诱导公式二把它们化为锐角的正弦、余弦来求. 解:(1)sin(-)=-sin()=sin=; (2)原式=cos60º+sin(180º+30º)=cos60º-sin30º=-=0 2.例题分析 例1:利用诱导公式,求下列各三角比: (1); (2) 例2化简: 例3根据条件,求角: (1) 已知; (2)已知. [说明]由三角比求特殊角的问题,是个“反”问题,对学生是个难点问题,教师可先缩小范围,如考虑在[0,]上,求角,再考虑等. 三、巩固练习[ P49 练习 5.3(2) 四、课堂小结 通过本节课的教学,我们获得了诱导公式.值得注意的是公式右端符号的确定.在运用诱导公式进行三角比的求值或化简中,我们又一次使用了转化的数学思想.通过进行角的适当配凑,使之符合诱导公式中角的结构特征,培养了我们思维的灵活性. 五、作业布置 习题5.3 A组:1;4(1)(2);5 B组:1;4查看更多