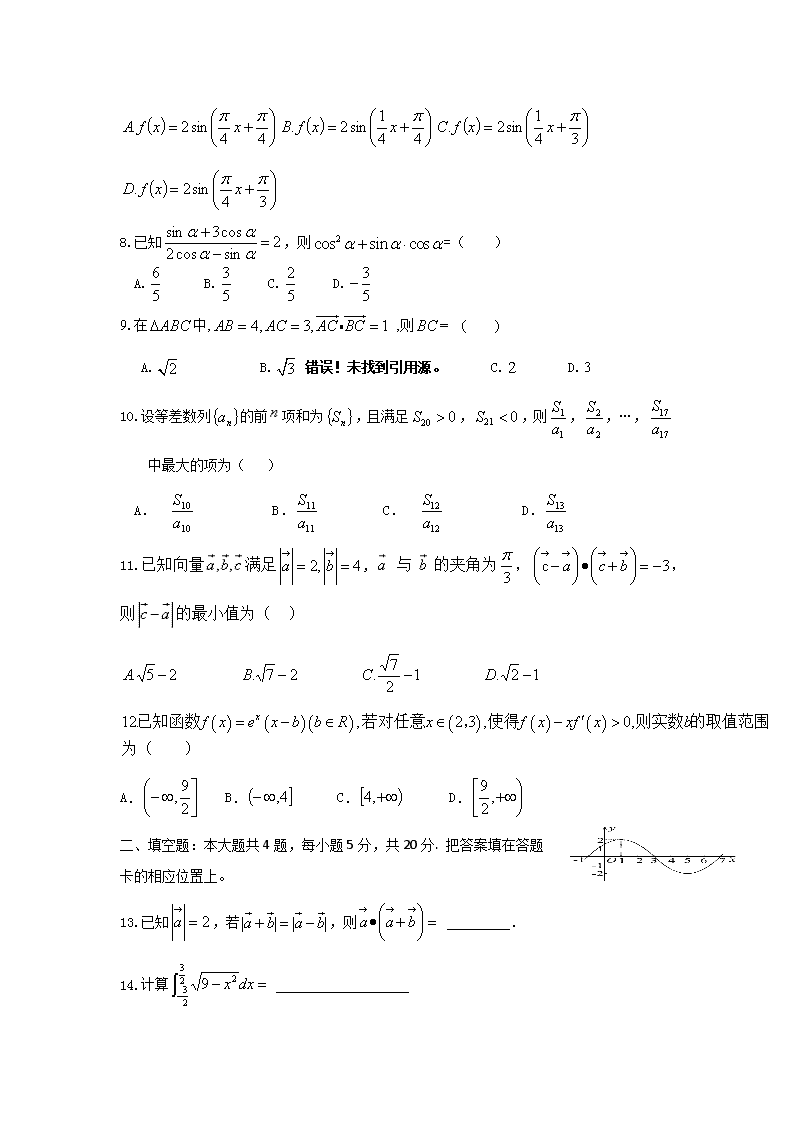数学(理)卷·2018届福建省福州市八县一中高三上学期期中考试(2017
2017---2018 学年度第一学期八县(市)一中期中联考
高中 三 年 数学(理科) 科试卷
考试日期:11 月 16 日 完卷时间:120 分钟 满 分:150 分
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分. 在每小题给出的四个选项中,只有
一项是符合题意要求的.
( )
A. B. C. D.
2.已知 ,其中 是虚数单位,则 的虚部为( )
A. B. C. D.
3.已知命题 :若 ,则 .命题 : .则下列命题为真命题的是
( )
A. B. C. D.
4.已知数列 为等比数列,且 ,则 的值为 ( )
A. B. C. 错误!未找到引用源。 D.
5.设 则( )
A. B. C. D.
6.已知 中,内角 所对边的长分别为 ,若 ,则
的面积等于( )
A. B. C. D.
7.已知函数 的图象的一部分如图所示,则函数
的解析式是( )
{ } ( )21. , 3 3 , 01
x
U
xU R A x B x A C Bx
− = = > = > ∩ = + 设 ,则
{ |1 2}x x≤ < { |-1< 2}x x ≤ { | 2}x x ≥ { | 2}x x >
1 21 3 , 3z i z i= + = + i 1
2
z
z
1− 4
5 i− 4
5 i
p *x N∈ x Z∈ q 11,( ) 02
xx R −∃ ∈ =
p¬ p q∧ p q¬ ∨ ( ) ( )p q¬ ¬∨
{ }na π42 2
7113 =+ aaa ( )122tan aa
3± 3− 3 3
3
−
1
2018
2017 2018
12017 , log 2018, log 2017a b c= = =
c b a> > b c a> > a c b> > a b c> >
ABC∆ , ,A B C , ,a b c , 2 cos , 23A b a B c
π= = =
ABC∆
3
8
3
4
3
2 3
( ) sin( )( 0,| | , )2f x A x A x R
πω ϕ ϕ= + > < ∈
( )f x
8.已知 ,则 =( )
A. B. C. D.
9.在 中, ,则 = ( )
A. B. 错误!未找到引用源。 C. D.
10.设等差数列 的前 项和为 ,且满足 , ,则 , ,…,
中最大的项为( )[]
A. B. C. D. []
11.已知向量 满足 , 与 的夹角为 , ,
则 的最小值为( ) []
A. B. C. D.
二、填空题:本大题共 4 题,每小题 5 分,共 20 分. 把答案填在答题
卡的相应位置上。
13.已知 ,若 ,则 .
14.计算
( )
+=
44sin2.
ππ
xxfA ( )
+=
44
1sin2.
π
xxfB ( )
+=
34
1sin2.
π
xxfC
( )
+=
34sin2.
ππ
xxfD
2sincos2
cos3sin =−
+
αα
αα 2cos sin cosα α α+ ⋅
6
5
3
5
2
5
3
5
−
ABC∆ 4, 3, 1AB AC AC BC= = =
BC
2 3 2 3
{ }na { }nS 020 >S 021
已知函数 若对任意 , 使得 则实数 的取值范围
为( )
∞−
2
9, ( ]4,∞− [ )+∞4,
+∞,2
9
2=
→
a | | | |a b a b+ = − =
+•
→→→
baa
=−∫−
dxx2
3
2
3
29
15.等差数列 中, 为其前 项和,若 , ,则 =
.
16.已知函数 ,则关于 的不等式
的解集为
三、解答题:本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分 10 分)
设 :实数 满足: ; :实数 满足:
.
(Ⅰ)若 ,且 为真,求实数 的取值范围;
(Ⅱ) 是 的必要不充分条件,求实数 的取值范围.
18.(本小题满分 12 分)
已知函数 图像关于 轴对称,
且相邻两对称轴间的距离为 .
(Ⅰ)求 的单调递增区间;[来 Com]
(Ⅱ)将函数 的图象沿 轴方向向右平移 个单位长度,再把横坐标缩短到原来的
(纵坐标不变),得到函数 的图象.当 时,求函数 的值域.
{ }na nS n 5 10a = 5 30S =
1 2 3 2017
1 1 1 1
S S S S
+ + + +
2
2017( ) 2017 log ( 1 ) 2017 3x xf x x x−= + + − − + x
( ) ( ) 6662 >++− xfxxf
p t 2 25 4 0( 0)t at a a− + < > q t
3 53 , (1,2)2t x x x= − + ∈
1
4a = p q∧ t
q p a
2( ) 3sin( ) 2sin 1( 0,0 )2
xf x x
ω ϕω ϕ ω ϕ π+= + + − > < < y
2
π
( )f x
( )y f x= x 6
π
1
2 ( )y g x= [ , ]12 6x
π π∈ − ( )g x
19.(本小题满分 12 分)
已知函数 .
(Ⅰ)若函数 的切线方程为 ,求实数 的值;
(Ⅱ)是否存在实数 使得关于的 方程 在 上恰有两个不等的
实根,若存在求 的取值范围,若不存在请说明理由.
20.(本小题满分 12 分)
21.(本小题满分 12 分)
21( ) ln 4f x x x= −
( )xf mxy +−=
2
1 m
b x bxxxf ++−=
2
3
2
1)( 2 [ ]4,1
b
{ } ( )∗
+ ∈+== Nnaaaa nnn 43,1 11中,数列
( ) { }通项公式;求数列 na1
( ) { } .4
3
3
1,,22 <≤+= nnn
n
n SSnba
nb 证明项和为前数列设
在 中,角 所对的边分别为 ,满足
(I)求角 ;
(Ⅱ)设 是边 上一点,若 求 的面积.
22.(本小题满分 12 分)
已知函数 ,其中 , .
2017---2018 学年度第
一学期八县(市)一中期中联考
高中 三 年 数学(理科) 科试卷答案
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分. 在每小题给出的四个选项中,只有
一项是符合题意要求的。
1-5 CBDCD 6-10 DAADA 11-12 BD[]
二、填空题:本大题共 4 题,每小题 5 分,共 20 分. 把答案填在答题卡的相应位置上。
13. 4 14. 15. 16.
三、解答题:本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分 10 分)
解: ,得 ;
:实数 满足:
ABC∆ , ,A B C , ,a b c ( ) 1cos32cos =+− CAB
B
D AB 2,CD = ,4,62 == ADb BCD
( ) ( ) ( )xhxgxf •= ( ) 21
1
x
axxg +
−= ( ) xexh =
( )g x( 1) 求 的单调区间;
( ) ( )( )1 2 1 2 1 21, 0.a f x f x x x x x= = ≠ + <( 2) 若 且 时,证明:
34
9
2
3 +π
2018
2017 ( )32,
( )0045 22 ><+− aaatt
( ) ( )( ) ( ) ( )2,1,2
53,0,2,1;11333,2,1,2
53 323 ∈+−=>′∈−+=−=′∈+−= xxxttxxxxtxxxt
是增函数, ………………………………………………………3
(Ⅰ) 时, : ; : ∵ 为真∴ 真且 真
∴ ,得 ,即实数 的取值范围为
…………………………………………6
(II) 是 的必要不充分条件,记 ,则 A 是 B 的真子集
∴ 得 , 实数的取值范围是
…………………………………..…10
18.(本小题满分 12 分)
(Ⅰ)由题意得: ,
因为相邻两对称轴间的距离为 ,所以
又 因 为 函 数 关 于 轴 对 称 , 故 是 偶 函 数 , 所 以
,
且 , 所 以 , 故 函 数
————————4 分
要 使 单 调 递 增 , 需 满 足
所 以 函 数 的 增 区 间 为 .
————————8 分
( Ⅱ ) 由 题 意 可 得 :
, 即 函 数 的 值 域 为
————————12 分
19. (本小题满分 12 分)
(Ⅰ)函数的定义域为
设切点为 或
(舍去)...........3 分
...........................................................................................5
分
(Ⅱ)由 得 在 上有两个不同的实根,
设
, 时, ,
时, ...............................................8 分
, ,
,得
...............................................................10 分
( ) ( )ZkkxkZkkxk ∈≤≤+−∴∈≤≤+− ,2,222 ππππππ
( )Zkkk ∈
+− πππ
,2
( ) ,134cos2
1
3,3
2
346,12,34cos2 ≤
−≤−∴
−∈−∴
−∈
−= πππππππ
xxxxxg
( )+∞,0
( )( )00 , xfx ( )
2
1 x
xxf −=′ 2022
1
2
1
00
2
0
0
0
=∴=−−∴−=−∴ xxxx
x
10 −=x
( )12ln,2 −∴切点为
2ln22
112ln =∴+×−=−∴ mm
bxxxf ++−=
2
3
2
1)( 2 0ln2
3
4
1 2 =−+− bxxx [ ]4,1
[ ]4,1,ln2
3
4
1)( 2 ∈+−= xxxxxg
x
xxxg 2
)1)(2()(
−−=′ [ )2,1∈x 0)( <′ xg ( ]4,2∈x
0)( >′ xg
22ln)2()( min −== gxg 22ln2)4(,4
5)1( −=−= gg
0)4ln43(4
12ln24
3)4()1( <−=−=− gg
)4()1( gg <
.....12 分
20.(本小题满分 12 分)
................................................
...4 分
.......................................................
..6 分
..........
....8 分
..........................
....11 分
....................................................................
....12 分
21. (本小题满分 12 分)
解 : ( Ⅰ )
( ) [ ] .412
1
4
5,22ln 上恰有两个不等的实根,在使得方程存在实数 bxxfb +−=
−−∈∴
( ) ( ) { }为等比数列数列 2322321 11 +∴=++=++ nnn aaaa
233332 1 −=∴=•=+∴ − n
n
nn
n aa
( ) nn
nb 32 =
nn
nS 33
3
3
2
3
1
32
++++=∴
1432 33
3
3
2
3
1
3
1
+++++=∴ nn
nS
11132 33
1
2
1
2
1
3
3
11
3
113
1
33
1
3
1
3
1
3
1
3
2
+++ −
−=−
−
−
=−++++=∴ n
n
n
n
nnn
nnnS
n
n
nS
+−=∴
3
1
24
3
4
3
{ }
3
103
1
1n11n =≥∴∴>+=− ++ SSSnSS nnn 为递增数列数列
4
3
3
1 <≤∴ nS
( )
32cos2
1cos02cos3cos21cos31cos2 22 π=∴−==∴=−+∴=+− BBBBBBB 舍去或
...............................................................................
.............4 分
( Ⅱ )
.............
.......6 分
....................
.............8 分
...........................
..............10 分
.............
...............12
22、(本小题满分 12 分)
解:(1) ;......................................2 分
.................................................................................
.........5 分
(2)证明:当 时,由于 ,所以 ;
( )
4
15
4
11sin4
1
422
6242cos
2222
=
−−=∠∴−=××
−+=∠ ADCADC
;4
15sinsin;4
1coscos =∠=∠=∠−=∠∴ ADCBDCADCBDC
;8
315
2
3
4
1
2
1
4
15
3sincos3cossin3sinsin
+=×
−−×=•∠−•∠=
−∠=∠ πππ
ADCADCADCBCD又
2
15
8
315
2
3
2
sinsin
+=+×=∴∠=∠ BDB
CD
BCD
BD
.8
1535
4
1522
15
2
1sin2
1 +=××+×=∠•••=∴ ∆ BDCCDBDS BCD
同理,当 时, 。
易证 在 单调递增,在 单调递减
当 时 , 不 妨 设 , 可 知
。....................7
下面证明: ,即证
此 不 等 式 等 价 于 , 构 造 函 数
,.....................9
则 。
当 单调递减,从而 即
,所以 得证。
而 ,又 ,所以[]
。
由于 在 单调递增,所以 ,即
。..............12