- 2021-06-25 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届宁夏银川唐徕回民中学高三第一次模拟考试(2018
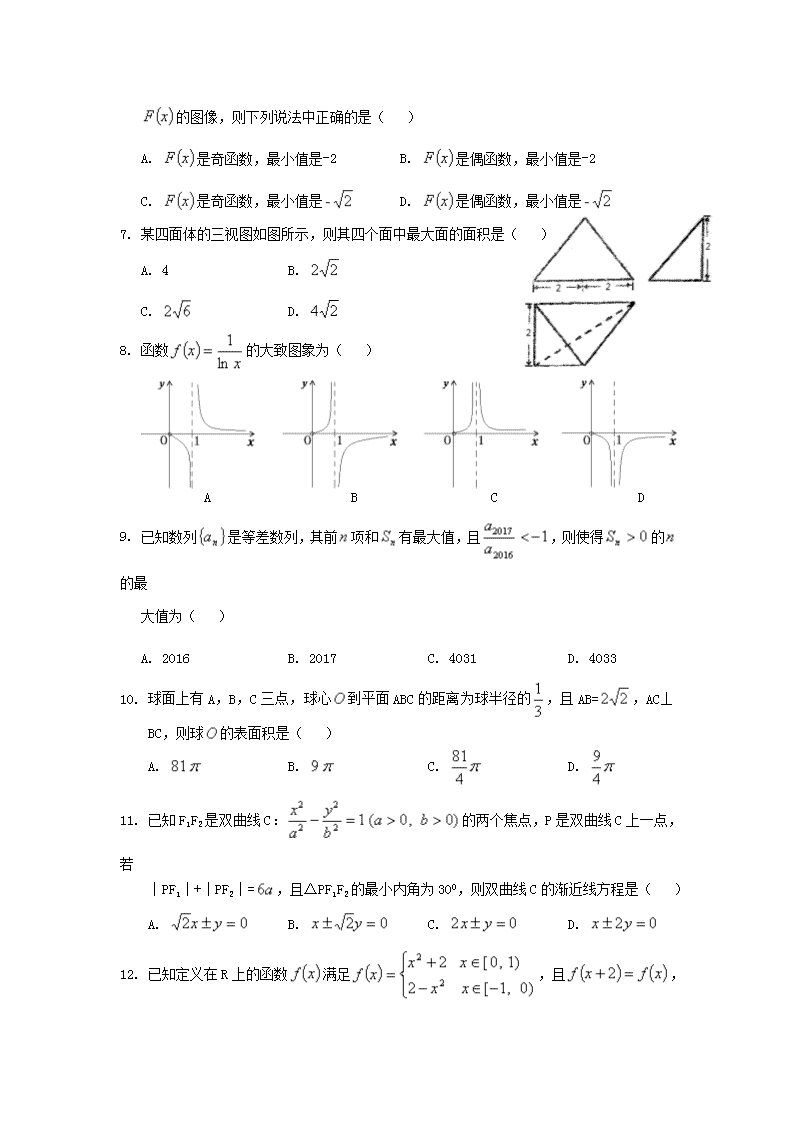
银川唐徕回民中学 2017~2018 学年度高三年级第一次模拟考试 文 科 数 学 第Ⅰ卷 一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。在每小题列出的四个 选项中, 选出符合题目要求的一项。 1. i是虚数单位,则 432 iiii ( ) A. 0 B. i C. 2 i D. -1 2. 已知集合 A={ x| 1242 xxx },B={ x| 82 1 x },则 A∩B=( ) A. { x| 4x } B. { x| 4x } C. { x| 2-x } D. { x| 2x } 3. 已知函数 112 12 )( 2 x xx xf x ,则函数 xf 的值域为( ) A.[-1,+ ) B.(-1,+) C. [ 2 1 ,+ ) D. R 4. 下面四个残差图中可反映出回归模型拟合精度较好的为( ) A B C D 5. 执行右图的程序框图,若输入的 kba ,, 分别为 1,2,3, 则输出的 M等于( ) A. 8 15 B. 5 16 C. 2 7 D. 3 20 6. 将函数 xf = -2cos x x2sin 的图像向左平移 8 个单位后得到函数 xF 的图像,则下列说法中正确的是( ) A. xF 是奇函数,最小值是-2 B. xF 是偶函数,最小值是-2 C. xF 是奇函数,最小值是 2- D. xF 是偶函数,最小值是 2- 7. 某四面体的三视图如图所示,则其四个面中最大面的面积是( ) A. 4 B. 22 C. 62 D. 24 8. 函数 x xf ln 1 的大致图象为( ) A B C D 9. 已知数列 na 是等差数列,其前n项和 nS 有最大值,且 1 2016 2017 a a ,则使得 0nS 的n 的最 大值为( ) A. 2016 B. 2017 C. 4031 D. 4033 10. 球面上有 A,B,C 三点,球心O到平面 ABC 的距离为球半径的 3 1 ,且 AB= 22 ,AC⊥ BC,则球O的表面积是( ) A. 81 B. 9 C. 4 81 D. 4 9 11. 已知 F1F2是双曲线 C: )0,0(12 2 2 2 ba b y a x 的两个焦点,P是双曲线 C上一点, 若 |PF1|+|PF2|= a6 ,且△PF1F2的最小内角为 30 0 ,则双曲线 C 的渐近线方程是( ) A. 02 yx B. 02 yx C. 02 yx D. 02 yx 12. 已知定义在 R 上的函数 xf 满足 )0,1[2 )1,0[2 2 2 xx xx xf ,且 xfxf 2 , 2 52 x xxg ,则方程 xgxf 在区间[-6,2]上所有实根之和为( ) A. -5 B. -7 C. -9 D. -11 第Ⅱ卷 二、填空题(本大题共 4 小题,每小题 5分,共 20分) 13.数列 na 是等比数列,满足 22 a , 14642 aaa ,则 6a =_________. 14. 已知实数 yx , 满足条件 1 022 x yx yx ,则 xyZ 2 的最小值是_________. 15. 若非零向量 a与b满足| a|=| a +b|=2,|b|=1,则向量 a与b夹角的余弦值为 ______. 16. 有甲、乙二人去看望高中数学张老师,期间他们做了一个游戏,张老师的生日是m月 n 日,张老师把m告诉了甲,把 n告诉了乙,然后张老师列出如下 10 个日期供选择:2 月 5 日、2 月 7日,2 月 9 日、5月 5 日、5 月 8日、8 月 4 日、8 月 7 日、9 月 4 日、9 月 6 日、9 月 9 日. 看完日期后,甲说“我不知道,但你一定也不知道”;乙听了甲的 话后说“本来我不知道,但现在我知道了”;甲接着说“哦,现在我也知道了”. 请问, 张老师的生日是_________. 三、解答题(本大题共5小题,共70分。解答应写出文字说明、证明过程或演算 步骤) 17.(本小题满分 12 分) 如图,在四边形 ABCD 中,AB=5,BC=7,AC=8,CD=6,BC⊥CD, (1)求∠BAC 的大小; (2)求四边形 ABCD 的面积. 18.(本小题满分 12 分) 某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限为 6 个月、12 个月、 18 个月、24 个月、36 个月五种. 对于这五种期限的贷款政府分别补贴 200 元、300 元、300 元、400 元、400 元. 从 2017 年享受此项政策的自主创业人员中抽取 100 人进行调查统计, 选取贷款期限的额数如下表: 贷款期限 6个月 12 个月 18 个月 24 个月 36 个月 频数 20 40 20 10 10 以上表中各种贷款期限的频率做为 2018 年自主创业选择各种贷款期限的概率. (1)若小王准备申请此次贷款,求其获得政府补贴不超过 300 元的概率; (2)若小王和小李同时申报此项贷款,求两人所获得政府补贴之和不超过 600 元的概率. 19.(本小题满分 12 分) 如图,四棱柱 ABCD—A1B1C1D1中,底面 ABCD 为菱形,AA1⊥平面 ABCD,E 为 B1D 的中点; (1)证明:平面 ACE⊥平面 ABCD; (2)若 AA1=AB=1,点 C 到平面 AED 距离为 2 2 ,求三棱锥 C—AED 的体积. 20.(本小题满分 12 分) 如图,在矩形 ABCD 中,|AB|=4,|AD|=2,O 为 AB 的中点,P、Q 分别是 AD 和 CD 的中点,且直线 AQ 与 BP 的交点在椭圆 E: )0(12 2 2 ay a x 上. (1)求椭圆 E 的方程; (2)设 R为椭圆 E 的右顶点,T 为椭圆 E的上顶点,M 为椭圆 E 第一象限部分上的一点,求四边形 ORMT 的面积 的最大值. 21.(本小题满分 12 分) 已知函数 ax x xaxf 21ln)-2 ( , (1)当 2a 时,求函数 xf 的极值; (2)当 0a 时,讨论函数 xf 的单调性; (3)若对 a (-3,-2), 21 , xx [1,3]恒有 |)()(|3ln2)3ln( 21 xfxfam 成立,求实数m的取值范围. 请考生在第 22、23 两题中任选一题做答,如果多做,则按所做的第一题记 分.答时用 2B 铅笔在答题卡上把所选题目的题号涂黑.(10 分) 22.(10 分)选修 4-4:坐标系与参数方程 在平面直角坐角系中,以原点 O为极点,x轴的正半轴为极轴建立极坐标系,曲线 1C 的 极坐标方程为 4)sin31( 22 , 2C : sin2 cos22 y x (为参数). (1)求曲线 1C 的直角坐标方程和 2C 的普通方程; (2)极坐标中两点 A( 1 , 0 ),B( 2 , 20 )都在曲线 1C 上,求 2 2 2 1 11 的 值. 23.(10 分)选修 4-5:不等式选讲 已知函数 42 axxxf , |1||1| xxxg , (1)当 1a 时,求不等式 xgxf 的解集; (2)若 cba ,, 均为正实数,且满足 3 cba ,求证: 3 222 c a b c a b .查看更多