- 2021-06-24 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湖北省沙市中学2020届高三上学期第四次双周练数学试题
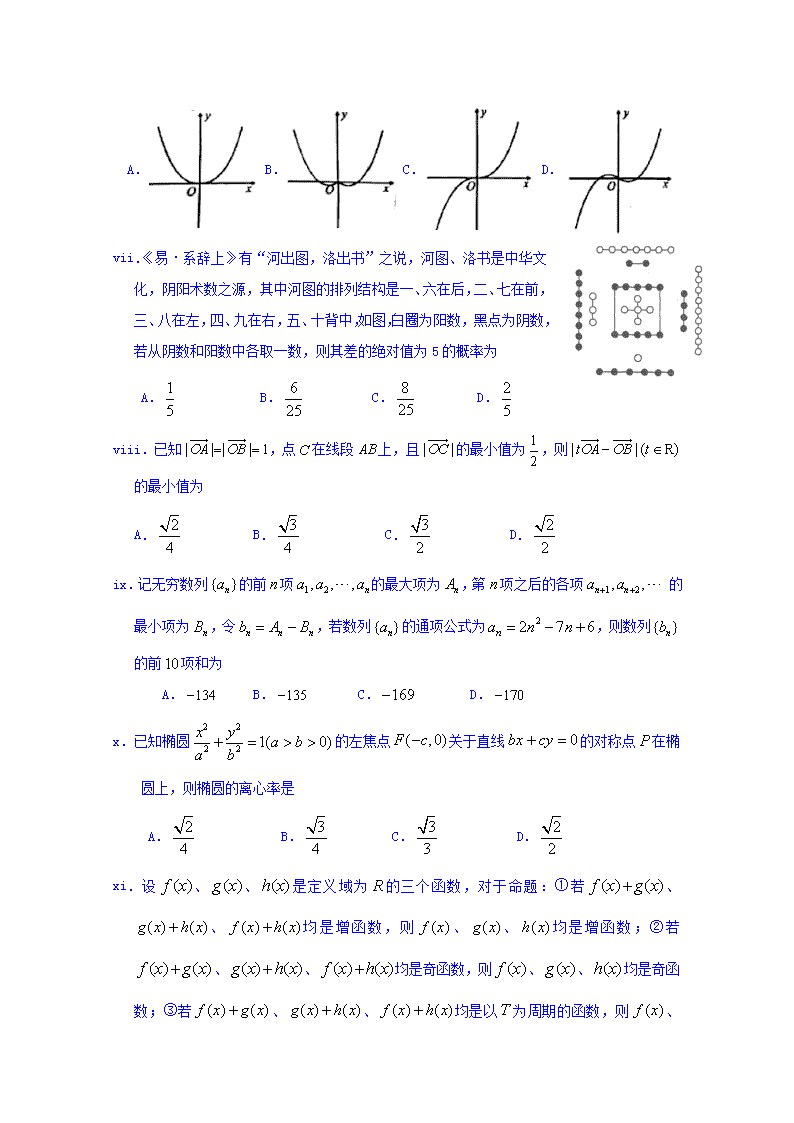
2019—2020学年上学期2017级 第四次双周练数学试卷 命题人:高三数学命题组 考试时间:2019年11月28日 一、选择题(60分) 高三年级第四次双周练数学答案 .C .已知集合,,则 A. B. C. D. .B .设,,则 A. B. C. D. .D 【解析】本题考查指数函数和对数函数的性质.由-1<c<0得0<|c|<1,又a>b>1, ∴<<0, ->->0, a>b>1>0,∴-a>-b, 即b>a.故选D. .若,则 A. B. C. D. .A .将函数的图象向 个单位长度可以得到函数的图象. A.左平移 B.左平移 C.右平移 D.右平移 .A 解析:设水深为x尺,则x2+62 =(x+2)2,解得,x=8 . ∴水深为8 尺,芦苇长为10 尺, 以AB 所在的直线为x 轴,芦苇所在的直线为y 轴, 建立如图所示的平面直角坐标系,在牵引过程中, P的轨迹是以O为圆心,半径为10 的圆弧,其方程为 x2 +y2=100(-6≤x≤6,8≤y≤10),① E点的坐标为(- 4,8),∴OE所在的直线方程为 y=- 2x,② 设Q点坐标为(x,y),由①②联立解得 x=-2,DG=6-2≈1.53 故点Q在水面上的投影离水岸边点D的的距离为1.53. .中国古代《九章算术》中有一个“引葭赴岸”问题。根据该问题我们改编一题:今有边长为尺的正方形水池的中央生长着芦苇,长出水面的部分为尺,将芦苇牵引向池岸,恰巧与水岸齐接。如图,记正方形水池的剖面图为矩形ABCD,芦苇根部为池底AB的中点,顶端为(注:芦苇与水面垂直),在牵引顶端向水岸边点D的过程中,当芦苇经过DF的三等分点E(靠近D点)时,设芦苇的顶端为Q,则点Q在水面上的投影离水岸边点D的距离为____尺. (注: ≈2.236, ≈1.732, 精确到0.01尺) A. B. C. D. .C .已知函数,是的导函数,则函数的图像大致为 A. B. C. D. .A【详解】因为阳数:,阴数:,所以从阴数和阳数中各取一数差的绝对值有:个,满足差的绝对值为5的有:共个,则. 故选:A. .《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为5的概率为 A. B. C. D. .C .已知,点在线段上,且的最小值为,则的最小值为 A. B. C. D. .C 解析:∵数列从起单调递增,且,所以,,∴。 .记无穷数列的前项的最大项为,第项之后的各项 的最小项为,令,若数列的通项公式为,则数列的前项和为 A. B. C. D. .D .已知椭圆的左焦点关于直线的对称点在椭圆上,则椭圆的离心率是 A. B. C. D. . D 可设,均为增函数,符合、、均是增函数,说明①错误。 .设、、是定义域为的三个函数,对于命题:①若、、均是增函数,则、、均是增函数;②若、、均是奇函数,则、、均是奇函数;③若、、均是以为周期的函数,则、 、均是以为周期的函数。下列正确的是 A.①、②、③均为真命题 B.①、②均为假命题,③为真命题 C.①、③为真命题,②为假命题 D.①为假命题,②、③为真命题 .D .四面体的四个顶点都在球的表面上,,,,分别是的中点,且,,则球的体积为 A. B. C. D. 二、填空题(20分) . .曲线在处的切线方程为 . .-10【解析】本题考查等比数列的性质及等差数列求和公式.由于{an}是正项等比数列,设an=a1qn-1,其中a1是首项,q是公比. 则,解得 .故an=2n-5,∴= =(-4)+(-3)+…+(n-5)= n(n-9)= [(n-)2- ],∴当n=4或5时, 取最小值-10. .设等比数列满足且,, 则的最小值为 . . .从图中所示的矩形区域内任取一点,则点取自阴影 部分的概率为 . .3, 解:设,则,∴,中,∴,又∵,∴,所以渐近线方程为。 .已知双曲线的左右焦点为,右支上一点与的连线交双曲线左支于点,若,则的面积为 ,此双曲线的渐近线方程为 . 三、解答题(70分) .(1), ∴或 即 或 ∵是三角形内角,∴或,故是等腰三角形或直角三角形; (2)为锐角三角形,∴,又,设为中点 故在△中,, ∴.进一步可得 .在中,分别为角所对的边,若. (Ⅰ)试判断的形状; (Ⅱ)若为锐角三角形,且,求角的正切值. .(19年浙江19题改编)解:(Ⅰ)连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC. 又平面A1ACC1⊥平面ABC,A1E平面A1ACC1, 平面A1ACC1∩平面ABC=AC,所以,A1E⊥平面ABC. ……………2分 ∴. 解法一:又∵,故.∴平面. ……………4分 ∴.……………5分 (2)取的中点,连接,则是平行四边形. 连接交于,则是的中点. 由于A1E⊥平面ABC,,故平行四边形是矩形. ……………7分 由(1)知平面,∴平面平面且交于, ∴在平面上的射影在直线上, 则是直线与平面所成角(或其补角). ……………8分 设直线与平面所成角为,则,设,则, ,,,∴ ①当时,,△中,由余弦定理可解得:, 则,∴,; ……………10分 ②当时,,由余弦定理可解得:, 则,∴,; ……………11分 综合①②可知,或 ………………………12分 解法二:取中点为原点,直线为轴,射线为轴正半轴,建立空间直角坐标系.(也可以:以为原点,为轴,或者以为轴,为轴), 则,设 由得 ………………………3分 , ………………………5分 (Ⅱ)由(1)知,设平面的法向量为 那么,令,得 ………………………8分 依题意, 化简得,解得或 ………………………11分 或 ………………………12分 .如图,已知三棱柱中,平面平面,,,,,分别是的中点. (Ⅰ)证明:; (Ⅱ)若直线与平面所成角的正弦值为,求的长。 .(1),, ,, ∴,∴可用线性回归模型拟合. (2)当时,利润:(元), 当时,利润:(元), 当时,利润:(元) ∴周总利润平均值为:(元) .某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.过去的50周资料显示,该地周光照量(单位:小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量(千克)与使用某种液体肥料的质量(千克)之间的对应数据为下表: (千克) 2 4 5 6 8 (千克) 3 4 4 4 5 (Ⅰ)依据此表计算相关系数(精确到),并据此判断是否可用线性回归模型拟合与的关系.(若,则线性相关很高,可用线性回归模型拟合) (Ⅱ)蔬菜大棚对光照要求较高,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量的限制,并有如下关系: 周光照量/小时 光照控制仪运行台数 3 2 1 对商家来说,若某台光照控制仪运行,则该台光照控制仪产生的周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去的50周的周总利润的平均值. 相关系数公式:,参考数据:. .(1)F(,0),直线AB的方程为:. 联立方程组,可得:, 设A(x1,y1),B(x2,y2),则, ∴(,p),(0,p),直线的方程为y=﹣x.∴C(,0), ∴四边形为梯形,其面积为 ∴p=2,即抛物线E的方程为:y2=4x. (2)证明:设直线的方程为,抛物线联立可得,,解得:,代入的方程,化简后可得,将点M,N的横坐标分别代入直线, 得M(1,),N(﹣1,), ∵F(1,0),∴,|NF|=, ∴,∴点P在抛物线上移动时,恒为定值1. .如图1,已知抛物线:的焦点为,过且斜率为直线交于两点,线段 的中点为,其垂直平分线交轴于点,轴于点,四边形的面积等于7. (Ⅰ)求的方程; (Ⅱ)如图2,设直线为抛物线的准线,直线是抛物线的通径所在的直线,过上一点()()作直线与抛物线相切,若直线与直线相交于点,与直线相交于点,证明:点在抛物线上移动时,恒为定值,并求出此定值. 图1 图2 .(I), ………………2分 , 在点处的切线方程为. ………………………4分 (Ⅱ)令,则为偶函数 ∵时, ………………6分 (1)当时,,不合题意 …………………………………8分 (2)当时,,则, 令则,故在上单调递增, 又∵,∴ 在上恒成立,即在上单调递增, 又∵,∴在上恒成立, 满足题意 ………………10分 (3)当时,∵, 由(2)知恒成立, 综上, 的取值范围为 …………………………………12分 .已知函数. (Ⅰ)若曲线在点处的切线的斜率为,求曲线在点处的切线方程; (Ⅱ)若恒成立,求的取值范围. 选考题 请考生从以下两题中任选一题作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑,注意所做题目的题号必须与所涂题号一致,如果多做,则按所做的第一题计分。(12分) .【详解】(1)将的参数方程化为普通方程得,将 代入,并化简得C的极坐标方程为. 的极坐标方程为 (2)依题意可得点的极坐标为,即 ,即 因为,所以,当时,取得最大值. .(本小题满分10分)选修4-4:坐标系与参数方程 在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为,将直线绕极点逆时针旋转个单位得到直线. (Ⅰ)求和的极坐标方程; (Ⅱ)设直线和曲线交于两点,直线和曲线交于两点,求的最大值. .(本小题满分10分)选修4—5:不等式选讲 解:(Ⅰ)不等式的解集为或. …………5分 (Ⅱ).…………7分 ∵,∴在上单调递减,在和上单调递增 ∴当时取得最小值,…………9分 ∴,所以或, ∵,∴为所求实数的取值范围. ……………10分 .(本小题满分10分)选修4-5:不等式选讲 已知函数. (Ⅰ)当时,求不等式的解集; (Ⅱ)若,且对任意,,求实数的取值范围.查看更多