- 2021-06-23 发布 |
- 37.5 KB |
- 36页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西专版2020中考数学复习方案第五单元四边形第21课时多边形与平行四边形课件
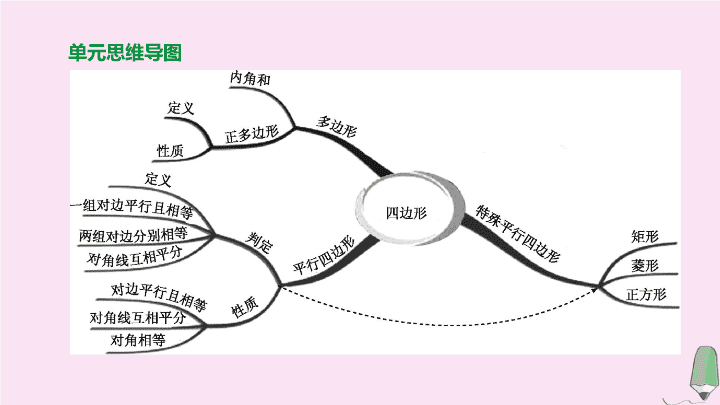
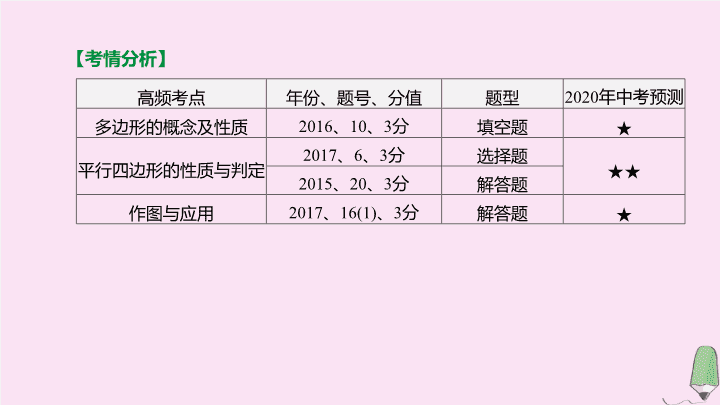
单元思维导图 第 21 课时 多边形与平行四边形 第五单元 四边形 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 多边形 的概念 及性质 2016 、 10 、 3 分 填空题 ★ 平行四边形 的性质 与判定 2017 、 6 、 3 分 选择题 ★★ 2015 、 20 、 3 分 解答题 作图与应用 2017 、 16(1) 、 3 分 解答题 ★ 图形 性质 多 边 形 内角和 n 边形的内角和为 ① 外角和 任意多边形的外角和为 360° 对角线 (1) n 边形共有 ② 条对角线 ; (2) 从一个顶点出发的对角线把 n 边形分成 ③ 个三角形 不稳定性 n 边形 ( n> 3) 具有不稳定性 考点一 多边形 考点聚焦 ( n -2)·180° ( n -2) 图形 性质 正 多 边 形 边 各条边 ④ 内角 各个内角 ⑤ , 且正 n 边形的每个内角为 ⑥ 外角 各个外角相等 , 且正 n 边形的每个外角为 ⑦ 对称性 (1) 正多边形都是 ⑧ 对称图形 , 其中边数为偶数的正多边形也是中心对称图形 ; (2) 正 n 边形有 ⑨ 条对称轴 ( 续表 ) 相等 相等 轴 n 定义 两组对边分别平行的四边形是平行四边形 性质 (1) 平行四边形的对边 ⑩ ; (2) 平行四边形的对角 ⑪ , 邻角 ⑫ ; (3) 平行四边形的对角线互相 ⑬ ; (4) 平行四边形是 ⑭ 对称图形 考点二 平行四边形 平行且相等 相等 互补 平分 中心 ( 续表 ) 判定 (1) 两组对边分别平行的四边形是平行四边形 ; (2) 两组对边分别 ⑮ 的四边形是平行四边形 ; (3) 一组对边 ⑯ 的四边形是平行四边形 ; (4) 两组对角分别 ⑰ 的四边形是平行四边形 ; (5) 对角线互相 ⑱ 的四边形是平行四边形 面积 S=ah ( a 表示一条边长 , h 表示此边上的高 ) 相等 平行且相等 相等 平分 【 温馨提示 】 (1) 平行四边形的两条对角线将平行四边形分成 ⑲ 的四个三角形 ; (2) 同底等高的平行四边形的面积相等 ; (3) 若一条直线过平行四边形的对角线的交点 , 则这条直线平分平行四边形的面积 面积相等 题组一 必会题 对点演练 1 . 如图 21-1, 足球图片中的黑色正五边形的内角和是 ( ) A . 180° B . 360° C . 540° D . 720° C 图 21-1 2 . [2019· 泸州 ] 四边形 ABCD 的对角线 AC 与 BD 相交于点 O , 下列四组条件中 , 一定能判定四边形 ABCD 为平行四边形的是 ( ) A .AD ∥ BC B .OA=OC , OB=OD C .AD ∥ BC , AB=DC D .AC ⊥ BD B 3 . [2019· 遂宁 ] 如图 21-2,▱ ABCD 中 , 对角线 AC , BD 相交于点 O , OE ⊥ BD 交 AD 于点 E , 连接 BE , 若 ▱ ABCD 的周长为 28, 则 △ ABE 的周长为 ( ) A . 28 B . 24 C . 21 D . 14 图 21-2 [ 答案 ] D [ 解析 ] ∵四边形 ABCD 是平行四边形 , ∴ OB=OD , AB=CD , AD=BC. ∵平行四边形的周长为 28, ∴ AB + AD= 14 . ∵ OE ⊥ BD , ∴ OE 是线段 BD 的中垂线 , ∴ BE=ED , ∴ △ ABE 的周长 =AB + BE + AE=AB + AD= 14 . 故选 D . 4 . [2019· 株洲 ] 如图 21-3, 过正五边形 ABCDE 的顶点 B 作一条射线与其内角∠ EAB 的平分线相交于点 P , 且∠ ABP= 60°, 则∠ APB= 度 . 图 21-3 [ 答案 ] 66 [ 解析 ] ∵五边形 ABCDE 为正五边形 , ∴∠ EAB= 108° . ∵ AP 是∠ EAB 的平分线 , ∴∠ PAB= 54° . ∵∠ ABP= 60°, ∴∠ APB= 180°-60°-54° = 66° . 故答案为 :66 . 5 . [2019· 徐州 ] 如图 21-4, A , B , C , D 为一个外角为 40° 的正多边形的顶点 . 若 O 为正多边形的中心 , 则∠ OAD= ° . 图 21-4 [ 答案 ] 30 题组二 易错题 【 失分点 】 平行四边形的性质模糊 , 不能准确、恰当地运用性质解决问题 ; 理不清平行四边形判定的依据 ; 忽视分类讨论导致漏解 . 6 . 如图 21-5, 在四边形 ABCD 中 , AB ∥ CD , AD ∥ BC , 现在请你添加一个适当的条件 : , 使得四边形 AECF 为平行四边形 ( 图中不再添加字母和线 ) . 图 21-5 [ 答案 ] BE=DF ( 答案不唯一 ) [ 解析 ] ∵四边形 ABCD 为平行四边形 , ∴ AB=CD , ∠ ABE= ∠ CDF. 又∵ BE=DF , ∴ △ ABE ≌△ CDF , ∴ AE=CF , ∠ AEB= ∠ CFD , ∴∠ AEF= ∠ EFC , ∴ AE ∥ FC , ∴四边形 AECF 为平行四边形 . [ 答案 ] 12 或 20 考向一 与多边形有关的计算 例 1 如图 21-6, 已知正五边形 ABCDE , AF ∥ CD 交 DB 的延长线于点 F , 交 DE 的延长线于点 G. (1) 求∠ F 的度数 ; (2) 写出图中的等腰三角形 . 图 21-6 解 :(1) ∵五边形 ABCDE 是正五边形 , ∴∠ DCB= ∠ EDC= 108°, DC=BC , ∴∠ CDB= 36° . ∵ AF ∥ CD , ∴∠ F= ∠ CDB= 36° . 例 1 如图 21-6, 已知正五边形 ABCDE , AF ∥ CD 交 DB 的延长线于点 F , 交 DE 的延长线于点 G. (2) 写出图中的等腰三角形 . 图 21-6 (2) 等腰三角形有 △ BCD ,△ DGF , △ ABF ,△ AEG. | 考向精练 | 1 . 若正多边形的一个外角是 60°, 则这个正多边形的内角和是 . 720° 2 . [2019· 枣庄 ] 用一条宽度相等的足够长的纸条打一个结 ( 如图 21-7 ①所示 ), 然后轻轻拉紧、压平就可以得到如图 21-7 ②所示的正五边形 ABCDE. 图中 , ∠ BAC= ° . [ 答案 ] 36 图 21-7 考向二 平行四边形的性质及判定 图 21-8 例 2 [2019· 福建 ] 在 Rt△ ABC 中 , ∠ ABC= 90°, ∠ ACB= 30° . 将 △ ABC 绕点 C 顺时针旋转一个角度 α 得到 △ DEC , 点 A , B 的对应点分别为 D , E. (1) 若点 E 恰好落在边 AC 上 , 如图 21-8 ① , 求∠ ADE 的大小 ; (2) 若 α= 60°, F 为 AC 的中点 , 如图 21-8 ② , 求证 : 四边形 BEDF 是平行四边形 . 图 21-8 例 2 [2019· 福建 ] 在 Rt△ ABC 中 , ∠ ABC= 90°, ∠ ACB= 30° . 将 △ ABC 绕点 C 顺时针旋转一个角度 α 得到 △ DEC , 点 A , B 的对应点分别为 D , E. (2) 若 α= 60°, F 为 AC 的中点 , 如图 21-8 ② , 求证 : 四边形 BEDF 是平行四边形 . 【 方法点析 】 (1) 平行四边形的性质都是通过连接对角线把四边形问题转化成三角形问题来处理的 . 常应用平行四边形的性质解决某些问题 , 如计算角的度数 , 线段的长度 , 证明两线平行、线段相等以及角相等 . | 考向精练 | 1 . [2015· 江西 5 题 ] 如图 21-9, 小贤为了体验四边形的不稳定性 , 将四根木条用钉子钉成一个矩形框架 ABCD , B 与 D 两点之间用一根橡皮筋拉直固定 , 然后向右扭动框架 , 观察所得四边形的变化 , 下列判断错误的是 ( ) A . 四边形 ABCD 由矩形变为平行四边形 B .BD 的长度增大 C . 四边形 ABCD 的面积不变 D . 四边形 ABCD 的周长不变 图 21-9 [ 答案 ] C [ 解析 ]A 选项 , 在扭动过程中 , 矩形两组对边的长度没有变化 , 则四边形 ABCD 仍是平行四边形 , 正确 ;B 选项 , 向右扭动的过程中 , BD 的长度增大 , 正确 ;C 选项 , 向右扭动的过程中 , 底边 BC 不变 , 但平行四边形边 BC 上的高在变化 , 则面积变化 , 错误 ; D 选项 , 矩形在扭动过程中 , 两组对边的长度没有变化 , 故四边形 ABCD 的周长不变 , 正确 . 故选 C . 2 . [2016· 江西 10 题 ] 如图 21-10, 在平行四边形 ABCD 中 , ∠ C= 40°, 过点 D 作 AD 的垂线 , 交 AB 于点 E , 交 CB 的延长线于点 F , 则∠ BEF 的度数为 . [ 答案 ] 50° [ 解析 ] ∵四边形 ABCD 是平行四边形 , ∴ DC ∥ AB , ∴∠ C= ∠ ABF. 又∵∠ C= 40°, ∴∠ ABF= 40° . ∵ EF ⊥ AD , AD ∥ BF , ∴ EF ⊥ BF , ∴∠ F= 90°, ∴∠ BEF= 90°-40° = 50° . 图 21-10 3 . [2019· 南昌十校联考 ] 如图 21-11, 在 ▱ ABCD 中 , 点 E 在边 DC 上 ,△ DEF 的面积与 △ BAF 的面积之比为 9 ∶ 16, 则 EC ∶ AB= . 图 21-11 [ 答案 ] 1 ∶ 4 考向三 与多边形及平行四边形有关的作图与应用 例 3 [2019· 赣北联考 ] 如图 21-12, 在 ▱ ABCD 中 , 点 E 为边 BC 上的中点 , 请仅用无刻度的直尺 , 按要求画图 ( 保留画图痕迹 , 不写画法 ) . (1) 在图 21-12 ①中 , 作 EF ∥ AB 交 AD 于点 F ; (2) 在图 21-12 ②中 , 若 AB=BC , 作一矩形 , 使得其面积等于 ABCD 的一半 . 图 21-12 解 :(1) 如图① , F 点就是所求作的点 . (2) 如图② , 矩形 EGFH 就是所求作的四边形 . | 考向精练 | 图 21-13 [2017· 江西 16 题 ] 如图 21-13, 已知正七边形 ABCDEFG , 请仅用无刻度的直尺 , 分别按下列要求画图 . (1) 在图 21-13 ①中 , 画出一个以 AB 为边的平行四边形 ; (2) 在图 21-13 ②中 , 画出一个以 AF 为边的菱形 . 解 :(1) 如图 . 四边形 ABHF 是平行四边形 , 四边形 ABHI 是平行四边形 . 图 21-13 [2017· 江西 16 题 ] 如图 21-13, 已知正七边形 ABCDEFG , 请仅用无刻度的直尺 , 分别按下列要求画图 . (2) 在图 21-13 ②中 , 画出一个以 AF 为边的菱形 . (2) 如图 . 四边形 AHDF 是菱形 , 四边形 ACHF 是菱形 .查看更多