- 2021-06-23 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考总复习 圆
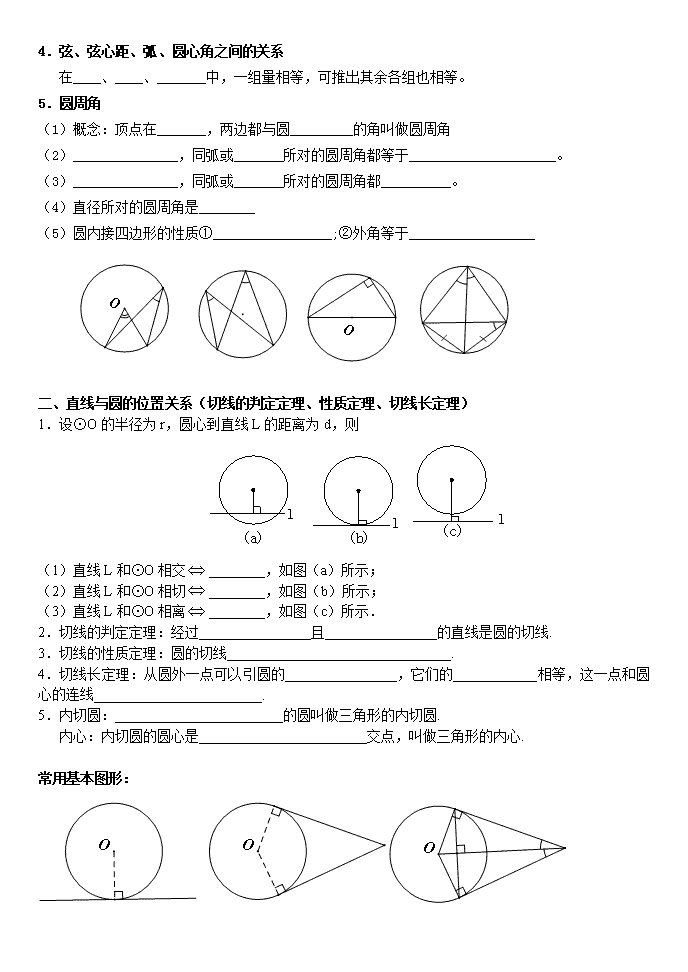
北京市西城区重点中学2016年3月初三数学中考复习 《圆》复习建议讲义及练习 一、2016年中考说明 考试内容 考试要求 A B C 图形与几何 图 形 的 性 质 圆的有关概念 理解圆、弧、弦、圆心角、圆周角的概念;了解等圆、等弧的概念 能利用圆的有关概念解决有关简单问题 圆的有关性质 了解弧、弦、圆心角的关系,理解圆周角与圆心角及其所对弧的关系 能利用垂径定理解决有关简单问题;能利用圆周角定理及其推论解决有关简单问题 运用圆的性质的有关内容解决有关问题 点和圆的位置关系 了解点与圆的位置关系 尺规作图(利用基本作图完成):过不在同一直线上的三点作圆;能利用点和圆的位置关系解决有关简单问题 直线与圆的位置关系 了解直线与圆的位置关系;会判断直线和圆的位置关系;理解切线与过切点的半径之间的关系;会用三角尺过圆上一点画圆的切线 掌握切线的概念;能利用切线的判定和性质解决有关简单问题;能利用直线与圆的位置关系解决简单问题;能利用切线长定理解决有关简单问题 运用圆的切线的有关内容解决有关问题 多边形和圆 了解圆内接多边形和多边形外接圆的概念;了解三角形外心的概念;知道三角形的内切圆;了解三角形的内心;了解正多边形的概念及正多边形与圆的关系 能利用圆内接四边形的对角互补解决有关简单问题;能利用正多边形解决有关简单问题;尺规作图(利用基本作图完成):作三角形外接圆、内切圆,作圆的内接正方形和正六边形 弧长、扇形面积和圆锥 会计算圆的弧长和扇形面积; 会求圆锥的侧面积和全面积 能利用圆的弧长和扇形的面积解决一些简单的实际问题 二、复习建议 1.依据考试说明的要求进行复习,重点知识重点复习、知识系统复习全面、非重点的A级知识点适当安排、不漏过,不随意拔高难度;B级的知识要落实到位;C级知识要达到灵活运用; 2.培养学生的识图能力,从复杂的几何图形中拆分出常见的基本图形; 3.通过习题培养学生分析问题解决问题的能力。去模式化,重视能力的培养,重视数学思想方法的渗透; 4. 重视学生思路的收集,关注学生的学习过程,给予有效的学习方法指导. 三、课时安排 建议安排4-5课时左右 四、具体内容 基本概念复习 一、弧、弦、圆周角、圆心角 1.圆的定义: (1)描述性定义:在平面内,线段OA绕它固定的一个端点O________,另一个端点A所形成的图形叫做圆.其中,固定的端点O叫做______,线段OA叫做______,以O为圆心的圆,记作“_____”,读作“_____”. (2)集合性定义: 平面上到_________的距离等于定长r的_________是以O为______、以r为________的圆. (3)性质:同圆或________中,________________ 2.与圆有关的概念: (1)弦:连接圆上任意两点的__________叫做弦;__________的弦叫做直径. (2)弧:圆上_________________叫做圆弧,简称“弧”,用符号____表示,以A、B为端点的弧记作 __________,读作“__________ 弧的分类: 半圆:圆的任意一条________的两个端点分圆成两条弧,每条弧都叫做半圆. 优弧:______半圆的弧叫做优弧劣弧;_________半圆的弧叫做劣弧 (3)等圆:能够__________的两个圆叫做等圆. 即:半径相等的圆是等圆;同圆或等圆的半径相等. (4)等弧:在_________________中,能够__________的弧叫做等弧. (5)同心圆:__________相同,__________不相等的圆叫做同心圆. 3.垂径定理_______________________________________________ 垂径定理的推论 “平分弦(_____________)的直径_____于弦,并且_________________ 4.弦、弦心距、弧、圆心角之间的关系 在____、____、_______中,一组量相等,可推出其余各组也相等。 5.圆周角 (1)概念:顶点在_______,两边都与圆_________的角叫做圆周角 (2)_______________,同弧或_______所对的圆周角都等于_____________________。 (3)_______________,同弧或_______所对的圆周角都__________。 (4)直径所对的圆周角是________ (5)圆内接四边形的性质①_________________;②外角等于__________________ 二、直线与圆的位置关系(切线的判定定理、性质定理、切线长定理) 1.设⊙O的半径为r,圆心到直线L的距离为d,则 (1)直线L和⊙O相交________,如图(a)所示; (2)直线L和⊙O相切________,如图(b)所示; (3)直线L和⊙O相离________,如图(c)所示. 2.切线的判定定理:经过________________且________________的直线是圆的切线. 3.切线的性质定理:圆的切线________________________________. 4.切线长定理:从圆外一点可以引圆的________________,它们的____________相等,这一点和圆心的连线________________________. 5.内切圆:________________________的圆叫做三角形的内切圆. 内心:内切圆的圆心是________________________交点,叫做三角形的内心. 常用基本图形: 三、点与圆的位置关系 1.设⊙O的半径为r,点P到圆心的距离OP=d, 点P在圆外__________;点P在圆上__________;点P在圆内__________ 2.经过三角形的__________可以做一个圆,并且_______画一个圆,这个圆叫做三角形的外接圆. 外接圆的圆心是三角形_________________的交点,叫做这个三角形的_______. 三角形的外心就是三角形_________________的交点,它到________________的距离相等. 四、正多边形和圆 1、多边形的中心:一个正多边形的_________的圆心. 2、正多边形的半径:_________的半径. 3、正多边形的中心角:正多边形_________的圆心角. 4、正多边形的边心距:中心到_________的距离. 常用基本图形: 五、弧长与扇形面积、圆锥的侧面展开图 1.圆周长:C=_________ 2.弧长: 3.扇形面积:=。 4.圆锥的侧面积 5.圆锥的全面积 弧、弦、圆心角、圆周角 例1. (1).如图,AB为圆O的直径,弦CD^AB,垂足为点E,连结OC, 若 OC=5,CD=8,则AE= . (2). 如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°, OC=4,CD的长为( ) A. 2 B.4 C. 4 D.8 (3).如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( ) A. 25° B. 50° C. 60° D. 80° (4).如图,的半径为1,是的内接等边三角形,点D,E在圆上,四边形为矩形,这个矩形的面积是_______________. (5)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( ) (6)如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a 的值是( ) A. 4 B. C. D. 例2.(西城总复习 P82例1)如图,在⊙O中,弦AB的中点为C, 过点C的半径为OD. (1)若AB=,OC=1,求CD的长; (2)若半径OD=R,∠AOB=120°,求CD的长. 例3.(西城总复习 P82例2)已知:如图,⊙O中,半径OA=4, 弦BC经过半径OA的中点P,∠OPC=60°,求弦BC的长. 例4.如图,在坐标平面内,以点M(0,)为圆心,以2为半径作⊙M交x轴于A、B两点,交y轴于C、D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E点. (1)求出CP所在直线的解析式; (2)连接AC,求△ACP的面积. 例5.已知:P为等边△ABC外接圆弧BC上一点, 求证:PA=PB+PC. 练习: 1. 如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°, BC∥OD交⊙O于C,则∠A= . C H O F G E A B 2.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为 . 3.如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C. (1)求证:CB∥PD; (2)若BC=3,sin∠P=,求⊙O的直径. 直线和圆的位置关系 例1.已知Rt△ABC的斜边AB=8cm,AC=4cm. (1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切? (2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系? 例2.(西城总复习 P82例3)如图,AB为⊙O的直径,C为⊙O上一点, AD和过点C的切线互相垂直,垂足为D. (1)求证:AC平分∠DAB; (2)若∠B=60°,CD=2,求AE的长. 例3.(西城总复习 P83例4)已知:如图,AB是⊙O的直径, ∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于 点N,交BC延长线于E,直线CF交EN于F,且∠ECF=∠E. (1)求证:CF是⊙O的切线; (2)设⊙O的半径为1,且AC=CE,求MO的长. 例4.(西城总复习 P84例5)如图,AB是⊙O的弦,D为半径 OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F, O 且CE=CB. (1)求证:BC是⊙O的切线; (2)连接AF,BF,求∠ABF的度数. 例5.(西城总复习P84例6)已知:如图,⊙O的直径AB=4,点P是AB延长线上一点,PC切⊙O于点C,连结AC. ∠CPA的平分线PM交AC于点M. (1)若∠CAP=30°,求CP的长及∠CMP的度数; (2)若点P在AB的延长线上运动, 你认为∠CMP 的大小会是否发生变化?若变化,请说明理由;若不变化, 请求出∠CMP的值; (3)若点P在直径BA延长线上运动,PC切⊙O于点C, 那么∠CMP的大小会是否发生变化?请直接写出你的结论. 练习 1. (11北京)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB. (1)求证:直线BF是⊙O的切线; (2)若AB=5,sin∠CBF=,求BC和BF的长. 2. (12北京)已知:如图,是的直径,是上一点,于点,过点作的切线,交 的延长线于点,连结. (1)求证:与相切; (2)连结并延长交于点,若 ,求的长. 3. (13北京)如图,AB是⊙O的直径,PA,PC分别与⊙O 相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E. (1)求证:∠EPD=∠EDO (2)若PC=6,tan∠PDA=,求OE的长。[中国教育出&版*^#@网] 4.(14北京)如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线 BD交AC的延长线于点D,E 是OB的中点,CE的延长线交切线BD于 点F,AF交⊙O于点H,连接BH. (1)求证:AC=CD; (2)若OB=2,求BH的长. 5.(15北京)如图,AB是⊙O的直径,过点B作⊙O的切线BM, 弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交 BM于点E. (1)求证:△ACD是等边三角形; (2)连接OE,若DE=2,求OE的长. 6.(15西城一模)如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称.作BE⊥l于点E,连接AD,DE. (1)依题意补全图形; (2)在不添加新的线段的条件下,写出图中 与∠BED相等的角,并加以证明. 7.(15西城二模)如图1,AB为⊙O的直径,弦CD⊥AB于点E,点F在线段ED上.连接AF 并延长交⊙O于点G,在CD的延长线上取一点P,使PF=PG. (1)依题意补全图形,判断PG与⊙O的位置关系,并证明你的结论; (2)如图2,当E为半径OA的中点,DG∥AB,且时,求PG的长. 点和圆的位置关系 例1.已知:点P到⊙O最近的距离为3,最远的距离为11,则⊙O的半径为 . 例2.(西城总复习 P85例9)如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点. (1)使∠APB=30°的点P有_____ 个; (2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标; (3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,也请说明理由. 练习:(西城总复习P89,21,北京2013) 对于平面直角坐标系O中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得 ∠APB=60°,则称P为⊙C的关联点.已知点 D(,),E(0,-2),F(,0) (1)当⊙O的半径为1时, ①在点D,E,F中,⊙O的关联点是__________; ②过点F作直线交轴正半轴于点G,使∠GFO=30° ,若直线上的点P(,)是⊙O的关联点,求的取值范围; (2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径的取值范围. 圆中计算及作图 例1:完成下列作图 (1)过不共线的三点确定一个圆 (2)过圆上一点作已知圆的切线 (3)过圆外一点作已知圆的切线 (4)已知直线a及直线外一点P,求作:⊙P与直线a相切. (5)画△ABC的内切圆,并标出它的内心 (6)画出△DEF的外接圆,并标出它的外心; (7)作⊙O的内接正方形,内接正六边形 (8)等分圆周(三、六、十二、四、八等分) 例2.(1) 正六边形的边长a,半径R,边心距r的比a∶R∶r=_______. (2)已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度为____________,该圆弧所对扇形面积为____________. (3)半径为2的扇形,面积为,则它圆心角的度数为_________,所对弧长为__________. (4)扇形圆心角为150°,弧长为20πcm,则扇形的面积为______________. (5)钟表的轴心到分针针端的长为5cm,经过40分钟,分针针端转过的弧长为___________. 例3.(西城总复习 P85例7)如图,平地面上有一面积为30πcm2的扇形AOB,半径OA=6cm,在OA与地面垂直并且扇形没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,求点O移动的距离. 例4.(西城总复习P85例8) (1) 如图1,扇形OAB的圆心角为90度,分别以OA、OB为直径在扇形内作半圆,P和Q分别表示阴影部分的面积,那么P和Q的大小关系是( ) A. P=Q B.P>Q C.PS4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3 9. 小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上. (1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹). (1) 若△ABC中AB=8米,AC=6米,∠BAC=,试求小明家圆形花坛的面积. 10. 如图,中,,. (1)动手操作:利用尺规作以为直径的,并标出与的交点,与的交点 (保留作图痕迹,不写作法): (2)综合应用:在你所作的圆中, ①求证:;②求点到的距离. 11.如图,在长方形ABCD中,AB=3,BC=1,E在AB上,AE=2. 分别以E,B为圆心,以2为半径画圆弧交DC于F,G,交AB于A,H. (1)求四边形BEFG的面积; (2)求由弧FA和弧GH两段圆弧及线段AH,FG所围成的阴影部分面积.
查看更多