专题10 综合训练2（第02期）-2017年高考数学（文）备考之百强校大题狂练系列

专题10 综合训练2（第02期）-2017年高考数学（文）备考之百强校大题狂练系列

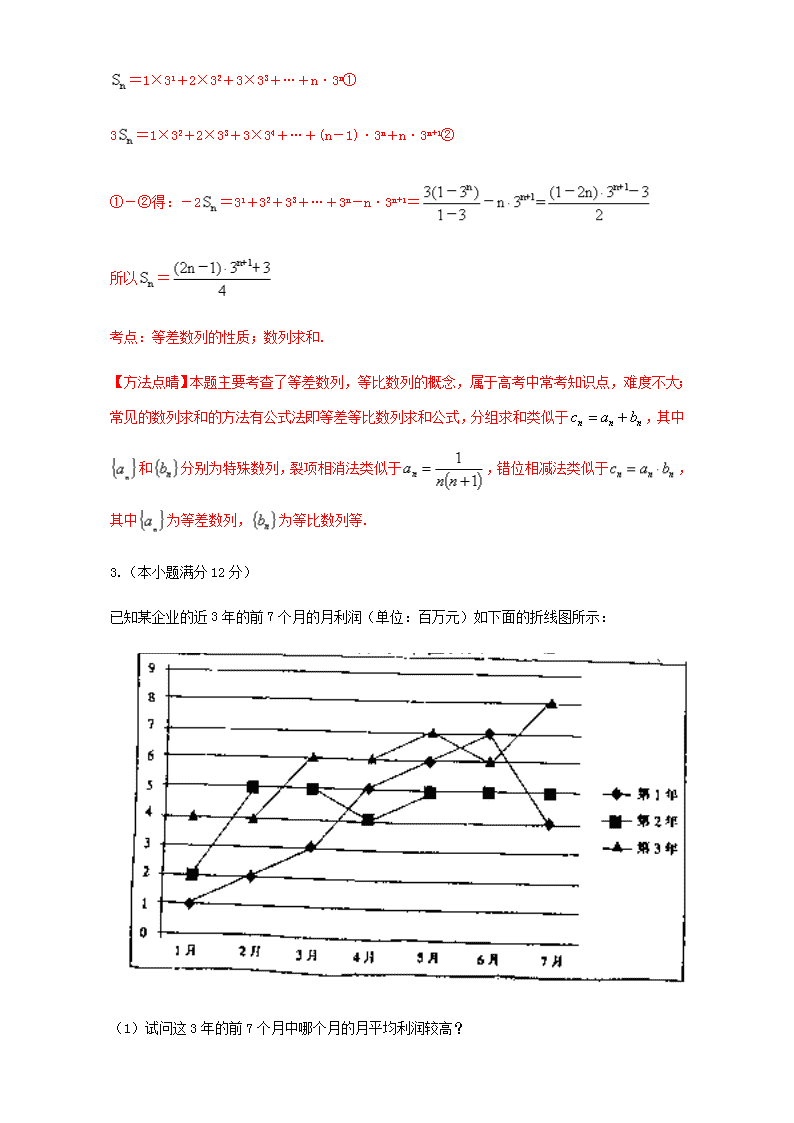
‎2017届高考数学（文）大题狂练 专题10 综合训练2‎ ‎1.（本小题满分12分）‎ 已知函数，且．‎ ‎（1）求的值；‎ ‎（2）若，求．‎ ‎【答案】(1)；(2).‎ 试题解析：（1）∵，∴，‎ ‎∵，∴，∴，解得：．．．．．．．．．．．．．4分 ‎（2）由（1）知：，∴，‎ ‎∵‎ ‎∴．．．．．．．．．．．．．．．8分 ‎∵，∴．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分 ‎∴．．．．．．．．12分 考点：1.特殊角的三角函数求值；2.两角和与差的正弦公式.‎ ‎【方法点睛】本题主要考查的是特殊角的三角函数值,两角和与差的正弦公式,同角三角函数的基本关系和三角函数的诱导公式,属于中档题.解本题需要掌握的基本公式有:等,在求三角函数值时,要注意先根据已知判断出角的范围,再确定函数值的正负.‎ ‎2．（本小题满分12分）‎ 数列满足 ‎⑴证明：数列是等差数列；‎ ‎⑵设，求数列的前项和.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎（2）由（1）得，所以＝2，从而＝·3n ‎ ‎＝1×31＋2×32＋3×33＋…＋n·3n①‎ ‎3＝1×32＋2×33＋3×34＋…＋(n－1)·3n＋n·3n+1②‎ ‎①－②得：－2＝31＋32＋33＋…＋3n－n·3n+1＝‎ 所以＝‎ 考点：等差数列的性质；数列求和.‎ ‎【方法点晴】本题主要考查了等差数列，等比数列的概念，属于高考中常考知识点，难度不大；常见的数列求和的方法有公式法即等差等比数列求和公式，分组求和类似于，其中和分别为特殊数列，裂项相消法类似于，错位相减法类似于，其中为等差数列，为等比数列等.‎ ‎3.（本小题满分12分）‎ 已知某企业的近3年的前7个月的月利润（单位：百万元）如下面的折线图所示：‎ ‎（1）试问这3年的前7个月中哪个月的月平均利润较高？‎ ‎（2）通过计算判断这3年的前7个月的总利润的发展趋势；‎ ‎（3）试以第3年的前4个月的数据（如下表），用线性回归的拟合模式估测第3年8月份的利润.‎ 相关公式：，. ‎ ‎【答案】（1）月和月的平均利润最高；（2）前个月的总利润呈上升趋势；（3）万元.‎ ‎（3）∵，，，‎ ‎∴，………………9分 ‎∴，………………10分 ‎∴，………………11分 当时，（百万元），∴估计月份的利润为万元.………………12分 考点：折线图；线性回归分析.‎ ‎4.（本小题满分12分）‎ 在直三棱柱中，分别是的中点.‎ ‎（1）证明: 平面平面；‎ ‎（2）证明: 平面；‎ ‎（3）设是的中点，求三棱锥的体积.‎ ‎【答案】（1）证明见解析；（2）证明见解析；（3）．‎ 试题解析：（1）在 中，‎ ‎,由已知，且, 可得平面, ‎ 又平面平面平面. ‎ ‎（2）取的中点，连接,在 中，, 而平面 直线平面, 在矩形中，分别是，的中点，，‎ 而平面，平面，‎ 平面平面，又平面，故平面.‎ ‎（3）取的中点,连接, 则, 且, ‎ 又平面平面是的中点 ‎ 所以.‎ 考点：直线与平面的位置关系的判定与证明；几何体的体积的计算.‎ ‎5.（本小题满分12分）‎ ‎ 如图，已知椭圆的中心在坐标原点，焦点在轴上，它的一个顶点为，且离心率等于，过点的直线与椭圆相交于不同两点，，点在线段上．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）设，若直线与轴不重合，试求的取值范围．‎ ‎【答案】（1）；（2）．‎ 试题解析：（1）设椭圆的标准方程是，‎ 由于椭圆的一个顶点是，故，根据离心率是得，‎ 解得，所以椭圆的标准方程为．‎ 考点：直线与圆锥曲线的综合问题．‎ ‎【方法点晴】本题主要考查了直线与圆锥曲线的位置关系的综合问题，其中解答中涉及到椭圆的标准方程求解，直线与圆锥曲线的位置关系的综合考查，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力，此类问题解答的关键在把直线方程和曲线方程联立，转化为根与系数的关系、韦达定理的应用是解答的关键，试题有一定的难度，属于中档试题．‎ ‎6．（本小题满分12分）‎ 已知函数，.‎ ‎（1）当时，求函数在上的单调区间；‎ ‎（2）若函数存在两个极值点，求的取值范围.‎ ‎【答案】（1）在上单调递减，在上单调递增；（2）.‎ ‎【解析】‎ 试题分析：（1）当时，，定义域为，求导得，故函数在上递减，在上递增；（2）令，，利用导数求得函数，由此可去掉绝对值，再对函数求导，对分成，，三类，讨论函数的极值情况，由此求得实数的取值范围.‎ ‎（2）令，，‎ 当时，；当时，.‎ 在上单调递增，在上单调递减，.‎ ‎，‎ ‎.‎ 当时，；，‎ 函数在上单调递减，在上单调递增，函数恰有一个极小值，不符合题意.‎ 当时，，或，‎ 函数在上单调递增，在上单调递减，在上单调递增，函数恰有一个极大值一个极小值，符合题意.‎ 当时，，函数在上单调递增，既无极大值也无极小值，不符合题意.‎ 当时，；或，‎ 函数在上单调递增，在上单调递减，在上单调递增，函数恰有一个极大值一个极小值，符合题意.‎ 综上所述，的取值范围是.‎ 考点：函数导数与不等式.‎ ‎【方法点晴】本题主要考查导数与不等式的知识，考查含有绝对值函数的处理方法.第一问由于参数值是知道的，函数的解析式知道，利用导数就可以求得函数的单调区间.第二问先处理绝对值里面的函数，方法是利用导数，求得其最大值大于零，由此去掉绝对值.对函数求导后，利用分类讨论的方法，可的取值范围.‎ ‎7.（本小题满分10分）选修4-4：坐标系与参数方程 ‎ 已知，直线的参数方程为（为参数），曲线的参数方程为（为参数）.‎ ‎（1）若在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，点的极坐标为，判断点与直线的位置关系；‎ ‎（2）设点是曲线上的一个动点，求点到直线的距离的最大值与最小值的和.‎ ‎【答案】（1）点不在直线上；（2）.‎ 试题解析：‎ ‎（1）把点的极坐标为化为直角坐标为，‎ 把直线的参数方程（为参数），化为直角坐标方程为，‎ 由于点的坐标不满足直线的方程，故点不在直线上．‎ ‎（2）∵点是曲线上的一个动点，曲线的参数方程为（为参数），‎ 把曲线的方程化为直角坐标方程为表示以为圆心、半径等于1的圆，‎ 圆心到直线的距离，‎ 故点到直线的距离的最小值为，最大值为，‎ ‎∴点到直线的距离的最大值与最小值的和为．‎ 考点：坐标系与参数方程．‎ ‎8. （本小题满分10分）选修4-5：不等式选讲 已知函数，不等式的解集为．‎ ‎（1）若不等式的解集为，求证：；‎ ‎（2）若，且，求证：．‎ ‎【答案】（1）证明见解析；（2）证明见解析.‎ ‎【解析】‎ 试题分析：（1）等价于，∴，解得；（2）因为，又∵，，∴，∴，进而可得结论.‎ 试题解析：证明：（1）由，即，可得，∴，解得，‎ ‎∴．‎ 同理可得，即，∴，‎ 故．‎