【数学】江西省都昌蔡岭慈济中学2020届高三下学期5月月考试题（文）

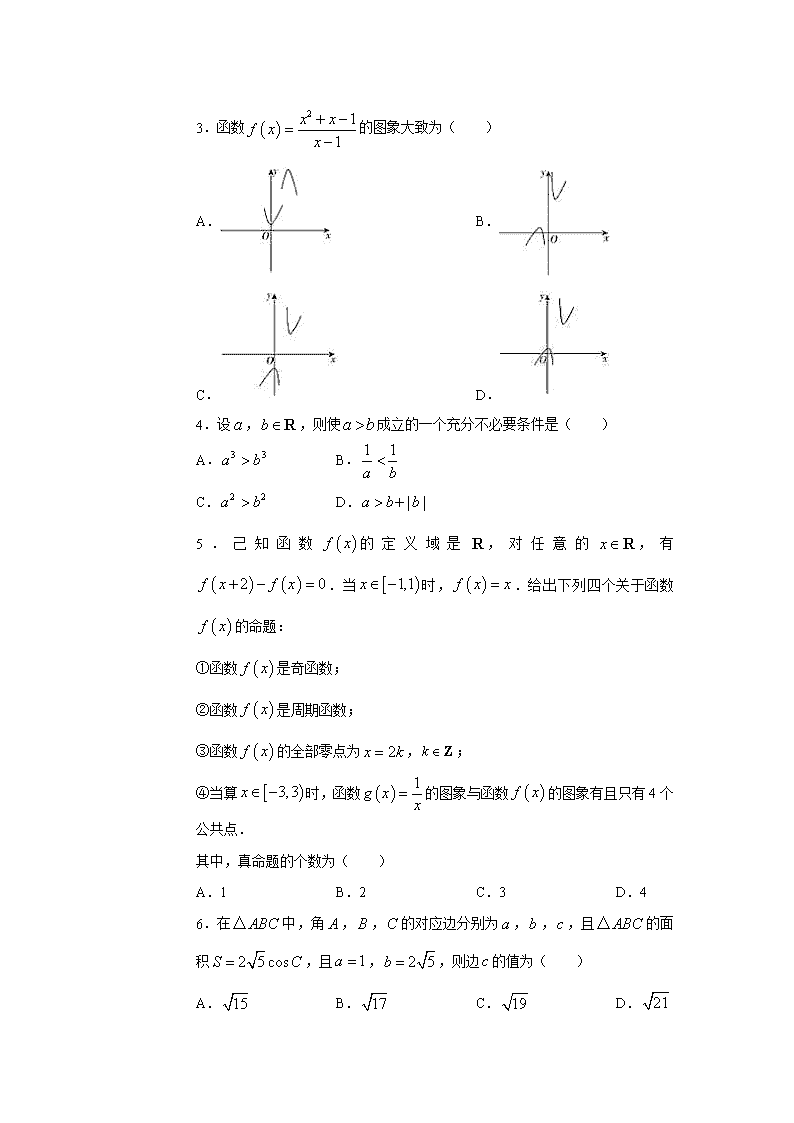
【数学】江西省都昌蔡岭慈济中学2020届高三下学期5月月考试题（文）

江西省都昌蔡岭慈济中学2020届 高三下学期5月月考 注意事项：‎ ‎1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。‎ ‎2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎4．考试结束后，请将本试题卷和答题卡一并上交。‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设全集是实数集，或，，则（ ）‎ A． B． ‎ C． D．‎ ‎2．以下说法错误的是（ ）‎ A．命题“若，则”的逆否命题为“若，‎ 则”‎ B．“”是“”的充分不必要条件 C．若命题存在，使得，则：对任意，‎ 都有 D．若且为假命题，则均为假命题 ‎3．函数的图象大致为（ ）‎ A． B．‎ C． D．‎ ‎4．设，，则使成立的一个充分不必要条件是（ ）‎ A． B． ‎ C． D．‎ ‎5．己知函数的定义域是，对任意的，有．当时，．给出下列四个关于函数的命题：‎ ‎①函数是奇函数；‎ ‎②函数是周期函数；‎ ‎③函数的全部零点为，；‎ ‎④当算时，函数的图象与函数的图象有且只有4个公共点．‎ 其中，真命题的个数为（ ）‎ A．1 B．2 C．3 D．4‎ ‎6．在中，角，，的对应边分别为，，，且的面积，且，，则边的值为（ ）‎ A． B． C． D．‎ ‎7．当时，，则下列大小关系正确的是（ ）‎ A． B．‎ C． D．‎ ‎8．已知，，，则实数，，的大小关系是（ ）‎ A． B． ‎ C． D．‎ ‎9．已知函数是定义域在上的偶函数，且，当时，，则关于的方程在上所有实数解之和为（ ）‎ A．1 B．3 C．6 D．7‎ ‎10．若，，则，的大小关系是（ ）‎ A． B．‎ C． D．，的大小由的取值确定 ‎11．条件“或”是条件“有极值点”成立的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎12．已知函数，若关于的不等式的解集为，且，，则实数的取值范围为（ ）‎ A． B． ‎ C． D．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分．‎ ‎13．已知全集为，集合，，则______．‎ ‎14．如果在某种细菌培养过程中，细菌每10 min分裂1次（1个分裂成2个），那么经过1 h，1个这种细菌可以分裂成________个．‎ ‎15．已知函数，集合，‎ 集合，‎ 若，则实数的取值范围是________．‎ ‎16．奇函数对任意实数都有成立，且时，，则______．‎ 三、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明 过程或演算步骤．‎ ‎17．（10分）已知函数且的图象恒过定点，二次函数的图象经过点，且的解集为．‎ ‎（1）求的解析式；‎ ‎（2）求函数，的最值．‎ ‎18．（12分）已知函数，是奇函数．‎ ‎（1）求实数m的值；‎ ‎（2）画出函数的图象，并根据图象求解下列问题．‎ ‎①写出函数的值域；‎ ‎②若函数在区间上单调递增，求实数a的取值范围．‎ ‎19．（12分）已知：函数，．‎ ‎（1）若的定义域为，求的取值范围；‎ ‎（2）设函数，若，对于任意总成立，求的取值范围．‎ ‎20．（12分）计算下列各式的值：‎ ‎（1）．‎ ‎（2）．‎ ‎21．（12分）已知函数，‎ 且满足．‎ ‎（1）求函数的定义域及a的值；‎ ‎（2）若关于x的方程有两个不同的实数解，求t的取值范围．‎ ‎22．（12分）投资商到一开发区投资72万元建起一座蔬菜加工厂，经营中，第一年支出12万元，以后每年支出增加4万元，从第一年起每年蔬菜销售收入50万元，设表示前n年的纯利润总和（前年总收入-前年的总支出-投资额72万元）‎ ‎（1）该厂从第几年开始盈利？‎ ‎（2）该厂第几年平均纯利润达到最大？并求出年平均纯利润的最大值．‎ 参考答案 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．【答案】C ‎【解析】由于或，所以，‎ ‎，所以．‎ ‎2．【答案】D ‎【解析】A选项：根据逆否命题的定义可知：原命题的逆否命题为“若，则”，可知A正确；‎ B选项：由，解得，因此“”是“”的充分不必要，‎ 可知B正确；‎ C选项：根据命题的否定可知对任意，都有，可知C正确；‎ D选项：由且为假命题，则至少有一个为假命题，因此D不正确，‎ 本题正确选项D．‎ ‎3．【答案】D ‎【解析】，‎ 故该图象是由函数的图象先向右平移个单位长度，再向上平移个单位长度得到的，‎ 由于函数在上单调递增，在上单调递减，在上单调递减，在上单调递增，‎ 故函数在上单调递增，在上单调递减，在上单调递减，在上单调递增．‎ ‎，故函数的图象大致为D项．‎ ‎4．【答案】D ‎【解析】对于A，根据函数的单调性可知，，是充要条件；‎ 对于B，时，可以得到，对应的结果为当时，；‎ 当时，，所以其为既不充分也不必要条件；‎ 对于C，由，可以得到，对于，的大小关系式不能确定的，‎ 所以是既不充分也不必要条件；‎ 故排除A，B，C，经分析，当时，得到，∴充分性成立，当时，不一定成立，如，但，必要性不成立，故选D．‎ ‎5．【答案】B ‎【解析】∵对任意的，有，∴对任意的，，‎ ‎∴是周期为2的函数，∴，‎ 又∵当时，，∴，∴函数不是奇函数，‎ 故①错误，②正确．‎ 当时，，∴，‎ 又∵是周期为2的函数，∴函数的全部零点为，，故③正确．‎ ‎∵当时，，令，解得（舍）或；‎ 当时，，‎ 令，则，解得或（舍）；‎ 当时，，‎ 令，则，解得或（舍），‎ ‎∴共有3个公共点，故④错误．‎ 因此真命题的个数为2个，故选B．‎ ‎6．【答案】B ‎【解析】由题意得，三角形的面积，‎ 所以，所以，‎ 由余弦定理得，所以．‎ ‎7．【答案】D ‎【解析】根据，得到，而，‎ 所以根据对数函数的单调性可知时，，‎ 从而可得，函数单调递增，所以，‎ 而，所以有，故选D．‎ ‎8．【答案】B ‎【解析】由题意，设，可得，，‎ 所以，根据零点的存在定理，可得，‎ 设，可得，，所以，‎ 根据零点的存在定理，可得，‎ 令，可得，‎ ‎，‎ 所以，可得，‎ 综上可得，故选B．‎ ‎9．【答案】D ‎【解析】因为，则，所以的最小正周期为，‎ 又由得的图像关于直线对称．‎ 令，则的图像如图所示，‎ 由图像可得，与的图像在有7个交点且实数解的和为，故选D．‎ ‎10．【答案】A ‎【解析】‎ ‎∵‎ 且，∴，‎ 又，∴．‎ ‎11．【答案】B ‎【解析】“有极值点”‎ 即“有两个不同的零点”，‎ ‎，得“或”“或”，‎ 但“或”推不出“或”，故选B．‎ ‎12．【答案】A ‎【解析】易知当，时，，‎ 的图象如图所示：‎ 当直线在图中的位置时，，得，‎ 为方程的两根，‎ 即的两根，故，‎ 而，‎ 则，‎ 即，解得，所以；‎ 当直线在图中的位置时，且，得，‎ 此时，则，得，‎ 所以，的取值范围是．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分．‎ ‎13．【答案】‎ ‎【解析】因为，‎ ‎，‎ 故可得，故答案为．‎ ‎14．【答案】64‎ ‎【解析】细菌每10 min分裂1次（1个分裂成2个），‎ 经过1 h可分裂6次，可分裂成（个），故答案为64．‎ ‎15．【答案】‎ ‎【解析】由题意，函数，则集合，‎ 又由，‎ 由，令，‎ 即，解得，，‎ 所以，‎ 要使得，则满足，解得，‎ 所以，所以实数的取值范围是，‎ 故答案为．‎ ‎16．【答案】‎ ‎【解析】，‎ 则，‎ 又，，‎ 则，故答案为．‎ 三、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤．‎ ‎17．【答案】（1）；（2）时，；时，．‎ ‎【解析】（1）∵且的图象恒过定点，‎ 由题意可设，，‎ ‎∵的图象过点，∴，∴，‎ ‎∴．‎ ‎（2）令，‎ ‎∵，∴，则，，‎ ‎∵在上是增函数，‎ ‎∴当，即时，；‎ 当，即时，．‎ ‎18．【答案】（1）；（2）①；②．‎ ‎【解析】（1）因为是奇函数，所以，‎ 即，解得．‎ 又易检验知：当时，是奇函数，故所求实数m的值为2．‎ ‎（2）由（1）得，‎ 如图，画出函数的图象：‎ ‎①由图知，函数的值域为．‎ ‎②由图知，函数的单调递增区间为，‎ 所以根据函数在区间上单调递增，‎ 可知需满足，解得．‎ 故所求实数m的取值范围为．‎ ‎19．【答案】（1）；（2）．‎ ‎【解析】（1）函数的定义域为，即在上恒成立，‎ 当时，恒成立，符合题意；‎ 当时，必有，‎ 综上：的取值范围是．‎ ‎（2），‎ ‎，对任意总成立，‎ 等价于在总成立，‎ 即在上恒成立，‎ 设，因为，所以，‎ 不等式组化为，‎ 时，（当且仅当时取等号），‎ 时，不等式组显然成立，‎ 当时，恒成立，‎ ‎，即，‎ 在上递减，所以的最小值为，，‎ 综上所述，的取值范围是．‎ ‎20．【答案】（1）（或写成）；（2）3．‎ ‎【解析】（1）原式 ‎（或写成）．‎ ‎（2）原式．‎ ‎21．【答案】（1）定义域为，；（2）．‎ ‎【解析】（1）由，解得，‎ 所以函数的定义域为．‎ 因为，所以，‎ 所以，‎ 又，故化简得所求．‎ ‎（2）由（1）可知，其中，‎ 所以由题设得关于x的方程在内有两个不同的实数解．（*）‎ 设函数，‎ 则因为该函数图像的对称轴方程为，‎ 所以结合（*）知只需，解得，‎ 故所求实数t的取值范围是．‎ ‎22．【答案】（1）从第3年开始盈利；（2）第6年，投资商平均年平均纯利润最大，最大值为16万元．‎ ‎【解析】（1）依题意前年总收入-前年的总支出投资额72万元，‎ 可得，‎ 由，得，解得，‎ 由于，所以从第3年开始盈利．‎ ‎（2）年平均利润，‎ 当且仅当，即时等号成立，‎ 即第6年，投资商平均年平均纯利润最大，最大值为16万元．‎