数学理卷·2018届北京市朝阳区高三上学期期中考试试题(解析版)
北京市朝阳区2017-2018学年度第一学期高三年级期中统一考试
数学试卷(理工类)
(考试时间120分钟 满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.
1. 已知集合A={x|x>1},B={x|log2x>1},则A∩B=
A. {x|x>1} B. {x|1
2} D. {x|x>0}
【答案】C
【解析】集合A={x|x>1},B={x|log2x>1}={x|x>2},
所以A∩B={x|x>2}.
故选C.
2. 已知实数x,y满足条件 则x+2y的最大值为
A. 12 B. 10
C. 8 D. 6
【答案】B
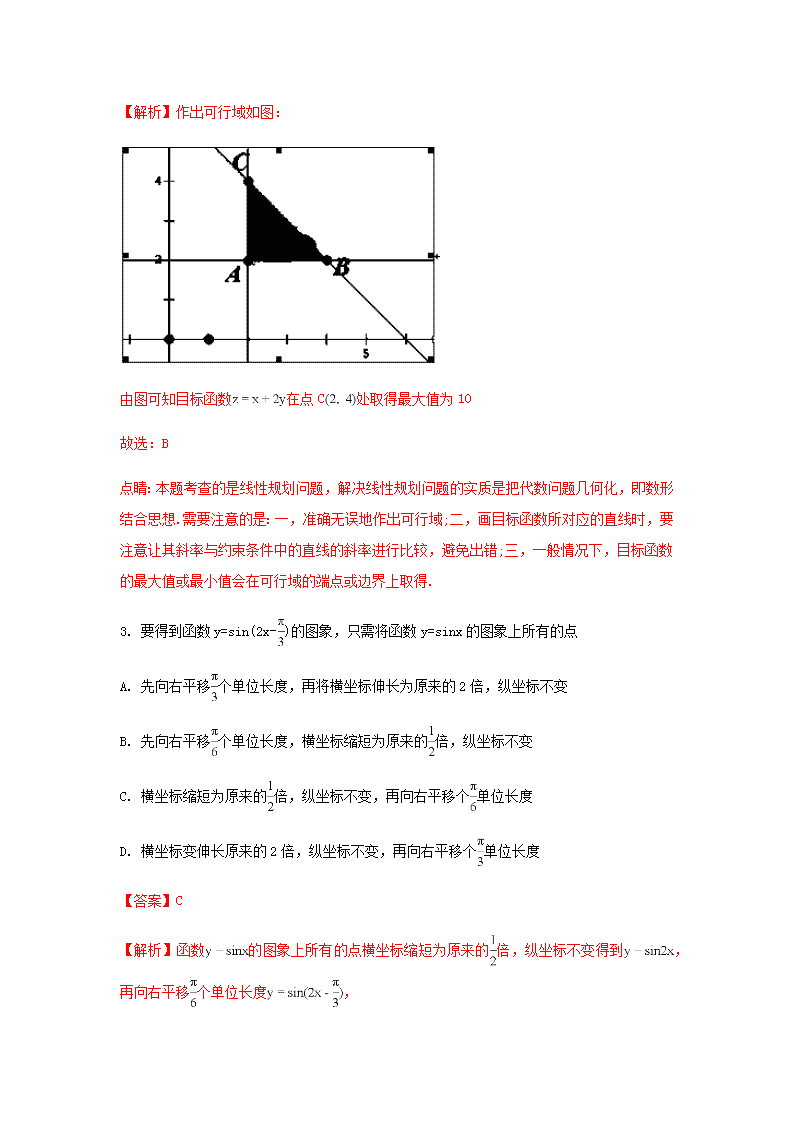
【解析】作出可行域如图:
由图可知目标函数在点C处取得最大值为10
故选:B
点睛:本题考查的是线性规划问题,解决线性规划问题的实质是把代数问题几何化,即数形结合思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意让其斜率与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大值或最小值会在可行域的端点或边界上取得.
3. 要得到函数y=sin(2x-)的图象,只需将函数y=sinx的图象上所有的点
A. 先向右平移个单位长度,再将横坐标伸长为原来的2倍,纵坐标不变
B. 先向右平移个单位长度,横坐标缩短为原来的倍,纵坐标不变
C. 横坐标缩短为原来的倍,纵坐标不变,再向右平移个单位长度
D. 横坐标变伸长原来的2倍,纵坐标不变,再向右平移个单位长度
【答案】C
【解析】函数的图象上所有的点横坐标缩短为原来的倍,纵坐标不变得到,再向右平移个单位长度,
故选:C
4. 已知非零平面向量,,则“|+|=||+||”是“存在非零实数l,使=λ”的
A. 充分而不必要条件
B. 必要而不充分条件
C. 充分必要条件
D. 既不充分也不必要条件
【答案】A
【解析】(1)若|+|=||+||,则,方向相同,
∴,共线,∴存在非零实数λ,使=λ.
∴“|+|=||+||”是“存在非零实数λ,使=λ”的充分条件;
(2)若存在非零实数λ,使=λ,则,共线,
∴当,方向相同时,| +|=||+||,
当,方向相反时,| +|<||+||,
∴∴“|+|=||+||”不是“存在非零实数λ,使=λ”的必要条件。全品教学网...全品教学网...全品教学网...全品教学网...全品教学网...全品教学网...全品教学网...
故选A.
5. 已知Sn是等差数列{an}(n∈N*)的前n项和,且S5>S6>S4,以下有四个命题:
①数列{Sn}中的最大项为S10
②数列{an}的公差d<0
③S10>0
④S11<0
其中正确的序号是
A. ②③ B. ②③④
C. ②④ D. ①③④
【答案】B
【解析】Sn是等差数列{an}(n∈N*)的前n项和,由,得,
所以公差d=,②正确;
由知,数列{Sn}中的最大项为S5,①不正确;
,③正确;
,④正确.
故选B.
6. 如图,在直角梯形ABCD中,AB//CD,AD⊥DC,E是CD的中点DC=1,AB=2,则·=
A. 5 B. -5
C. 1 D. -1
【答案】D
【解析】
过E作EF⊥AB,垂足为F,
则,
∴·.
故选D.
点睛:平面向量数量积的类型及求法
(1)求平面向量数量积有三种方法:一是夹角公式a·b=|a||b|cos θ;二是坐标公式a·b=x1x2+y1y2;三是利用数量积的几何意义.
(2)求较复杂的平面向量数量积的运算时,可先利用平面向量数量积的运算律或相关公式进行化简.
7. 袋子里有编号为2,3,4,5,6的五个球,某位教师从袋中任取两个不同的球.教师把所取两球编号的和只告诉甲,其乘积只告诉乙,再让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲说:“我现在可以确定两个球的编号了.”
根据以上信息,你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球
C. 可能有5号球 D. 可能有6号球
【答案】D
【解析】甲说:“我无法确定.”说明两球编号的和可能为7包含(2,5),(3,4),可能为8包含(2,6),(3,5),可能为9包含(3,6),(2,7)
乙说:“我无法确定.”说明两球编号的乘积为12包含(3,4)或(2 ,6)
根据以上信息,可以推断出抽取的两球中可能有6号球
故选:D
点睛:本题是一道通俗易懂的合情推理题目,主要考查同学们的逻辑思维能力和推理能力,问题难度不大,认真审题是关键.
8. 已知函数f(x)=sin(cosx)-x与函数g(x)=cos(sinx)-x在区间(0,)都为减函数,设x1,x2,x3∈(0,),且cosx1=x1,sin(cosx2)=x2,cos(sinx3)=x3,则x1,x2,x3的大小关系是( )
A. x10,解得:,
令v′(r)<0,解得:,
故v(r)在(0,)递增,在(,)递减,
故当r=时V最大,
故答案为:.
13. 将集合M={1,2,3,...,15}表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为________;请写出满足上述条件的集合M的5个三元子集__________(只写出一组)
【答案】 (1). 24 (2). {1,8,15},{3,7,14},{5,6,13},{2,10,12},{4,9,11}(答案不唯一)
【解析】因为5个三元子集(三元集:含三个元素的集合)的并集为集合M={1,2,3,...,15}
所以元素总和为:,
又因为这5个三元子集的元素之和都相等,所以每个集合的元素和为.
满足上述条件的集合M的5个三元子集可以是:{1,8,15},{3,7,14},{5,6,13},{2,10,12},{4,9,11}(答案不唯一).
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
14. 已知数列{an}的前n项和为Sn,满足Sn=2an-1.(n∈N*)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=an,求数列{bn}的前n项和Tn.
【答案】(Ⅰ)an=2n-1;(Ⅱ)Tn=.
【解析】试题分析:(Ⅰ)由n≥2时,an=Sn-Sn-1即可得通项公式;
(Ⅱ)bn=an=2n-1=1-n,利用等差数列求和公式求解即可.
试题解析:
(Ⅰ)当n=1时,a1=1.
当n≥2时,an=Sn-Sn-1,
an=2an-2an-1,即an=2an-1
所以数列{an}是首项为1,公比为2的等比数列.
故an=2n-1,n∈N*.
(Ⅱ)由已知得bn=an=2n-1=1-n.
因为bn-bn-1=(1-n)-(2-n)=-1,
所以{bn}是首项为0,公差为-1的等差数列.
故{bn}的前n项和Tn=.
15. 已知函数f(x)=2sinxcos(x-).
(Ⅰ)求函数f(x)的最小正周期.
(Ⅱ)当x∈[0,]时,求函数f(x)的取值范围.
【答案】(Ⅰ);(Ⅱ)f(x)∈[0,1+].
【解析】试题分析:(Ⅰ)由两角差的余弦公式展开,结合二倍角公式化简得f(x)=sin(2x-
)+,进而得周期;
(Ⅱ)由x∈[0,]得2x-∈[-,],即可得sin(2x-)∈[-,1],从而得解.
试题解析:
因为f(x)=2sinx×cos(x-),
所以f(x)=2sinx×(cosxcos+sinxsin)=sinx×cosx+sin2x=sin2x+(1-cos2x)=sin(2x-)+.
(Ⅰ)函数f(x)的最小正周期为.
(Ⅱ)因为x∈[0,],所以2x-∈[-,].
所以sin(2x-)∈[-,1].
所以f(x)∈[0,1+].
16. 在△ABC中,A=,=.
(Ⅰ)试求tanC的值;
(Ⅱ)若a=5,试求△ABC的面积.
【答案】(Ⅰ)tanC=;(Ⅱ).
【解析】试题分析:(Ⅰ)由正弦定理得:,将A=代入求解得4sinC=3cosC,进而得tanC的值;
(Ⅱ)结合条件由余弦定理a2=b2+c2-2bccosA得25=b2+(b)2-2b×b×.求解b,c代入S=bcsinA求解面积即可.
试题解析:
(Ⅰ)因为A=,=,所以==.
所以7sinC=3
所以7sinC=3
所以7sinC=3cosC+3sinC.
所以4sinC=3cosC.
所以tanC=.
(Ⅱ)因为A=,=,a=5,由余弦定理a2=b2+c2-2bccosA得25=b2+(b)2-2b×b×.
所以b=7,c=3.
所以△ABC的面积S=bcsinA=×7×3×.
17. 已知函数f(x)=(x2-ax+a)e-x,a∈R
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(x)=f’(x),其中f’(x)为函数f(x)的导函数.判断g(x)在定义域内是否为单调函数,并说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)函数求导得f’(x)=-(x-2)(x-a)e-x,讨论a和2的大小,结合导数的正负讨论单调性即可;
(Ⅱ)g’(x)=f"(x)=[x2-(a+4)x+3a+2]×e-x,记h(x)=x2
-(a+4)x+3a+2,通过二次函数的性质知函数有正有负,从而得g(x)在定义域内不为单调函数.
试题解析:
(Ⅰ)函数f(x)的定义域为{x|x∈R}..
①当a<2时,令f’(x)<0,解得:x2,f(x)为减函数;
令f’(x)>0,解得:a2时,令f’(x)<0,解得:x<2或x>a,函数f(x)为减函数;
令f’(x)>0,解得:22时,f(x)的单调递减区间为(-∞,2),(a,+∞);单调递增区间为(2,a).
(Ⅱ)g(x)在定义域内不为单调函数,以下说明:
g’(x)=f"(x)=[x2-(a+4)x+3a+2]×e-x.
记h(x)=x2-(a+4)x+3a+2,则函数h(x)为开口向上的二次函数.
方程h(x)=0的判别式△=a2-4a+8=(a-2)2+4>0恒成立.
所以,h(x)有正有负,从而g’(x)有正有负
故g(x)在定义域内不为单调函数.
18. 已知函数f(x)=-lnx-.
(Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求证:lnx≥-
(Ⅲ)判断曲线y=f(x)是否位于x轴下方,并说明理由.
【答案】(Ⅰ)(-1)x-y-+1=0;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(Ⅰ)函数求导得切线斜率为f’(1)=-1,再利用直线的点斜式求解即可;
(Ⅱ)要证明lnx≥-,(x>0)”等价于“xlnx≥-”,设函数g(x)=xlnx,求导结合单调性得g()即可证得;
(Ⅲ)由(Ⅱ)可知lnx≥,所以f(x)≤-(),求导结合单调性得k(x)≤k(1)=0恒成立,即可证得.
试题解析:
函数的定义域为(0,+∞),
f’(x)=--+
(Ⅰ)f’(1)=-1,又f(1)=-
曲线y=f(x)在x=1处的切线方程为
y+=(-1)x-+1.
即(-1)x-y-+1=0.
(Ⅱ)“要证明lnx≥-,(x>0)”等价于“xlnx≥
设函数g(x)=xlnx.
令g’(x)=1+lnx=0,解得.
x
(0,)
()
g(x)
-
0
+
g(x)
递减
递增
因此,函数g(x)的最小值为g()=-,故xlnx≥.
即lnx≥.
(Ⅲ)曲线y=f(x)位于x轴下方.理由如下:
由(Ⅱ)可知lnx≥,所以f(x)≤-=().
设k(x)=,则k’(x)=
令k’(x)>0得01.
所以k(x)在(0,1)上为增函数,(1,+∞)上为减函数.
所以当x>0时,k(x)≤k(1)=0恒成立,当且仅当x=1时,k(1)=0.
又因为f(1)=-<0,所以f(x)<0恒成立.
故曲线y=f(x)位于x轴下方.
点睛:利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.
19. 数列a1,a2……an是正整数1,2,……,n的任一排列,且同时满足以下两个条件:
①a1=1;②当n≥2时,|ai-ai+1|≤2(i=1,2,…,n-1).
记这样的数列个数为f(n).
(I)写出f(2),f(3),f(4)的值;
(II)证明f(2018)不能被4整除.
【答案】(Ⅰ)f(2)=1,f(3)=2,f(4)=4;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)根据题意,由f(n)的定义,计算即可得答案;
(Ⅱ)根据题意,把满足条件①②的数列称为n项的首项最小数列,对于n个数的首项最小数列,由于a1=1,故a2=2或3;分析可得递推关系为f(n)=f(n-1)+f(n-3)+1,进而求出f(2),f(3),…,f(2018)各数被4除的余数,分析可得它们构成14为周期的数列,即可得结论.
试题解析:
(Ⅰ)解:(Ⅰ)根据题意,①a1=1;②当n⩾2时, |ai-ai+1|≤2(i=1,2,…,n−1);
则f(2)=1,f(3)=2,f(4)=4.
(Ⅱ)证明:把满足条件①②的数列称为n项的首项最小数列.
对于n个数的首项最小数列,由于a1=1,故a2=2或3.
(1)若a2=2,则a2-1,a3-1,,an-1构成n-1项的首项最小数列,其个数为f(n-1);
(2)若a2=3,a3=2,则必有a4=4,故a4-3,a5-3,……,an-3构成n-3项的首项最小数列,其个数为f(n-3);
(3)若a2=3,则a3=4或a3=5.设ak+1是这数列中第一个出现的偶数,则前k项应该是1,3,,2k-1,ak+1是2k或2k-2,即ak与ak+1是相邻整数.
由条件②,这数列在ak+1后的各项要么都小于它,要么都大于它,因为2在ak+1之后,故ak+1后的各项都小于它.
这种情况的数列只有一个,即先排递增的奇数,后排递减的偶数.
综上,有递推关系:f(n)=f(n-1)+f(n-3)+1,n≥5.
由此递推关系和(I)可得,f(2),f(3),,f(2018)各数被4除的余数依次为:
1,1,2,0,2,1,2,1,3,2,0,0,3,0,1,1,2,0,…
它们构成14为周期的数列,又2018=14144+2,
所以f(2018)被4除的余数与f(2)被4除的余数相同,都是1,
故f(2018)不能被4整除.