- 2021-06-20 发布 |
- 37.5 KB |
- 9页


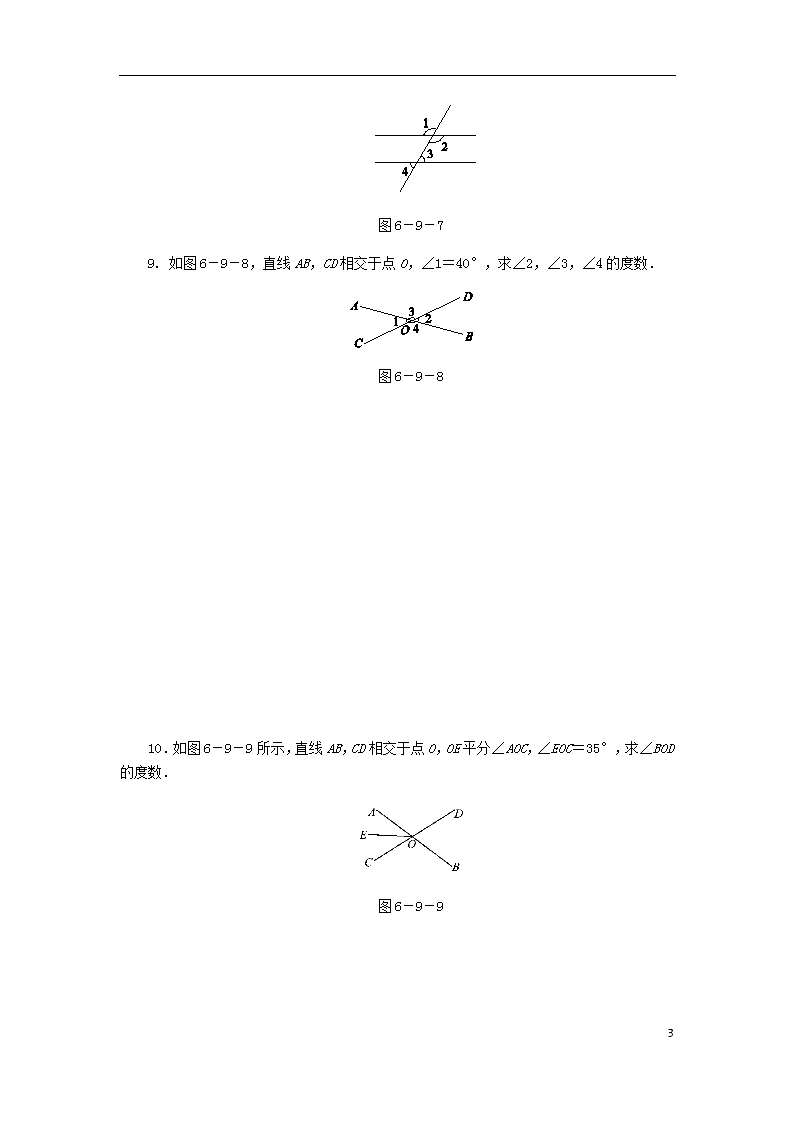
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019七年级数学上册 第6章 图形的初步知识 6直线的相交
6.9 直线的相交 第1课时 对顶角 知识点1 对顶角的意义 1.下列图形中,∠1与∠2是对顶角的是( ) 图6-9-1 2.如图6-9-2所示,BE,CF相交于点O,OA,OD是射线,其中构成对顶角的角是____________. 图6-9-2 知识点2 对顶角的性质 3.如图6-9-3,直线a,b相交于点O,∠1+∠3=________,∠2+∠3=________(邻补角的定义),所以∠1________∠2(同角的补角相等).由此可知对顶角________. 9 图6-9-3 4.已知∠α和∠β是对顶角,∠α=30°,则∠β的度数为( ) A.30° B.60° C.70° D.150° 5.如图6-9-4,图中是对顶角量角器,用它测量角的原理是______________. 图6-9-4 6.如图6-9-5,直线AB,CD,EF交于一点O. 图6-9-5 (1)∠EOB的对顶角是________; (2)________是∠AOE的对顶角; (3)若∠AOC=76°,则∠BOD的度数为________. 7.如图6-9-6所示,直线AB与CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC=________°. 图6-9-6 8.如图6-9-7所示,∠1=120°,∠2+∠3=180°,则∠4=________°. 9 图6-9-7 9. 如图6-9-8,直线AB,CD相交于点O,∠1=40°,求∠2,∠3,∠4的度数. 图6-9-8 10.如图6-9-9所示,直线AB,CD相交于点O,OE平分∠AOC,∠EOC=35°,求∠BOD的度数. 图6-9-9 9 11.如图6-9-10,直线AB,CD,EF相交于点O,∠AOD=150°,∠EOD=80°,求∠AOF的度数. 图6-9-10 12.如图6-9-11,直线AB,CD相交于点O,OE平分∠AOC,OF平分∠DOB,则点E,O,F在同一直线上,请说明理由.(补全解答过程) 9 图6-9-11 解:∵直线AB,CD相交于点O, ∴∠AOC=________(对顶角相等). ∵OE平分∠AOC,OF平分∠DOB, ∴∠AOE=______∠AOC,∠BOF=______∠DOB, ∴∠AOE=________. ∵∠AOF+∠BOF=∠AOB=180°, ∴∠AOF+∠AOE=∠EOF=180°, ∴点E,O,F在同一直线上. 13.如图6-9-12,直线AB与CD相交于点O,∠BOE=∠COF=90°,且∠BOF=32°,求∠AOC与∠EOD的度数. 图6-9-12 14.已知:如图6-9-13所示,直线AB,CD,EF相交于点O,∠1∶∠3=3∶1,∠2 9 =30°,求∠BOE的度数. 图6-9-13 15.观察图6-9-14,回答下列各题. (1)图①中,共有________对对顶角,可以看作________=________×________; (2)图②中,共有________对对顶角,可以看作________=________×________; (3)图③中,共有________对对顶角,可以看作________=________×________; (4)通过(1)~(3)各题中直线条数与对顶角对数之间的关系,若有n(n≥2)条直线相交于一点,则可形成几对对顶角? 图6-9-14 9 9 1.C 2.∠EOF和∠BOC,∠COE和∠BOF 3.180° 180° = 相等 4.A 5.对顶角相等 6.(1)∠AOF (2)∠BOF (3)76° 7.135 8.60 9.解:∵∠1=40°,∠1=∠2,∴∠2=40°. ∵∠1=40°,∠1+∠3=180°,∴∠3=140°. 又∵∠3=∠4,∴∠4=140°. 10. 解:∵OE平分∠AOC,∠EOC=35°, ∴∠AOC=2∠EOC=35°×2=70°. 由对顶角相等可知:∠BOD=∠AOC=70°. 11.解:∵∠AOD=150°,∠AOD+∠BOD=180°, ∴∠BOD=30°. 又∵∠EOD=80°,∴∠EOB=80°-30°=50°, ∴∠AOF=∠EOB=50°. 12.∠DOB ∠BOF 13. 解:∵∠COF=90°,∠BOF=32°, ∴∠COB=90°-32°=58°=∠AOD. ∵∠BOE=90°, ∴∠EOA=180°-90°=90°, ∠EOC=90°-∠COB=32°, ∴∠AOC=∠EOA+∠EOC=122°, 9 ∠EOD=∠EOA+∠AOD=148°. 14.解:∵∠1+∠2+∠3=180°, 且∠1∶∠3=3∶1,∠2=30°, ∴∠1=112.5°,∠3=37.5°, ∴∠BOE=∠1=112.5°. 15.解:(1)共有2对对顶角,可以看作2=2×1. (2)单个角是对顶角的有3对,两个角组成复合角的对顶角有3对,共有6对,可以看作6=3×2. (3)单个角是对顶角的有4对,两个角组成复合角的对顶角有4对,三个角组成复合角的对顶角有4对,共有12对,可以看作12=4×3. (4)n(n≥2)条直线相交于一点,可形成n(n-1)对对顶角. 9查看更多