2012年黄冈高考物理总复习决战资料

2012年黄冈高考物理总复习决战资料

2012 年黄冈高考物理总复习决战资料（绝密） 专题一 运动和力 【知识结构】 【典型例题】 例 1、如图 1—1 所示，质量为 m=5kg 的物体，置于一倾角为 30°的粗糙斜面体上，用一平行于斜面的大小为 30N 的力 F 推物体，使物体沿斜面向上匀速运动，斜面体质量 M=10kg，始终静止，取 g=10m/s2，求地面对斜面体的摩擦力及支持力． 物体受力情况 合力 为零 静止或匀速 直线运动状态 方法 三力平衡用 矢量三角形 对多体问题，整 体分析与隔离分 析交替使用 多力平衡用 正方分解法 恒 力 匀变速 运动 恒力与初 速度在一 条直线上 匀变速 直线运 动 力和运动状态变化 F=ma 已知力求运 解决两类问 已知运动求 恒力与初速度不 在一条直线上 匀变速曲线运 特例 平抛运动 0 2 0 0 22 0 2 1 2 2 2 t t t tt vvat s vt at vvs vt t vv as svvt = + =+ +== −= == 匀变速直 线运动的 规律 力的大小不 变 而方向变化 力的方向总 与速度垂直 匀速圆周运动 合力提供 向心力 带电粒子在 磁 天体的运 动 力的方向作周期性 作周期性加 速、 图像法解 答 振动的周期性导致波的周期性 振动的多解性与波的多解性是一致的 振动在媒质中 的 合力与位移 正比方向 简谐 运动 轨迹是圆 此类问题往往应用能量守恒定律和牛顿第二定 轨迹不是圆周的曲线 此类问题往往应用动能定理或守恒 合力的大小 和 方向均在变 黄冈中学：郑帆 例 2 、如图 1—3 所示，声源 S 和观察者 A 都沿 x 轴正方向运动，相对于地面的速率分别为 vS 和 vA，空气中声音传播 的速率为 Pv ，设 ,SPAPvvvv<<，空气相对于地面没有流动． （1）若声源相继发出两个声信号，时间间隔为△t，请根据发出的这两个声信号从声源传播到观察者的过程，确定观察 者接收到这两个声信号的时间间隔△t′． （2）利用（1）的结果，推导此情形下观察者接收到的声源频率与声源发出的声波频率间的关系式． 例 3、假设有两个天体，质量分别为 m1 和 m2，它们相距 r；其他天体离它们很远，可以认为这两个天体除相互吸引作 用外，不受其他外力作用．这两个天体之所以能保持距离．．．．．．．．．．．．．r．不变，完全是由于它们绕着共同“中心”（质心）做匀速圆周运．．．．．．．．．．．．．．．．．．．．．．．．．．．． 动，它们之间的万有引力作为做圆周运动的向心力．．．．．．．．．．．．．．．．．．．．．．，“中心”O 位于两个天体的连线上，与两个天体的距离分别为 r1 和 r2． （1）r1、r2 各多大？ （2）两天体绕质心 O 转动的角速度、线速度、周期各多大？ 例 4、A、B 两个小球由柔软的细线相连，线长 l=6m；将 A、B 球先后以相同的初速度 v0=4.5m/s，从同一点水平抛出 （先 A、后 B）相隔时间△t =0.8s． （1）A 球抛出后经多少时间，细线刚好被拉直？ （2）细线刚被拉直时，A、B 球的水平位移（相对于抛出点）各多大？（取 g=10m/s2） 例 5、内壁光滑的环形细圆管，位于竖直平面内，环的半径为 R（比细管的半径大得多）．在细圆管中有两个直径略小 F m M 图 1—1 vS vA S A x 图 1—3 于细圆管管径的小球（可视为质点）A 和 B，质量分别为 m1 和 m2，它们沿环形圆管（在竖直平面内）顺时针方向运动，经 过最低点时的速度都是 v0；设 A 球通过最低点时 B 球恰好通过最高点，此时两球作用于环形圆管的合力为零，那么 m1、m2、 R 和 v0 应满足的关系式是____________． 例 6、有两架走时准确的摆钟，一架放在地面上，另一架放入探空火箭中．假若火箭以加速度 a=8g 竖直向上发射，在 升高时 h=64km 时，发动机熄火而停止工作．试分析计算：火箭上升到最高点时，两架摆钟的读数差是多少？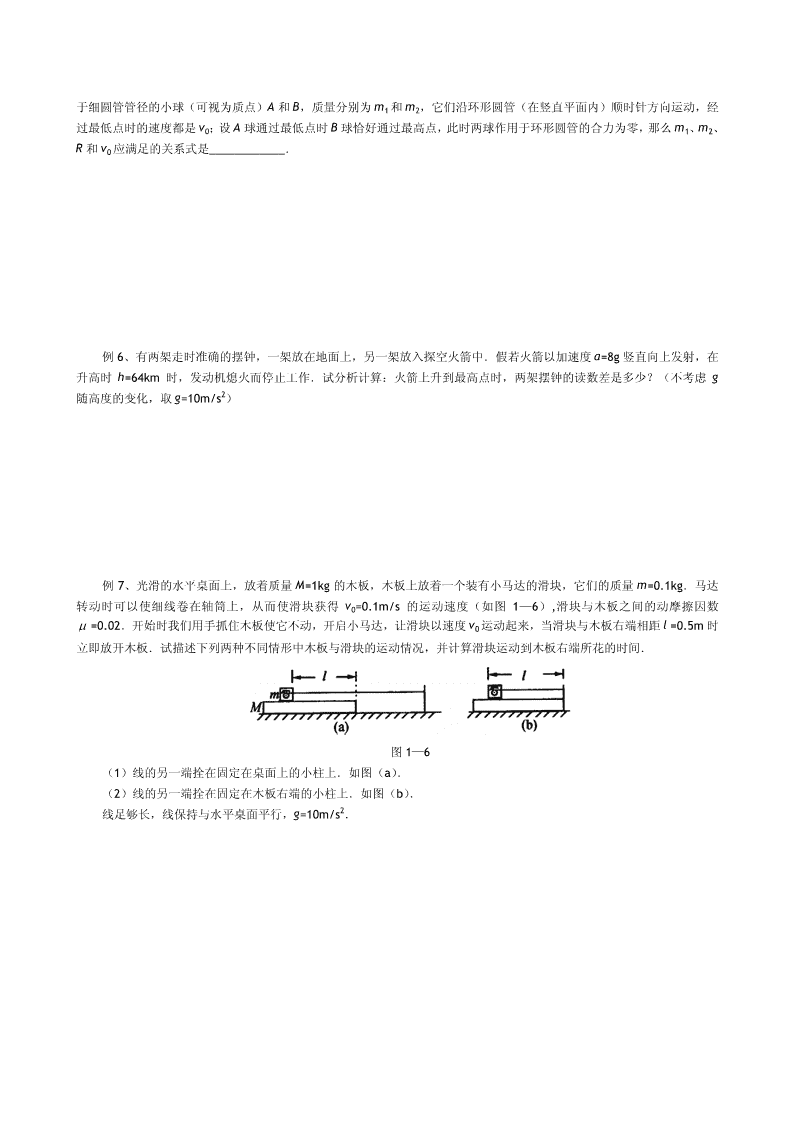（不考虑 g 随高度的变化，取 g=10m/s2） 例 7、光滑的水平桌面上，放着质量 M=1kg 的木板，木板上放着一个装有小马达的滑块，它们的质量 m=0.1kg．马达 转动时可以使细线卷在轴筒上，从而使滑块获得 v0=0.1m/s 的运动速度（如图 1—6）,滑块与木板之间的动摩擦因数 μ =0.02．开始时我们用手抓住木板使它不动，开启小马达，让滑块以速度 v0 运动起来，当滑块与木板右端相距 l =0.5m 时 立即放开木板．试描述下列两种不同情形中木板与滑块的运动情况，并计算滑块运动到木板右端所花的时间． 图 1—6 （1）线的另一端拴在固定在桌面上的小柱上．如图（a）． （2）线的另一端拴在固定在木板右端的小柱上．如图（b）． 线足够长，线保持与水平桌面平行，g=10m/s2． 例 8、相隔一定距离的 A、B 两球，质量相等，假定它们之间存在着恒定的斥力作用．原来两球被按住，处在静止状态．现 突然松开，同时给 A 球以初速度 v0，使之沿两球连线射向 B 球，B 球初速度为零．若两球间的距离从最小值（两球未接触） 在刚恢复到原始值所经历的时间为 t0，求 B 球在斥力作用下的加速度． （本题是 2000 年春季招生，北京、安徽地区试卷第 24 题） 【跟踪练习】 1、如图 1—7 所示，A、B 两球完全相同，质量为 m，用两根等长的细线悬挂在 O 点，两球之间夹着一根劲度系数为 k 的轻弹簧，静止不动时，弹簧位于水平方向，两根细线 之间的夹角为θ ．则弹簧的长度被压 缩了（ ） A． tanmg k θ B． 2tanmg k θ C． (tan )2mg k θ D． 2tan()2mg k θ 2、如图 1—8 所示，半径为 R、圆心为 O 的大圆环 固定在竖直平面内，两个轻质小圆环 套在大圆环上，一根轻质长绳穿过两个小圆环，它的两端都系上质量为 m 的重物，忽略小圆环的大小． （1）将两个小圆环固定在大圆环竖直对称轴的两侧θ =30°的位置上（如图），在两个小圆环间绳子的中点 C 处，挂上 一个质量 2M m= 的重物，使两个小圆环间的绳子水平，然后无初速释放重物 M，设绳子与大、小圆环间的摩擦均可忽略， 求重物 M 下降的最大距离． （2）若不挂重物 M，小圆环可以在大圆环上自由移动，且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略， 问两个小圆环分别在哪些位置时，系统可处于平衡状态？ 图 1—7 图 1—8 3、图 1—9 中的 A 是在高速公路上用超声测速仪测量车速的示意图，测速仪发出并接收超声波脉冲信号．根据发出和 接收到的信号间的时间差，测出被测物体的速度，图 B 中 P1、P2 是测速仪发出的超声波信号，n1、n2 分别是 P1、P2 由汽车 反射回来的信号，设测速仪匀速扫描，P1、P2 之间的时间间隔△t=1.0s，超声波在空气中传播的速度 v=340m/s，若汽车是 匀速行驶的，则根据图中可知，汽车在接收到 P1、P2 两个信号之间的时间内前进的距离是_________m，汽车的速度是 ________m/s． 图 1—9 4、利用超声波遇到物体发生反射，可测定物体运动的有关参量，图 1—10（a）中仪器 A 和 B 通过电缆线连接，B 为超 声波发射与接收一体化装置，仪器 A 和 B 提供超声波信号源而且能将 B 接收到的超声波信号进行处理并在屏幕上显示其波 形． 现固定装置 B，并将它对准匀速行驶的小车 C，使其每隔固定时间 T0 发射一短促的超声波脉冲，如图 1—10（b）中幅 度较大的波形，反射波滞后的时间已在图中标出，其中 T 和△T 为已知量，另外还知道该测定条件下超声波在空气中的速度 为 v0，根据所给信息求小车的运动方向和速度大小． 图 1—10 5、关于绕地球匀速圆周运动的人造地球卫星，下列说法中，正确的是（ ） A．卫星的轨道面肯定通过地心 B．卫星的运动速度肯定大于第一宇宙速度 C．卫星的轨道半径越大、周期越大、速度越小 D．任何卫星的轨道半径的三次方跟周期的平方比都相等 6、某人造地球卫星质量为 m，其绕地球运动的轨道为椭圆．已知它在近地点时距离地面高度为 h1，速率为 v1，加速度 为 a1，在远地点时距离地面高度为 h2，速率为 v2，设地球半径为 R，则该卫星． （1）由近地点到远地点过程中地球对它的万有引力所做的功是多少？ （2）在远地点运动的加速度 a2 多大？ A B (a) 7、从倾角为θ 的斜面上的 A 点，以水平初速度 v0 抛出一个小球．问： （1）抛出后小球到斜面的最大（垂直）距离多大？ （2）小球落在斜面上 B 点与 A 点相距多远？ 8、滑雪者从 A 点由静止沿斜面滑下，经一平台后水平飞离 B 点，地面上紧靠平台有一个水平台阶，空间几何尺度如图 1—12 所示．斜面、平台与滑雪板之间的动摩擦因数为 μ ，假设滑雪者由斜面底端进入平台后立即沿水平方向运动，且速 度大小不变．求： （1）滑雪者离开 B 点时的速度大小； （2）滑雪者从 B 点开始做平抛运动的水平距离． 9、如图 1—13 所示，悬挂在小车支架上的摆长为 l 的摆，小车与摆球一起以速度 v0 匀速向右运动．小车与矮墙相碰后 立即停止（不弹回），则下列关于摆球上升能够达到的最大高度 H 的说法中，正确的是（ ） A．若 0 2vgl= ，则 H=l B．若 0 4vgl= ，则 H=2l C．不论 v0 多大，可以肯定 H≤ 2 0 2 v g 总是成立的 D．上述说法都正确 10、水平放置的木柱，横截面为边长等于 a 的正四边形 ABCD；摆长 l =4a 的摆，悬挂在 A 点（如图 1—14 所示），开 始时质量为 m 的摆球处在与 A 等高的 P 点，这时摆线沿水平方向伸直；已知摆线能承受的最大拉力为 7mg；若以初速度．．．．．v．0． B A θ 图 1—11 图 1—12 v0 图 1—13 竖直向下将摆球从．．．．．．．．P．点抛出，为使摆球能始终沿圆弧运动，并最后击中．．．．．．．．．．．．．．．．．．．．．．A．点．．求 v0 的许可值范围（不计空气阻力）． 11、已知单摆 a 完成 10 次全振动的时间内，单摆 b 完成 6 次全振动，两摆长之差为 1.6m，则两摆长 al 与 bl 分别为（ ） A． 2.5m, 0.9mabll== B． 0.9m, 2.5mabll= = C． 2.4m, 4.0mabll== D． 4.0m, 2.4mabll= = 12、一列简谐横波沿直线传播，传到 P 点时开始计时，在 t=4s 时，P 点恰好完成了 6 次全振动，而在同一直线上的 Q 点完成了 12 4 次全振动，已知波长为 113 m3 ．试求 P、Q 间的距离和波速各多大． 13、如图 1—15 所示，小车板面上的物体质量为 m=8kg，它被一根水平方向上拉伸了 的弹簧拉住而静止在小车上，这时弹簧的弹力为 6N．现 沿水平向右的方向对小车施以作用 力，使小车由静止开始运动起来，运动中加速度由零逐渐 增大到 1m/s2，随即以 1m/s2 的加速 度做匀加速直线运动．以下说法中，正确的是（ ） A．物体与小车始终保持相对静止，弹簧对物体的作 用力始终没有发生变化 B．物体受到的摩擦力先减小、后增大、先向左、后 向右 C．当小车加速度（向右）为 0.75m/s2 时，物体不受摩擦力作用 D．小车以 1m/s2 的加速度向右做匀加速直线运动时，物体受到的摩擦力为 8N 14、如图 1—16 所示，一块质量为 M，长为 L 的均质板放在很长的光滑水平桌面上，板的左端有一质量为 m 的小物体 （可视为质点），物体上连接一根很长的细绳，细绳跨过位于桌边的定滑轮．某人以恒定的速率 v 向下拉绳，物体最多只能 到达板的中点，而板的右端尚未到达桌边定滑轮处．试求： 图 1—14 图 1—15 （1）物体刚达板中点时板的位移． （2）若板与桌面之间有摩擦，为使物体能达到板的右端，板与桌面之间的动摩擦因数的范围是多少． 15、在水平地面上有一质量为 2kg 的物体，物体在水平拉力 F 的作用下由静止开始运动，10s 后拉力大小减为 3 F ，该 物体的运动速度随时间变化的图像如图 1—17 所示，求： （1）物体受到的拉力 F 的大小； （2）物体与地面之间的动摩擦因数（g 取 10m/s2）． 16、如图所示，一高度为 h=0.8m 粗糙的水平面在 B 点处与一倾角为θ =30°的斜面 BC 连接，一小滑块从水平面上的 A 点以 v0=3m/s 的速度在粗糙的水平面上向右运动．运动到 B 点时小滑块恰能沿光滑斜面下滑．已知 AB 间的距离 S=5m， 求： （1）小滑块与水平面间的动摩擦因数． （2）小滑块从 A 点运动到地面所需的时间． （3）若小滑块从水平面上的 A 点以 v1=5m/s 的速度在粗糙的水平面上向右运动，运动到 B 点时小滑块将做什么运动？ 并求出小滑块从 A 点运动到地面所需时间（取 g=10m/s2）． v M m 图 1—16 v/m·s－1 t/ 2 4 6 8 2 4 6 8 10 12 14 16 O 图 1—17 h A B C θ 图 1—18 专题二 动量与机械能 黄冈中学：徐辉 命题导向 动量守恒与能量守恒是近几年高考理科综合物理命题的重点、热点和焦点，也是广大考生普遍感到棘手的难点之一．动 量守恒与能量守恒贯穿于整个高中物理学习的始终，是联系各部分知识的主线．它不仅为解决力学问题开辟了两条重要途径， 同时也为我们分析问题和解决问题提供了重要依据．守恒思想是物理学中极为重要的思想方法，是物理学研究的极高境界， 是开启物理学大门的金钥匙，同样也是对考生进行方法教育和能力培养的重要方面．因此，两个守恒可谓高考物理的重中之 重，常作为压轴题出现在物理试卷中，如 2004 年各地高考均有大题． 纵观近几年高考理科综合试题，两个守恒考查的特点是： ①灵活性强，难度较大，能力要求高，内容极丰富，多次出现在两个守恒定律网络交汇的综合计算中； ②题型全，年年有，不回避重复考查，平均每年有 3—6 道题，是区别考生能力的重要内容； ③两个守恒定律不论是从内容上看还是从方法上看都极易满足理科综合试题的要求，经常与牛顿运动定律、圆周运动、 电磁学和近代物理知识综合运用，在高考中所占份量相当大． 从考题逐渐趋于稳定的特点来看，我们认为：2005 年对两个守恒定律的考查重点仍放在分析问题和解决问题的能力 上．因此在第二轮复习中，还是应在熟练掌握基本概念和规律的同时，注重分析综合能力的培养，训练从能量、动量守恒的 角度分析问题的思维方法． 【典型例题】 【例 1】 （2001 年理科综合）下列是一些说法： ①一质点受到两个力作用且处于平衡状态（静止或匀速），这两个力在同一段时间内的冲量一定相同； ②一质点受两个力作用且处于平衡状态（静止或匀速），这两个力在同 一时间内做的功或者都为零，或者大小相等符号相反； ③在同样时间内，作用力力和反作用力的功大小不一定相等，但正负符号一定相反； ④在同样的时间内，作用力和反作用力的功大小不一定相等，正负号也不一定相反． 以上说法正确的是（ ） A．①② B．①③ C．②③ D．②④ 【例 2】 （石家庄）为了缩短航空母舰上飞机起飞前行驶的距离，通常用弹簧弹出飞机，使飞机获得一定的初速度， 进入跑道加速起飞．某飞机采用该方法获得的初速度为 v0，之后，在水平跑道上以恒定功率 P 沿直线加速，经过时间 t， 离开航空母舰且恰好达到最大速度 vm．设飞机的质量为 m，飞机在跑道上加速时所受阻力大小恒定．求： （1）飞机在跑道上加速时所受阻力 f 的大小； （2）航空母舰上飞机跑道的最小长度 s． 【例 3】 如下图所示，质量为 m=2kg 的物体，在水平力 F=8N 的作用下，由静止开始沿水平面向右运动．已知物体与 水平面间的动摩擦因数 μ =0.2．若 F 作用 t1=6s 后撤去，撤去 F 后又经 t2=2s 物体与竖直墙壁相碰，若物体与墙壁作用时间 t3=0.1s，碰墙后反向弹回的速度 v′ =6m/s，求墙壁对物体的平均作用力（g 取 10m/s2）． 【例 4】 有一光滑水平板，板的中央有一小孔，孔内穿入一根光滑轻线，轻线的上端系一质量为 M 的小球，轻线的下 端系着质量分别为 m1 和 m2 的两个物体，当小球在光滑水平板上沿半径为 R 的轨道做匀速圆周运动时，轻线下端的两个物 体都处于静止状态（如下图）．若将两物体之间的轻线剪断，则小球的线速度为多大时才能再次在水平板上做匀速圆周运动？ 【例 5】 如图所示，水平传送带 AB 长 l=8.3m，质量为 M=1kg 的木块随传送带一起以 v1=2m/s 的速度向左匀速运动（传 送带的传送速度恒定），木块与传送带间的动摩擦因数 μ =0.5．当木块运动至最左端 A 点时，一颗质量为 m=20g 的子弹以 0v− =300m/s 水平向右的速度正对射入木块并穿出，穿出速度 u=50m/s，以后每隔 1s 就有一颗子弹射向木块，设子弹射穿 木块的时间极短，且每次射入点各不相同，g 取 10m/s．求： （1）在被第二颗子弹击中前，木块向右运动离 A 点的最大距离？ （2）木块在传达带上最多能被多少颗子弹击中？ （3）从第一颗子弹射中木块到木块最终离开传送带的过程中，子弹、木块和传送带这一系统产生的热能是多少？（g 取 10m/s） v0 m A B M 【例 6】 质量为 M 的小车静止在光滑的水平面上，小车的上表面是一光滑的曲面，末端是水平的，如下图所示，小车 被挡板 P 挡住，质量为 m 的物体从距地面高 H 处自由下落，然后沿光滑的曲面继续下滑，物体落地点与小车右端距离 s0， 若撤去挡板 P，物体仍从原处自由落下，求物体落地时落地点与小车右端距离是多少？ 【例 7】 如下图所示，一辆质量是 m=2kg 的平板车左端放有质量 M=3kg 的小滑块，滑块与平板车之间的动摩擦因数 μ =0.4，开始时平板车和滑块共同以 v0=2m/s 的速度在光滑水平面上向右运动，并与竖直墙壁发生碰撞，设碰撞时间极短 且碰撞后平板车速度大小保持不变，但方向与原来相反．平板车足够长，以至滑块不会滑到平板车右端．（取 g=10m/s2）求 ： （1）平板车每一次与墙壁碰撞后向左运动的最大距离． （2）平板车第二次与墙壁碰撞前瞬间的速度 v． （3）为使滑块始终不会滑到平板车右端，平板车至少多长？ 【例 8】 如图所示，光滑水平面上有一小车 B，右端固定一个砂箱，砂箱左侧连着一水平轻弹簧，小车和砂箱的总质 量为 M，车上放有一物块 A，质量也是 M，物 块 A 随小车以速度 v0 向右匀速运动．物块 A 与左侧的车面的动摩擦因数为 μ ， 与右侧车面摩擦不计．车匀速运动时，距砂面 H 高处有一质量为 m 的泥球自由下落，恰好落在砂箱中，求： （1）小车在前进中，弹簧弹性势能的最大值． （2）为使物体 A 不从小车上滑下，车面粗糙部分应多长？ M m v0 m H A B v0 【跟踪练习】 1．物体在恒定的合力 F 作用下作直线运动，在时间△t1 内速度由 0 增大到 v，在时间△t2 内速度由 v 增大到 2v．设 F 在△ t1 内做的功是 W1，冲量是 I1；在△t2 内做的功是 W2，冲量是 I2，那么（ ） A． 1212,I IW W<= B． 1212,I IW W<< C． 1212,I IW W== D． 1212,I IW W=< 2．矩形滑块由不同材料的上、下两层粘在一起组成，将其放在光滑的水平面上，如图所示．质量为 m 的子弹以速度 v 水平 射向滑块．若射击上层，则子弹刚好不穿出；若射击下层，整个子弹刚好嵌入，则上述两种情况比较，说法正确的是（ ） ①两次子弹对滑块做功一样多 ②两次滑块所受冲量一样大 ③子弹嵌入下层过程中对滑块做功多 ④子弹击中上层过程中产生的热量多 A．①④ B．②④ C．①② D．②③ 3．如图所示，半径为 R，内表面光滑的半球形容器放在光滑的水平面上，容器左侧靠在竖直墙壁．一个质量为 m 的小物块， 从容器顶端 A 无初速释放，小物块能沿球面上升的最大高度距球面底部 B 的距离为 3 4 R ．求： （1）竖直墙作用于容器的最大冲量； （2）容器的质量 M． 4．离子发动机是一种新型空间发动机，它能给卫星轨道纠偏或调整姿态提供动力，其中有一种离子发动机是让电极发射的 电子撞击氙原子，使之电离，产生的氙离子经加速电场加速后从尾喷管喷出，从而使卫星获得反冲力，这种发动机通过 甲 乙 改变单位时间内喷出离子的数目和速率，能准确获得所需的纠偏动力．假设卫星（连同离子发动机）总质量为 M，每个 氙离子的质量为 m，电量为 q，加速电压为 U，设卫星原处于静止状态，若要使卫星在离子发动机起动的初始阶段能获 得大小为 F 的动力，则发动机单位时间内应喷出多少个氙离子？此时发动机动发射离子的功率为多大？ 5．如图所示，AB 为斜轨道，与水平方向成 45°角，BC 为水平轨道，两轨道在 B 处通过一段小圆弧相连接，一质量为 m 的 小物块，自轨道 AB 的 A 处从静止开始沿轨道下滑，最后停在轨道上的 C 点，已知 A 点高 h，物块与轨道间的滑动摩擦 系数为 μ ，求： （1）在整个滑动过程中摩擦力所做的功． （2）物块沿轨道 AB 段滑动时间 t1 与沿轨道 BC 段滑动时间 t2 之比值 1 2 t t ． （3）使物块匀速地、缓慢地沿原路回到 A 点所需做的功． 6．如图所示，粗糙的斜面 AB 下端与光滑的圆弧轨道 BCD 相切于 B，整个装置竖直放置，C 是最低点，圆心角∠BOC=37°， D 与圆心 O 等高，圆弧轨道半径 R=0.5m，斜面长 L=2m，现有一个质量 m=0.1kg 的小物体 P 从斜面 AB 上端 A 点无初速 下滑，物体 P 与斜面 AB 之间的动摩擦因数为 μ =0.25．求： （1）物体 P 第一次通过 C 点时的速度大小和对 C 点处轨道的压力各为多大？ （2）物体 P 第一次离开 D 点后在空中做竖直上抛运动，不计空气阻力，则最高点 E 和 D 点之间的高度差为多大？ （3）物体 P 从空中又返回到圆轨道和斜面，多次反复，在整个运动过程中，物体 P 对 C 点处轨道的最小压力为多大？ 7．如图所示，光滑水平面 AB 与竖直面内的半圆形导轨在 B 点衔接，导轨半径为 R．一个质量为 m 的静止物块在 A 处压缩 弹簧，在弹力的作用下获一向右的速度，当它经过 B 点进入导轨瞬间对导轨的压力为其重力的 7 倍，之后向上运动恰能 完成半圆周运动到达 C 点．求： （1）弹簧对物块的弹力做的功． （2）物块从 B 至 C 克服阻力做的功． （3）物块离开 C 点后落回水平面时其动能的大小． 8．（’03 全国高考，34）[理综·22 分]一传送带装置示意如下图，其中传送带经过 AB 区域时是水平的，经过 BC 区域时变 为圆弧形（圆弧由光滑模板形成，未画出），经过 CD 区域时是倾斜的，AB 和 CD 都与 BC 相切．现将大量的质量均为 m 的小货箱一个一个在 A 处放到传送带上，放置时初速为零，经传送带运送到 D 处，D 和 A 的高度差为 h．稳定工作时传 送带速度不变，CD 段上各箱等距排列，相邻两箱的距离为 L．每个箱子在 A 处投放后，在到达 B 之前已经相对于传送带 静止，且以后也不再滑动（忽略经 BC 段时的微小滑动）．已知在一段相当长的时间 T 内，共运送小货箱的数目为 N．这 装置由电动机带电，传送带与轮子间无相对滑动，不计轮轴处的摩擦．求电动机的平均输出功率 P ． 9．如图所示，质量 M=0.45kg 的带有小孔的塑料块沿斜面滑到最高点 C 时速度恰为零，此时与从 A 点水平射出的弹丸相碰， 弹丸沿着斜面方向进入塑料块中，并立即与塑料块有相同的速度．已知 A 点和 C 点距地面的高度分别为：H=1.95m， h=0.15m，弹丸的质量 m=0.050kg，水平初速度 v0=8m/s，取 g=10m/s2．求： （1）斜面与水平地面的夹角θ．（可用反三角函数表示） （2）若在斜面下端与地面交接处设一个垂直于斜面的弹性挡板，塑料块与它相碰后的速率等于碰前的速率，要使塑料 块能够反弹回到 C 点，斜面与塑料块间的动摩擦因数可为多少？ 10．（’04 江苏，18）（16 分）一个质量为 M 的雪橇静止在水平雪地上，一条质量为 m 的爱斯基摩狗站在雪橇上．狗向雪橇 的正后方跳下，随后又追赶并向前跳上雪橇；其后狗又反复地跳下、追赶并跳上雪橇．狗与雪橇始终沿一条直线运动．若 狗跳离雪橇时雪橇的速度为 V，则此时狗相对于地面的速度为 V＋u（其中 u 为狗相对于雪橇的速度，V＋u 为代数和， 若以雪橇运动的方向为正方向，则 V 为正值，u 为负值．）设狗总以速度 v 追赶和跳上雪橇，雪橇与雪地间的摩擦忽略 不计．已知 v 的大小为 5m/s，u 的大小为 4m/s，M=30kg，m=10kg． （1）求狗第一次跳上雪橇后两者的共同速度的大小． （2）求雪橇最终速度的大小和狗最多能跳动上雪橇的次数． （供使用但不一定用到的对数值：lg2=0.301，lg3=0.477） 11．（汕头）如下图所示，光滑水平面上，质量为 m 的小球 B 连接着轻质弹簧，处于静止状态，质量为 2m 的小球 A 以大小 为 v0 的初速度向右运动，接着逐渐压缩弹簧并使 B 运动，过一段时间，A 与弹簧分离． （1）当弹簧被压缩到最短时，弹簧的弹性势能 Ep 多大？ （2）若开始时在 B 球的右侧某位置固定一块挡板，在 A 球与弹簧未分离前使 B 球与挡板发生碰撞，并在碰后立刻将挡 板撤走．设 B 球与挡板的碰撞时间极短，碰后 B 球的速度大小不变但方向相反．欲使此后弹簧被压缩到最短时， 弹簧势能达到第（1）问中 Ep 的 2.5 倍，必须使 B 球在速度多大时与挡板发生碰撞？ 12．（’00 全国高考，22 ）[天津江西·14 分]在原子核物理中，研究核子与核子关联的最有效途径是“双电荷交换反应”．这 类反应的前半部分过程和下述力学模型类似．两个小球 A 和 B 用轻质弹簧相连，在光滑的水平直轨道上处于静止状态．在 它们左边有一垂直于轨道的固定挡板 P，右边有一个小球 C 沿轨道以速度 v0 射向 B 球，如图所示．C 与 B 发生碰撞并立即 结成一个整体 D．在它们继续向左运动的过程中，当弹簧长度变到最短时，长度突然被锁定，不再改变．然后，A 球与挡板 P 发生碰撞，碰后 A、D 都静止不动，A 与 P 接触而不粘连．这一段时间，突然解除锁定（锁定及解除锁定均无机械能损失）．已 知 A、B、C 三球的质量为 m． （1）求弹簧长度刚被锁定后 A 球的速度； （2）求在 A 球离开挡板 P 之后的运动过程中，弹簧的最大弹性势能． 13．（广州）用轻弹簧相连的质量均为 2kg 的 A、B 两物块都以 v=6m/s 的速度在光滑的水平地面上运动，弹簧处于原长， 质量 4kg 的物块 C 静止在前方，如下图所示．B 与 C 碰撞后二者粘在一起运动．求：在以后的运动中： （1）当弹簧的弹性势能最大时物体 A 的速度多大？ （2）弹性势能的最大值是多大？ （3）A 的速度有可能向左吗？为什么？ 14．（’04 广东，17）（16 分）图中，轻弹簧的一端固定，另一端与滑块 B 相连，B 静止在水平直导轨上，弹簧处在原长状态．另 一质量与 B 相同的滑块 A，从导轨上的 P 点以某一初速度向 B 滑行．当 A 滑过距离 l1 时，与 B 相碰，碰撞时间极短，碰后 A、B 紧贴在一起运动，但互不粘连．已知最后 A 恰好返回到出发点 P 并停止．滑块 A 和 B 与导轨的滑动摩擦因数都为 μ ， 运动过程中弹簧最大形变量为 l2，重力加速度为 g．求 A 从 P 点出发时的初速度 v0． 15．（’01 春季招生，22）（14 分）如下图所示，A、B 是静止在水平地面上完全相同的两块长木板．A 的左端和 B 的右面端 相接触．两板的质量皆为 M=2.0kg，长度皆为 l=1.0m．C 是一质量为 m=1.0kg 的小物块．现给它一初速度 v0=2.0m/s， 使它从 B 板的左端开始向右滑动，已知地面是光滑的，而 C 与 A、B 之间的动摩擦因数为 μ =0.10．求最后 A、B、C 各 以多大的速度做匀速运动．（取重力加速度 g=10m/s2） 16．如图所示，一个长为 L，质量为 M 的长方形木块，静止在光滑水平面上，一个质量为 m 的物块（可视为质点），以水平 初速度 v0，从木块的左端滑向另一端，设物块与木块间的动摩擦因数为 μ ，当物块与木块达到相对静止时，物块仍在 长木块上，求系统机械能转化成内能的量 Q． B A v0 C 专题三 电场和磁场 黄冈中学：江楚桥 【方法归纳】 一、场强、电势的概念 1、电场强度 E ①定义：放入电场中某点的电荷受的电场力 F 与它的电量 q 的比值叫做该点的电场强度。 ②数学表达式： qFE /= ，单位： mV / ③电场强度 E 是矢量，规定正电荷在电场中某点所受电场力的方向即为该点的电场强度的方向 ④场强的三个表达式 定义式 决定式 关系式 表达式 qFE /= r kQE = d UE = 选用 范围 对任何电场E的大小及 方向都适用。与检验电 荷的电量的大小、电性 及存在与否无关。 q：是检验电荷 只对真空的点电荷适用。 Q：是场源电荷的电量。 r：研究点到场源电荷的距 离。 只对匀强电场适用。 U：电场中两点的电势差。 d：两点间沿电场线方向的距 离。 说明 电场强度是描述电场力的性质的物理量。电场 E 与 F、q 无关，取决于电场本身。 当空间某点的电场是由几个点电荷共同激发的，则该点的电场强度等于每个点电 荷单独存在时所激发的电场在该点的场强的矢量和。 ⑤比较电场中两点的电场强度的大小的方法： 由于场强是矢量。比较电场强度的大小应比较其绝对值的大小，绝对值大的场强就大，绝对值小的场强就小。 Ⅰ在同一电场分布图上，观察电场线的疏密程度，电场线分布相对密集处，场强较大；电场较大；电场线分布相对稀疏 处，场强较小。 Ⅱ形成电场的电荷为点电荷时，由点电荷场强公式 2r kQE = 可知，电场中距这个点电荷 Q 较近的点的场强比距这个点 电荷 Q 较远的点的场强大。 Ⅲ匀强电场场强处处相等 Ⅳ等势面密集处场强大，等势面稀疏处场强小 2、电势、电势差和电势能 ①定义： 电势：在电场中某点放一个检验电荷 q，若它具有的电势能为 E，则该点的电势为电势能与电荷的比值。电场中某点的 电势在数值上等于单位正电荷由该点移到零电势点时电场力所做的功。也等于该点相对零电势点的电势差。 电势差：电荷在电场中由一点 A 移到另一点 B 时，电场力做功 ABW 与电荷电量 q 的比值，称为 AB 两点间的电势差， 也叫电压。 电势能：电荷在电场中所具有的势能；在数值上等于将电荷从这一点移到电势能为零处电场力所做的功。 ②定义式： q EU = 或 q WU AB AB = ，单位：V UqE = 单位：J ③说明：Ⅰ电势具有相对性，与零电势的选择有关，一般以大地或无穷远处电势为零。 Ⅱ电势是标量，有正负，其正负表示该的电势与零电势的比较是高还是低。 Ⅲ电势是描述电场能的物理量， ④关于几个关系 关于电势、电势差、电势能的关系 电势能是电荷与电场所共有的；电势、电势差是由电场本身因素决定的，与检验电荷的有无没有关系。 电势、电势能具有相对性，与零电势的选择有关；电势差具有绝对性，与零电势的选择无关。 关于电场力做功与电势能改变的关系 电场力对电荷做了多少功，电势能就改变多少；电荷克服电场力做了多少功，电势能就增加多少，电场力对电荷做了多 少正功，电势能就减少多少，即 EW Δ−= 。 在学习电势能时可以将“重力做功与重力势能的变化”作类比。 关于电势、等势面与电场线的关系 电场线垂直于等势面，且指向电势降落最陡的方向，等势面越密集的地方，电场强度越大。 ⑤比较电荷在电场中某两点的电势大小的方法： Ⅰ利用电场线来判断：在电场中沿着电场线的方向，电势逐点降低。 Ⅱ利用等势面来判断：在静电场中，同一等势面上各的电势相等，在不同的等势面间，沿着电场线的方向各等势面的电 势越来越低。 Ⅲ利用计算法来判断：因为电势差 q WU ab ab = ，结合 baab UUU −= ，若 0>abU ，则 ba UU > ，若 0=abU ，则 ba UU = ； 若 0 1T B. 2T < 1T C. 2T = 1T D. 2T = 1T = mg 4．有三根长度皆为 ml 00.1= 的不可伸长的绝缘轻线，其中两根的一端固定在天花板上的 O 点，另一端分别拴有质量皆 为 kgm 21000.1 −×= 的带电小球 A 和 B，它们的电量分别为 q− 和 q+ ， Cq 71000.1 −×= 。A、B 之间用第三根 线连接起来。空间中存在大小为 CNE /1000.1 6×= 的匀强电场，场强方向沿水平向右，平衡时 A、B 球的位置如图 13 所示。现将 O、B 之间的线烧断，由于有空气阻力，A、B 球最后会达到新的平衡位置。求最后两球的机械能与电势 能的总和与烧断前相比改变了多少。（不计两带电小球间相互作用的静电力） 图 12 图 13 O A B -q q E O A B Q m，q 5．如图 14 所示，电子在电势差为 U1 的加速电场中由静止开始运动，然后射入电势差为 U2 的两平行极板间的电场中，射入 方向与极板平行，整个装置处在真空中，重力 可忽略，在满足电 子能射出平行板区的条件下，下述四种情况 中，一定能使电子 的偏转角θ 变大的是（ ） A.U1 变大，U2 变大 B.U1 变小，U2 变大 C.U1 变大，U2 变小 D.U1 变小，U2 变小 6．（1997 年，全国题）如图 15（1）所示，真空室中电极 K 发出的电子（初速不计）经过 10000 =U 伏的加速电场后， 由小孔 S 沿两水平金属板 A、B 间的中防线射入，A、B 板长 02.0=l 米，相距 020.0=d 米，加在 A、B 两板间的电压 u 随时间 t 变化 u—t 图线如图 15(2)所示，设 A、B 间的电场可看作是均匀的，且两板外无电场，在每个电子通过电场区 域的极短时间。内，电场可视作恒定的。两板右侧放一记录圆筒，筒的左侧边缘与极右端距离 15.0=b 米，筒绕其竖直 轴匀速转动，周期 T 20.0= 秒，筒的周长 20.0=s 米，筒能接收到通过 A、B 板的全部电子。 （1）以 t=0 时[见图 15（2）]，此时 u=0，电子打到圆筒记录纸上的点作为 xy 坐标系的原点，并取 y 轴竖直向上， 试计算电子打到记录纸上的最高点的 y 坐标和 x 坐标。（不计重力作用） （2）在给出的坐标纸图 15（3）上定量地画出电子打到记录纸上的点形成的图线。 图 14 l A B S U0 k b d 图 15(1) 0 1 2 3 4 5 t 10-1s y/cm x/cm 0 -5 5 10 20 图 15(2) 图 15(3) U1 U2 θ 7．(1997 年，全国题)在图 16 中所示的实验装置中，平行板电 容器的极板 A 与灵 敏的静电计相接，极板 B 接地，若极板 B 稍向上移动一点， 由观察到的静电计 指针变化作出平行板电容器电容变小的结论，其依据是 （ ） A.两极板间的电压不变，极板上的电量变小 B.两极板间的电压不变，极板上的电量变大 C.极板上的电量几乎不变，两极板间的电压变小 D.极板上的电量几乎不变，两极板间的电压变大 8．如 图 17 所示，已充电的平行板电容器，带正电的极板接地， 两极板间于 P 点处 固定一负的点电荷，若将上极板下移至虚线位置，则 下列说法中正确的是 （ ） A.两极间的电压和板间场强都变小 B.两极间的电压变小，但场强不变 C.P 点的电势升高，点电荷的电势能增大 D.P 点的电势不变，点电荷的电势能也不变 9．如图 18 所示，在 x 轴上方有匀强磁场（磁感强度为 B），一个质量为 m， 带电量为 q 的粒子以速度 v0 从坐标原点 O 射入磁场，v0 与 x 轴的负方向夹角为θ ，不计重力，求粒子在磁场中飞行的时 间和飞出磁场的坐标（磁场垂直纸面，不考虑粒子的重力） 10．如图 19 所示，x 轴上方有匀强磁场， 磁感应强度为 B，方向如图所示，下方有匀强电场，场强为 E。今有电量为 q， 质量为 m 的粒子位于 y 轴 N 点坐标（0，－b）。不计粒子所受重力。在 x 轴上有一点 M（L，0）。若使上述粒子在 y 轴 上的 N 点由静止开始释放在电磁场中往返运动，刚好能通过 M 点。已知 OM＝L。求： (1) 粒子带什么电? (2) 释放点 N 离 O 点的距离须满足什么条件? 图 16 图 17 图 18 A B • P O θ v0 (3) 从 N 到 M 点粒子所用最短时间为多少? 11．图 20 中，A、B 是一对平行的金属板。在两板间加上一周期 为 T 的交变电压 u 。A 板的电势 UA=0，B 板的电势 UB 随时间的变化规律为， 在 0 到 T/2 的时间 内，UB= U0(正常数)；在 T/2 到达 T 的时间内，UB＝－U0；在T到3T/2的时间 内，UB=U0；在 3T/2 到 2T 的时间，UB= —U0…现有一电子 从 A 板上的小孔进 入两板间的电场区内，设电子的初速度和重力影响均可忽 略，则（ ） A.若电子在 t＝0 时刻进入，它将一直向 B 板运动 B.若电子是在 t＝T/8 时刻进入的，它可能时而向 B 板运动， 时而向 A 板运动， 最后打在 B 板上 C.若电子是在 t＝3T/8 时刻进入的，它可能时而向 B 板运动，时而向 A 板运动，最后打在 B 板上 D.若电子是在 t＝T/2 时刻进入的，它可能时而向 B 板，时而向 A 板运动 12. (2003.江苏)串列加速器是用来产生高能离子的装置。图 21 中虚线框内为其主体的原理示意图，其中加速管的中部 b 处 有很高的正电势 U，a、c 两端均有电极接地（电势为零），现将速度很低的负一价碳离子从 a 端输入，当离子到达 b 处时， 可被设在 b 处的特殊装置将其电子剥离，成为 n 价正离子，而不改变其速度大小。这些正 n 价碳离子从 c 端飞出后进入 一与其速度方向垂直的、磁感应强度为 B 的匀强磁场中，在磁场中做半径为 R 的圆周运动。已知碳离子的质量 kgm 26100.2 −×= ， VU 5105.7 ×= ， TB 50.0= ， 2=n ，元电荷 Ce 19106.1 −×= ，求半径 R。 图 19 图 20 图 21 加速管 a b c l B A y xM N 0,- L,0 O 13．如图 22 所示为一种获得高能粒子的装置。环形区域内存在垂直纸面向外、大小可调的匀强磁场。质量为 m，电量为＋ q 的粒子在环中作半径为 R 的圆周运动。A、B 为两块中心开有小孔的极板。原来电势都是零，每当粒子飞经 A 板时，A 板 电势升高为＋U，B 板电势仍保持为零，粒子在两板间电场中得到加速。每当粒子离开 B 板时，A 板电势又降为零。粒子在 电场一次次加速下动能不断增大，而绕行半径不变。 (1)设 t＝0 时粒子静止在 A 板小孔处，在电场作用下加速，并绕行第一圈。求粒子绕行 n 圈回到 A 板时获得的总动能 En。 (2)为使粒子始终保持在半径为 R 的圆轨道上运动，磁场必须周期性递增。求粒子绕行第 n 圈时的磁感应强度 Bn。 (3)求粒子绕行 n 圈所需要的总时间 tn（设极板间距离远小于 R）。 (4)在图 22(2)中画出 A 板电势 u 与时间 t 的关系（从 t＝0 起画到粒子第四次离开 B 板时即可） (5)在粒子绕行的整个过程中，A 板电势是否可始终保持为＋U？为什么？ 14．（2002 年，广东题）如图 23（a）所示，A、B 为水平放置的平行金属板，板间距离为 d （ d 远小于板的长度和宽）， 在两板之间有一带负电的质点 P，已知若在 A、B 间加电压 U0，则 P 点可以静止平衡，现在 A、B 间加上图（b）所示的 随时间 t 变化的电压 U，在 0=t 时，质点 P 位于 A、B 的中点处且初速度为零，已知质点 P 能在 A、B 间以最大的幅度 R O A +U 0 图 22(1) u U 0 t 图 22(2) 上下运动，而又不与两极板相碰，求图（b）中 U 改变的各时刻 321 ,, ttt 及 nt 的表达式（质点开始从中点上升到最高点， 及以后每次从最高点到最低点或从最低点到最高点的过程，电压只改变一次）。 15．如图 24 所示，倾角为 300 的直角三角形底边长为 2l，底边外在水平位置，斜边为光滑绝缘导轨，现在底边中点 O 处固 定一正电荷 Q，让一个质量为 m 的带正电荷 q 从斜面顶端 A 沿斜面滑下（始终不脱离斜面），已测得它滑到仍在斜边上的 垂足 D 处的速度为 v，加速度为 a，方向沿斜面向下，问该质点滑到斜边底端 C 点时的速度和加速度各为多少？ 专题四 电磁感应与电路 黄冈中学 王小兰 [方法归纳] 电磁感应是电磁学中最为重要的内容，也是高考的热点之一。电磁感应是讨论其他形式能转化为电能的特点和规律；电 路问题主要是讨论电能在电路中传输、分配并通过用电器转化成其他形式能的特点和规律，本专题的思想是能量转化与守恒 （a） （b） 图 23 图 24 0 t1 t2 t3 t4 tn t u 2U0 ·P + — A B O +Q 300 A B D E 思想。 在复习电磁感应部分时，其核心是法拉第电磁感应定律和楞次定律；这两个定律一是揭示感应电动势的大小所遵循的规 律；一个是揭示感的电动势方向所遵循的规律，法拉第电磁感定律的数学表达式为： n tε ΔΦ= Δ ，磁通量的变化率越大，感 应电动势越大．磁通量的变化率越大，外界所做的功也越大．楞次定律的表述为：感应电流的磁场总要阻碍引起感应电流的 磁通量的变化，从楞次定律的内容可以判断出：要想获得感应电流就必须克服感应电流的阻碍，需要外界做功，需要消耗其 他形式的能量．在第二轮复习时如果能站在能量的角度对这两个定律进行再认识，就能够对这两个定律从更加整体、更加深 刻的角度把握． 电路部分的复习，其一是以部分电路欧姆定律为中心，包括六个基本物理量（电压、电流、电阻、电功、电功率、电热）， 三条定律（部分电路欧姆定律、电阻定律和焦耳定律），以及串、并联电路的特点等概念、定律的理解掌握和计算；其二是 以闭合电路欧姆定律为中心讨论电动势概念、闭合电路中的电流、路端电压以及闭合电路中能量的转化；其三，对高中物理 所涉及的三种不同类别的电路进行比较，即恒定电流电路、变压器电路、远距离输电电路，比较这些电路哪些是基本不变量， 哪些是变化量，变化的量是如何受到不变量的制约的．其能量是如何变化的． 在恒定电流电路中，如果题目不加特殊强调，电源的电动势和内电阻是基本不变量，在外电阻改变时其他量的变化受到 基本不变量的制约． 在变压器电路中，如果题目不加特殊强调，变压器的输入电压不变，其他量改变时受到这个基本不变量的制约． 在远距离输电电路中，如果题目不加特殊强调，发电厂输出的电功率不变，其他量改变时受到这个基本不变量的制约． [典例分析] 1．电磁感应的图象问题 方法：图象问题有两种：一是给出电磁感应过程选出或画出正确图象；二是由给定的有关图象分析电磁感应过程，求解 相应的物理量．其思路是：利用法拉第电磁感应定律计算感应电动势．感应电流的大小，利用楞次定律或右手定则判定感应 电流的方向，利用图象法直观，明确地表示出感应电流的大小和方向．掌握这种重要的物理方法． 例 1、如图 4—1（a）所示区域（图中直角坐标系 xOy 的 1、3 象限）内有匀强磁场，磁感应强度方向垂直于图面向里， 大小为 B，半径为 l，圆心角为 60°的扇形导线框 OPQ 以角速度ω 绕 O 点在图面内沿逆时针方向匀速转动，导线框回路电 阻为 R． （1）求线框中感应电流的最大值 I0 和交变感应电流的频率 f． （2）在图（b）中画出线框转一周的时间内感应电流 I 随时间 t 变化的图象．（规定在图（a）中线框的位置相应的时刻 为 t =0） （a） （b） 图 4—1 2π ω 2、电路的动态分析 方法：利用欧姆定律，串、并联电路的性质，闭合电路的欧姆定律；明确不变量，以“从局部到整体再到局部”，“从外 电路到内电路再到外电路”的顺序讨论各物理量的变化情况． 例 2、如图 4—3 所示的电路中，电源的电动势 为 E，内阻为 r．当可变电阻的滑 片 P 向 b 移动时，电压表 V1 的读数 U1 与电压表 V2 的读数 U2 的变化情况是 （ ） A．U1 变大，U2 变小 B．U1 变大，U2 变大 C．U1 变小，U2 变小 B．U1 变小，U2 变大 3、电磁感应与力学综合 方法：从运动和力的关系着手，运用牛顿第二定 律 （1）基本思路：受力分析→运动分析→变化趋向→确定运动过程和最终的稳定状态→由牛顿第二定律列方程求解． （2）注意安培力的特点： （3）纯力学问题中只有重力、弹力、摩擦力，电磁感应中多一个安培力，安培力随速度变化，部分弹力及相应的摩擦 力也随之而变，导致物体的运动状态发生变化，在分析问题时要注意上述联系． 例 3、如图 4—4 所示，两根相距为 d 的足够长的平行金属导轨位于水平 xOy 平面内，左端接有阻值为 R 的电阻，其他 部分的电阻均不计．在 x>0 的一侧存在垂直 xOy 平面且方向竖直向下的稳定磁场，磁感强度大小按 B=kx 规律变化（其中 k 是一大于零的常数）．一根质量为 m 的金属杆垂直跨搁在光滑的金属导轨上，两者接触良好． 当 t =0 时直杆位于 x=0 处，其速度大小为 v0，方向沿 x 轴正方向，在此后的过程中，始终有一个方向向左的变力 F 作 用于金属杆，使金属杆的加速度大小恒为 a，加速度方向一直沿 x 轴的负方向．求： （1）闭合回路中感应电流持续的时间有多长？ （2）当金属杆沿 x 轴正方向运动的速度为 0 2 v 时，闭合回路的感应电动势多大？此时作用于金属杆的外力 F 多大？ 导体运动 v 感应电动势 E 感应电流 I 安培力 F 磁场对电流的作用 电磁感应 阻碍 闭合电路 欧姆定律 图 4—3 图 4—4 4、电磁感应与动量、能量的综合 方法： （1）从动量角度着手，运用动量定理或动量守恒定律 ①应用动量定理可以由动量变化来求解变力的冲量，如在导体棒做非匀变速运动的问题中，应用动量定理可以解决牛顿 运动定律不易解答的问题． ②在相互平行的水平轨道间的双棒做切割磁感线运动时，由于这两根导体棒所受的安培力等大反向，合外力为零，若不 受其他外力，两导体棒的总动量守恒．解决此类问题往往要应用动量守恒定律． （2）从能量转化和守恒着手，运用动能定律或能量守恒定律 ①基本思路：受力分析→弄清哪些力做功，正功还是负功→明确有哪些形式的能量参与转化，哪增哪减→由动能定理或 能量守恒定律列方程求解． ②能量转化特点：其它能（如：机械能） ⎯⎯⎯⎯⎯⎯→安培力做负功 电能 ⎯⎯⎯⎯⎯→电流做功 内能（焦耳热） 例 4、如图 4—6 所示，在空间中有一水平方向的匀强磁场区域，区域的上下边缘间距为 h，磁感应强度为 B．有一宽度 为 b（ba）处以 速度 v 沿抛物线下滑，假设抛物线足够长，金属环沿抛物 线下滑后产生的焦耳热总量是 （ ） A．mgb B． 21 2 mv C．mg(b－a) D． 21()2mg b a mv−+ 8．如图 4—20 所示，长为 L、电阻 r=0.3Ω、质量 m=0.1kg 的金属棒 CD 垂直跨搁在 位于水平面上的两条平行光滑金属导轨上，两 导轨间距也是 L，棒与导轨间接触良 好，导轨电阻不计，导轨左端接有 R=0.5Ω的电 阻，量程为 0～3.0A 的电流表串接在 一条导轨上，量程为 0～1.0V 的电压表接在电 阻 R 的两端，垂直导轨平面的匀强磁 场向下穿过平面．现以向右恒定外力 F 使金属 棒右移，当金属棒以 v=2m/s 的速度 在导轨平面上匀速滑动时，观察到电路中的一 个电表正好满偏，而另一个电表未满 偏，问： （1）此满偏的电表是什么表？说明理由． （2）拉动金属棒的外力 F 多大？ （3）此时撤去外力 F，金属棒将逐渐慢下来，最终停止在导轨上．求从撤去外力到金属棒停止运动的过程中通过电阻 R 的电量． 9．高频焊接是一种常用的焊接方法，其焊接的原理如图所示．将半径为 10cm 的待焊接的圆形金属工件放在导线做成的 1000 匝线圈中，然后在线圈中通以高频的交变电流，线圈产生垂直于金属工件所在平面的变化磁场，磁场的磁感应强度 B 的 变化率为 1000 2sintπ ω T/s．焊接处的接触电阻为工件非焊接部分电阻的 99 倍．工作非焊接部分每单位长度上的电 阻为 31 0 10 mR π−−=Ω ，焊接的缝宽非常小，求焊接过程中焊接处产生的热功率．（取 2π =10，不计温度变化对电阻的 图 4—19 图 4—20 影响） 图 4—21 10．如图所示，与光滑的水平平行导轨 P、Q 相连的电路中，定值电阻 R1=5Ω，R2=6Ω；电压表的量程为 0～10V，电流表 的量程为 0～3A，它们都是理想电表；竖直向下的匀强磁场穿过水平导轨面，金属杆 ab 横跨在导轨上，它们的电阻均 可不计，求解下列问题： （1）当滑动变阻器的阻值 R0=30Ω时，用水平恒力 F1=40N 向右作用于 ab，在 ab 运动达到稳定状态时，两个电表中有 一个电表的指针恰好满偏，另一个电表能安全使用．试问：这时水平恒力 F1 的功率多大？ab 的速度 v1 多大？ （2）将滑动变阻器的电阻调到 R0=3Ω，要使 ab 达到稳定运动状态时，两个电表中的一个电表的指针恰好满偏，另一 个电表能安全使用，作用于 ab 的水平恒力 F2 多大？这时 ab 的运动速度 v2 多大？ 11．两只相同的电阻，分别通过简谐波形的交流 电和方形波的交流电．两种交变电 流的最大值相等，波形如图 4—23 所示．在 简谐波形交流电的一个周期内，简 谐波形交流电在电阻上产生的焦耳热 Q1 与 方波形交流电在电阻上产生的焦 耳热 Q2 之比为 1 2 Q Q 等于（ ） A．3︰1 B．1︰2 C．2︰1 D．4︰3 12．曾经流行过一种向自行车车头灯供电的小型 交流发电机，图 4—24 甲为其结构 示意图．图中 N、S 是一对固定的磁极，abcd 为固定在转轴上的矩形线框，转轴过 bc 边中点、与 ab 边平行，它的一端有 一半径 r0=1.0cm 的摩擦小轮，小轮与自行车车轮的边缘相接触，如图 4—24 乙所示．当车轮转动时，因摩擦而带动小轮转 图 4—22 R0 Rx R1 图 4—23 动，从而使线框在磁极间转动．设线框由 N=800 匝导线圈组成，每匝线圈的面积 S=20cm2，磁极间的磁场可视为匀强磁场， 磁感强度 B=0.010T，自行车车轮的半径 R1=35cm，小齿轮的半径 R2=4.0cm，大齿轮的半径 R3=10.0cm（见图乙）．现从静 止开始使大齿轮加速运动，问大齿轮的角速度为多大时才能使发电机输出电压的有效值 U=3.2V？（假定摩擦小轮与自行车 轮之间无相对滑动） 图 4—24 13．如图 4—25 所示，两块水平放置的平行金属板间距为 d，定值电阻的阻值为 R，竖直放置线圈的匝数为 n，绕制线圈导 线的电阻为 R，其他导线的电阻忽略不计．现在竖直向上的磁场 B 穿过线圈，在两极板中一个质量为 m，电量为 q，带 正电的油滴恰好处于静止状态，则磁场 B 的变化情况是（ ） A．均匀增大，磁通量变化率的大小为 2mgd nq B．均匀增大，磁通量变化率的大小为 mgd nq C．均匀减小，磁通量变化率的大小为 2mgd nq D．均匀减小，磁通量变化率的大小为 mgd nq 14．如图 4—26 所示，水平面中的光滑平行导轨 P1、P2 相距 l=50cm，电池电动势 E′=6V，电阻不计；电容 C=2 μ F，定值 电阻 R=9Ω；直导线 ab 的质量 m=50g，横放在平行导轨上，其中导轨间的电阻 R′=3Ω；竖直向下穿过导轨面的匀强磁 场的磁感应强度 B=1.0T；导轨足够长，电阻不计． （1）闭合开关 S，直导线 ab 由静止开始运动的瞬时加速度多大？ab 运动能达到的最大速度多大？ （2）直导线 ab 由静止开始运动到速度最大的过程中，电容器的带电荷量变化了多少？ 图 4—25 E′ P1 P2 图 4—26 15．如图 4—27 所示的四个图中，a、b 为输入端，接交流电源、cd 为输出端，下列说法中错误．．的是（ ） A B C D A．A 图中 UabUcd C．C 图中 UabUcd 16．某电站输送的电功率是 500kW，当采用 6kV 电压输电时，安装在输电线路起点的电度表和终点的电度表一昼夜读数相 差 4800kWh（即 4800 度），试求：（1）输电线的电阻；（2）若要使输电线上损失的功率降到输送功率的 2.304%，应采 用多高的电压向外输电？ 专题五 物理实验 黄冈中学 丁汝辉 自然科学是实验性科学，物理实验是物理学的重要组成部分．理科综合对实验能力提出了明确的要求，即是“设计和完 成实验的能力”，它包含两个方面： 1．独立完成实验的能力．包括： （1）理解实验原理、实验目的及要求； （2）掌握实验方法步骤； （3）会控制实验条件和使用实验仪器，会处理实验安全问题； （4）会观察、解释实验现象，会分析、处理实验数据； （5）会分析和评价实验结果，并得出合理的实验结论． 2．设计实验的能力．能根据要求灵活运用已学过的物理理论、实验方法和仪器，设计简单的实验方案并处理相关的实 验问题．　 一、基本仪器的使用 ［方法归纳］ 1．要求会正确使用的仪器　 刻度尺、游标卡尺、螺旋测微器、天平、秒表、打点计时器、弹簧秤、温度表、电流表、电压表、多用电表、滑动变阻 器、电阻箱、示波器．　 2．在力学和电学实验中，常需要利用测量工具直接测量基本物理量． 基本物理量 测量仪器 长度 刻度尺、游标卡尺、螺旋测微器 时间 秒表（停表）、打点计时器 力学 质量 天平 ～ a b c d ～ a b d c ～ a b c d ～ a b d c 电阻（粗测） 欧姆表、电阻箱 电流 电流表 电学 电压 电压表 3．读数方法：　 用各种测量仪器测量有关物理量，读数时首先要弄清测量仪器的精度．以螺旋测微器为例：精度为 0.5 50 mm=0.01mm， 其读数方法是：读数=固定刻度数(含半毫米刻度)＋可动刻度数（含估读刻度数）×精度． [典例分析] 【例 1】 请将下列各种测量仪器的读数填在题中的横线上．　 示数___________cm 示数 示数___________s 示数__________s 【特别提示】 一般来说，除游标卡尺、秒表、电阻箱外，其他测量仪器的读数都需要估读，即读到精度的下一位．　 二、独立完成实验 ［方法归纳］ 1．常见间接测量的物理量及其测量方法　 有些物理量不能由测量仪器直接测量，这时，可利用待测量和可直接测量的基本物理量之间的关系，将待测物理量的测 量转化．．为基本物理量的测量． 待测物理量 基本测量方法 速度 ①利用纸带， 1 2 nn m SSv T ++= ；②利用平抛， 2 gvx y= 加速度 ①利用纸带，逐差法 2 Sa T Δ= ；②利用单摆 2 2 4 Lg T π= 力 根据 F=ma 转化为测量 m、a 力学 功 根据 kWE=Δ 转化为测量 m、S、v 电阻（精确测量） ①根据 UR I= 转化为测量 U、I（伏安法）；②电阻箱（半偏、替代） 电功率 根据 P=IU 转化为测量 U、I 电学 电源电动势 根据 E＝U＋Ir 转化为测量 U、I 2．处理实验数据的常用方法　 为了减小由于实验数据而引起的偶然误差，常需要采用以下方法进行处理．　 （1）多次测量求平均值；（2）图象法　 3．实验误差的分析　 中学物理中只要求初步了解系统误差和偶然误差、绝对误差和相对误差的概念；能定性分析某些实验中产生误差的主要 原因；知道用平均值法、图象法减小偶然误差；但不要求计算误差．　 （1）系统误差和偶然误差：测量值总是有规律的朝着某一方向偏离真值（总是偏大或总是偏小）的误差，称为系统误 此时待测电阻为___________Ω 电阻箱连入电路中的 电阻为___________Ω 用 0～0.6A 档，此电流 表示数为___________A 用 0～15V 档，此电压 表示数为___________V 差．系统误差的主要来源是仪器本身不够精确，或实验原理、方法不够完善．由于偶然因素的影响，造成测量值的无规则起 伏称为偶然误差．偶然误差是由于各种偶然因素对实验者、测量仪器，被测物理量的影响而产生的，多次测量偏大和偏小的 机会相同，因此，多次测量求平均值可减小偶然误差．　 （2）绝对误差和相对误差：设某物理量的真值为 A0 ，测量值为 A，则绝对误差 0||A AΔ= − ，相对误差为 0 00 ||A A AA −Δ = ．真值 A0 常以公认值、理论值或多次测量的平均值代替． [典型分析] 【例 1】 一打点计时器固定在斜面上某处，一小车拖着穿过打点计器的纸带从斜面上滑下，如图 5-1 甲所示，图 5—1 乙是打出的纸带的一段．　 图 5—1 （1）已知打点计时器使用的交流电频率为 50Hz，利用图乙给出的数据可求出小车下滑的加速度 a=____________． （2）为了求出小车在下滑过程中所受的阻力，还需要测量的物理量有___________，用测得的量及加速度 a 表示阻力的 计算式为 f =_________________．　 【例 2】 一个有一定厚度的圆盘，可以绕通过中心且垂直于盘面的水平轴转动．用下面的方法测量它匀速转动时的角 速度． 实验器材：电磁打点计时器，米尺，纸带，复写纸．　 实验步骤：　 （1）如图 5—3 所示，将电磁打点计时器固定在桌面 上，将纸带的一端穿过打点计时器 的限位孔后，固定在待测圆盘的侧面上，使圆盘转动时， 纸带可以卷在圆盘侧面上．　 （2）启动控制装置使圆盘转动，同时接通电源，打点 计时器开始打点． （3）经过一段时间，停止转动和打点，取下纸带，进 行测量． ①由已知量和测得量表示角速度的表达式为ω=________________，式中各量的意义是___________． ②某次实验测得圆盘半径 r =5.50×10－2m，得到的纸带的一段如图 5—4 所示，求得角速度为________． 图 5—4 【例 3】 小灯泡灯丝的电阻会随温度的升高而变大．某同学为研究这一现象，用实验得到如下数据（I 和 U 分别表示 图 5—3 单位：cm 小灯泡上的电流和电压）：　 I/(A) 0.12 0.21 0.29 0.34 0.38 0.42 0.45 0.47 0.49 0.50 U(V) 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60 1.80 2.00 （1）在左下框中画出实验电路图．可用的器材有：电压表、电流表、滑线变阻器（变化范围 0～10Ω）、电源、小灯 泡、电键、导线若于．　 （2）在图 5—5 中画出小灯泡的 U—I 曲线． 图 5—5 （3）若将该小灯泡接在电动势是 1.5V，内阻是 2.0Ω的电池两端，小灯泡的实际功率是多少?（简要写出求解过程，若 需作图，可直接画在图中） 三、实验设计 [专题精讲] 实验设计应把重点放在力学和电学实验上，力学以打点计时器为中心展开，电学以电阻测量为中心展开．　 1．进行实验设计的总体原则　 （1）精确性：在实验误差允许的范围内，应尽可能选择误差较小的方案．　 （2）安全性：实验方案的实施要安全可靠，不会对器材造成损害，且成功率高．　 （3）可操作性：实验应便于操作和读数，便于进行数据处理．　 2．实验设计的基本思路　 →→ →→ ⎧⎪⎨ ⎪⎩ 实验器材 明确目的 确定原理 待测物理量 数据处理 误差分析 实验步骤 ． 实验设计的关键在于实验原理的设计，它是进行实验的依据和起点，它决定了应选用（或还需）哪些实验器材，应测量 哪些物理量，如何编排实验步骤．而实验原理的设计又往往依赖于所提供的实验器材（条件）和实验要求，它们相辅相成， 互为条件．　 以测量电表的内阻为例： 纵向：伏安法及变式 1°电流表、电压表各一只，可以测量它们的内阻 V A V A 2°两只同种电表，若知道一只的内阻，就可以测另一只的内阻 3°两只同种电表内阻都未知，则需要一只电阻箱才能测定电表的内阻 横向：除伏安法外，还常用替代法、半偏法和闭合电路欧姆定律（计算法） 1°替代法 2°半偏法 3°闭合电路欧姆定律（计算法） 3．电学实验的器材选择和电路设计　 （1）电路结构　 完整的实验电路包括三个部分：①测量电路，②控制电路（变阻器、开关），③电源． （2）思路　 A2 A1 V1 V2 R A1 A2 V2 V1 R G R2 S2 R1 S1 R1 S V R2 G2 G2 R 2 1 V1 V2 R 2 1 S S V S 2 R E r （电阻不 1 测量电路 器材选择 配置 控制电路 电路选择 控制 调节 （3）方法　 ①电表选择：为了减小电表读数引起的偶然误差，选择电表时应先估算待测电流或电压的最大值，同时要考虑电表间、 电表与电源间的配置是否合理，测量时各电表的最大偏转量都应接近量程．　 ②分压、限流电路选择　 在下列情况下应选择分压电路　 1°实验要求待测电阻两端电压从零开始连续变化。　 2°限流不能保证安全，即限流电路中的最小电流超过电表量程或用电器的额定电流．常见于变阻器全电阻远小于测量 部分电阻的情况．　 3°限流能保证安全，但变阻器调节过程中，电表读数变化不明显，不满足实验测量多组数据的要求．常见于变阻器全 电阻远小于测量部分电阻的情况．　 在限流、分压两种电路都满足实验要求时，由于限流电路结构简单，损耗的电功率小，应优先选用．　 ③滑动变阻器的粗调和微调．　 在限流电路中，对测量电路而言，全电阻较大的变阻器起粗调作用，全电阻较小的变阻器起微调作用；在分压电路中， 变阻器的粗、微调作用正好与限流电路相反．　 [典型分析] 【例 4】 如图 5—8 所示，水平桌面上固定着斜面 体 A，有小铁块 B．斜面体的斜面是 曲面，由其截面图可以看出曲线下端的切线是水平 的．现提供的实验测量工具有：天 平、直尺． 其它的实验器材可根据实验需要自选．现 要设计一个实验，测出小铁块 B 自 斜面顶端由静止下滑到底端的过程中，小铁块 B 克服摩 擦力做的功．请回答下列问题：　 （1）除题中供给的器材处，还需要选用的器材是： ____________________________________________________________． （2）简要说明实验中需要测量的物理量(要求在图上标明)： _____________________________________________________________． （3）写出实验结果的表达式（重力加速度 g 已知）： ____________________________________________________________． 【例 5】 用伏安法测量一个定值电阻的阻值，备用器材如下 ：　 待测电阻 Rx （阻值约为 25kΩ） 电流表 A1：（量程 100 μ A，内阻 2kΩ） 电流表 A2：（量程 500 μ A，内阻 300Ω） 电压表 V1：（量程 10V，内阻 100kΩ） 电流表 V2：（量程 50V，内阻 500kΩ） 电源 E：（电动势 15V，允许最大电流 1A） 滑动变阻器 R：（最大阻值 1kΩ） 电键 S，导线若干　 为了尽量减小实验误差，要求测多组数据．　 （1）电流表应选________________，电压表应选__________________．　 （2）画出实验电路图．　 图 5—8 【变式】 用以下器材测量一待测电阻 Rx 的阻值（900～1000Ω）：　 电源 E，具有一定内阻，电动势约为 9.0V； 电压表 V1，量程为 1.5V，内阻 r1=750Ω；　 电压表 V2，量程为 5V，内阻 r2=2500Ω；　 滑线变阻器 R，最大阻值约为 100Ω； 单刀单掷开关 S，导线若干． （1）测量中要求电压表的读数不小于其量程 的 1 3 ，试画出测量电阻 Rx 的一种实 验电路原理图(原理图中的元件要用题图中的相应 的英文字母标注）．　 （2）根据你所画的电路原理图在题给的实物图 5—11 上画出连线．　 （3）若电压表 V1 的读数用 U1 表示，电压表 v2 的读数用 U2 表示，则由已知量和 测得量表示 Rx 的公式为 Rx=____________________．　 【例 6】 为了测定电流表 A1 的内阻，采用如 图 5—14 所示的电路．其中：A1 是 待测电流表，量程为 300 μ A，内阻约为 100Ω； A2 是标准电流表，量程为 200 μ A； R1 是电阻箱，阻值范围是 0～999.9Ω；R2 是滑动变 阻器；R3 是保护电阻；E 是电池组， 电动势为 4V，内阻不计；S1 是单刀掷开关．S2 是单刀双掷开关．　 图 5—14 图 5—15 （1）根据电路图，请在图 5—15 中画出连线，将器材连接成实验电路．　 （2）连接好电路，将开关 S2 扳到接点 a 处，接通开关 S1，调整滑动变阻器 R2 使电表 A2 的读数是 150 μ A；然后将开关 S2 扳到接点 b 处，保护 R2 不变， 调节电阻 R1，使 A2 的读数仍为 150 μ A．若 此 时电阻箱各旋钮的位置如图 5—16 所示，电阻箱的阻值是_______Ω，则待测电流 表 A1 的内阻 R1=______Ω． （3）上述实验中，无论怎样调整滑动变阻 器 R2 的滑动端位置，都要保证两 块电流表的安全．在下面提供的四个电阻中， 保护电阻 R3 应选用： _____________________（填写阻值相应的字 母）． 　 A ． 200k Ω B． 20k Ω C．15kΩ D．20Ω （4）下面提供最大阻值不同的四个滑动变 阻器供选用．既要满足上述实验要 求，又要调整方便，滑动变阻器 ___________________（填写阻值 相应的字母）是最佳选择．　 　 A．1kΩ B．5kΩ C．10kΩ D．25kΩ　　 【例 7】 现有一块 59C2 型的小量程电流表 G（表头），满偏电流为 50 Aμ ，内阻约为 800～850Ω，把它改装成 1mA、 10mA 的两量程电流表，可供选择的器材有：　 滑动变阻器 R1，最大阻值 20Ω；滑动变阻器 R2，最大阻值 100kΩ；　 电阻箱 R′，最大阻值 9999Ω；定值电阻 R0，阻值 1kΩ；　 图 5—11 图 5—16 电池 E1，电动势 1.5V；电池 E2，电动势 3V；电池 E3，电动势 4.5V；（所有电池内阻不计），标准电流表 A，满偏电 流 1.5mA； 单刀单掷开关 S1 和 S2；单刀双掷开关 S3；电阻丝及导线若干．　 （1）采用如图 5—18（甲）所示电路测量表头的内阻，为提高测量精确度，选用的滑动变阻器为____ ______________，选用的电池为_______________．　 甲 乙 丙 图 5—18 （2）将 G 改装成两量程电流表，现有两种备选电路，如图 5—18（乙）、（丙）所示．图_________为合理电路，另一 电路不合理的理由是_______________________________． （3）将改装后的电流表与标准电流表逐格进行核对（仅核对 1mA 量程），画出所用电路图，图中待核对的电流表符号 用 A′ 来表示．　 【例 8】 （1）一个电压表 VA 的内阻 RA=1000Ω， 量程为 1.0V，现要利用电阻箱扩大 它的量程，改装成量程为 3.0V 的电压表．改装后，再用 一量程为 3.0V 的精确的电压表 VB 对改装后的电压表的所有刻度进行校准．除了这两个电 压表 VA、VB 外，还有下列一些器材： 　 电源 E（电动势约为 6V，内阻较小） 变阻器 R（总电阻约 10Ω） 电阻箱 R0（0～9999Ω） 开关 S 导线若干 ①如图 5—20 所示是以上器材和两个电压表 VA、 VB 的实物示意图，试在图中画出连 线，连成进行校准时的实验电路． ②图中电阻箱的取值等于________________Ω．　 （2）用上述电压表 VB 和改装后并已校准过的电压表（以下称之为 VC）以及一个开关和一些导线，去测量一个电动势 大约为 2V 的电源的内阻 r． ①简要写出测量步骤．　 ②用测得的量表达 r 的公式应为 r=____________．　 图 5—20 四、跟踪练习 1．下列关于误差的说法正确的是(填字母)____________． 　 A．误差是实验中产生的错误 B．误差都是由于测量不仔细产生的　 C．误差都是由于测量工具不精密产生的 D．任何测量都存在误差　 E．实验时认真测量就可以避免误差 F．采用精密仪器，改进实验方法，可以消除误差　 G．实验中产生误差是难免的，但可以想办法尽量减小误差　 H．多次测量取平均值可以减小偶然误差 I．多次测量取平均值可以减小系统误差 2．甲、乙、丙三位同学在使用不同的游标卡尺测量同一物体的长度时，测量的结果分别如下：　 甲同学：使用游标为 50 分度的卡尺，读数为 12.045cm 乙同学：使用游标为 10 分度的卡尺，读数为 12.04cm 丙同学：使用游标为 20 分度的卡尺，读数为 12.045cm 从这些数据中可以看出读数肯定有错误的是____________同学． 3．如图 5—22 甲、乙所示，用同一套器材测量铁块 P 与长金属板间的滑动摩擦力．甲图使金属板静止在水平桌面上，用手 通过弹簧秤向右用力 F 拉 P，使 P 向右运动；乙图把弹簧秤的一端固定在墙上，用力 F 水平向左拉金属板，使金属板向 左运动．则铁块 P 与金属板间的滑动摩擦力的大小是__________N． 图 5—22 图 5—23 4．在“研究平抛物体的运动”的实验中，得到的轨迹如图 5—23 所示．根据平抛运动的规律及图中给出的数据，可计算出 小球平抛的初速度 v0=________m/s． 5．在验证机械能守恒定律的实验中，质量 m=1kg 的重物自由下落，在纸带上打出了一系列的点，如图 5—24 所示，相邻记 数点间的时间间隔为 0.02s，长度单位是 cm，g 取 9.8m/s2．求： 图 5—24 （1）打点计时器打下计数点 B 时，物体的速度 vB=________________(保留两位有效数字)．　 （2）从起点 O 到打下记数点 B 的过程中，物体重力势能减小量ΔEP=___________，动能的增加量ΔE- k=_________________（保留两个有效数字）．　 （3）即使在实验操作规范、数据测量及数据处理很准确的前提下，该实验求得的ΔEp 也一定略大一 ΔEk，这是实验存在系统误差的必然结果，试分析该系统误差产生的主要原因． 6．在测定一节干电池（电动势约为 1.5V，内阻约为 2Ω）的电动势和内阻的实验中，变阻器和电压表各有两个供选： A 电压表量程为 15V，B 电压表量程为 3V，A 变阻器为（20Ω，3A），B 变阻器为（500 　Ω，0.2A）．　 电压表应该选_______________ (填 A 或 B)，这是因为____________________．变阻器应该选_______________ (填 A 或 B)，这是因为__________________________． 7．利用如图 5—25 所示的电路测量电流表 mA 的内阻，闭合电键 S，当变阻器的滑片滑至 c 处时，测得电流表 mA 和 电压表 V 的示数分别是 40mA、9V．已知图 5—25 中热敏电阻的 I—U 关系图线如图 5—26 所示，则电流表 mA 的内阻为（ ） 图 5—25 图 5—26 A．0.14Ω 　 B．85Ω C．140Ω 　 D．225Ω 8．如图 5—27 所示，一只黑箱有 A、B、C 三个接线柱，规定每两个接线柱间最多只能接一个电器元件．并且已知黑箱 内的电器元件是一只电阻和一只二极管．某同学利用多用电表的欧姆挡，用正确的操作方法依次进行了 6 次测量，将每次红、 黑表笔的位置和测得的阻值都填入了下表．　 红表笔接 A A B B C C 黑表笔接 B C A C A B 测得阻值(Ω) 100 10k 100k 10.1k 90 190 由表中的数据可以判定:　 （1）电阻接在_________________两点间，阻值 为_________________Ω． （2）二极管接在_________________两点间，其 中正极接在_________________ 点．二极管的正向阻值为____________Ω，反向阻值 为______________Ω． 9．在“用双缝干涉测光的波长”的实验中，测量 头示意图如图 5—28 所示，调节分 划板的位置，使分划板中心剖线对齐某亮条纹的中心， 此时测量头的读数为 _________________mm，转动手轮，使分划线向一侧 移动，到另一条亮条纹的中心位 置，由测量头再读出一读数．若实验测得第一条到第 五条亮条纹中心间的距离为Δx = 0.960mm，已知双缝间距为 d=1.5mm，双缝到屏的距离为 L=1.00m，则对应的光波波长 λ =_________________nm． 图 5—28 图 5—29 10．如图 5—29 所示，画有直角坐标系 Oxy 的白纸位于水平桌面上．M 是放在白纸上的半圆形玻璃砖，其底面的圆心 在坐标原点，直边与 x 轴重合．OA 是画在纸上的直线，P1、P2 为竖直地插在直线 OA 上的两枚大头针，P3 是竖直地插在纸 图 5—27 上的第三枚大头针，α 是直线 OA 与 y 轴正方向的夹角， β 是直线 OP3 与 y 轴负方向的夹角．只要直线 OA 画得合适，且 P3 的位置取得正确，测出角α 、 β ，便可求得玻璃的折射率．　 某学生在用上述方法测量玻璃的折射率时，在他画出的直线 OA 上竖直地插上了 P1、P2 两枚大头针，但在 y<0 的区域 内，不管眼睛放在何处，都无法透过玻璃砖看到 P1、P2 的像，他应采取的措施是______________________________．若他 已透过玻璃砖看到了 P1、P2 的像，确定 P3 位置的方法是___________________________________．若他已正确地测得了α 、 β 的值，则玻璃的折射率 n=________________． 11．在用“油膜法估测分子大小”的实验中， 所用油酸酒精的浓度为每 104mL 溶 液中有纯油酸 6mL，用注射器测得 1mL 上述溶液 为 75 滴．把 1 滴该溶液滴入盛水的 浅盘里，待水面稳定后，将玻璃板放在浅盘上，用 笔在玻璃板上描出油酸的轮廓形状， 再把玻璃板放在坐标纸上，其形状和尺寸如图 5— 30 所示，坐标中正方形方格的边长 为 1cm．试求： （1）油酸膜的面积是____________cm2． （2）每滴油酸酒精溶液中含有纯油酸的体积是 ______________mL． （3）按以上实验数据估测出油酸分子直径为 ___________m．[（2）、（3）两问 答案取一位有效数字] 12．在一次用单摆测定重力加速度的实验中， 图 5—31（甲）的 O 点是摆线的悬挂 点，a、b 点分别是球的上沿和球心，摆长 L=_____________m．　　 图 5—31 图（乙）为测量周期用的秒表，长针转一圈的时间为 30s，表盘上部的小圆共 15 大格，每一大格 1min，该单摆摆动 n=50 次时，长、短针位置如图所示，所用时间 t=_____________s． 用以上直接测量的物理量的英文符号表示重力加速度的计算式为 g=_____________（不必代入具体数值）． 13．电磁打点计时器是一种计时装置，请根据电磁打点计时器的相关实验回答下列问题（电磁打点计时器所用电源频率 为 50Hz）： （1）如图 5—32 所示，某同学设计了一个用电磁打点计时器验证动量守恒定律的实验装置，在光滑水平面上，小车 A 的前端粘有橡皮泥，小车 A 受到瞬时冲量作用后做匀速运动，与原来静止在前方的小车 B 相碰并粘合成一体，继续做匀速 运动．　 图 5—32 实验得到的打点纸带如图 5—33 所示，小车 A 的质量为 0.4kg，小车 B 的质量为 0.2kg， 则碰前两小车的总动量为__________________kg·m/s，碰后 两小车的总动量为 ___________]kg·m/s．（计算结果保留三位有效数字） 图 5—30 图 5—34 甲 乙 图 5—33 （2）在“验证机械能守恒定律”的实验中：　 ①某同学用图 5—34 所示装置进行实验，得到如图 5—35 所示的纸带．测出点 A、C 间的距离为 14.77cm，点 C、E 间 的距离为 16.33cm，已知当地重力加速度为 9.8m/s2，重锤的质量为 m=1.0kg，则垂锤在下落过程中受到的平均阻力大小 Ff =_____________ 图 5—35 ②某同学上交的实验报告显示重锤的动能略大于重锤的势能，则出现这一问题的原因可能是_______（填序号）．　 　 A．重锤的质量测量错误 　 B．该同学自编了实验数据　 　 C．交流电源的频率不等于 50Hz 　 D．重锤下落时受到的阻力过大 14．如图 5—36 所示，A、B 是两个相同的小物块，C 是轻弹簧，用一根细线连接 A、B 使弹簧 C 处于压缩状态，然后 放置在光滑的水平桌面上．提供的测量器材有天平和刻度尺．试设计一个测定弹簧此时弹性势能 Ep 的实验方案，说明实验 中应测定的物理量(同时用相应的字母表示)，并写出计算弹簧弹性势能 Ep 的表达式（用测得物理量的字母表示）． 图 5—36 15．图 5—37 中 E 为直流电源，R 为已知电阻，V 为理想电压表，其量程略大于电源电动势，S1 和 S2 是开关．现要利 用图中电路测量电源的电动势 E 和内阻 r，试写出主要实验步骤及结果的表达式． 图 5—37 16．在“测定金属的电阻率”的实验中，需要用刻度尺测出被测金属丝的长度 l，用螺旋测微器测出金属丝的直径 d， 用电流表和电压表测出金属丝的电阻 Rx． 图 5—38 图 5—39 （1）请写出测金属丝电阻率的表达式： ρ ＝_________________（用上述测量量的字母表示）． （2）若实验中测量：金属丝的长度和直径时，刻度尺和螺旋测微器的示数分别如图 5—38 所示，则金属丝长度的测量 值为 l＝_________________cm 　，金属丝直径的测量值为 d=_________________mm． （3）用电流表和电压表测金属丝的电阻时，由于电压表、电流表内阻的影响,不论使用电流表内接法还是电流表外接法, 都会产生系统误差．按如图 5—39 所示的电路进行测量,可以消除由于电表内阻造成的系统误差．利用该电路进行实验的主 要操作过程是: 第一步：先将 R2 的滑动头调到最左端,单刀双掷开关 S2 向 1 闭合，闭合电键 S1，调节变阻器 R1 和 R2,使电压表和电流表 的示数尽量大些（不超过量程），读出此时电压表和电流表的示数 U1、I1． 第二步：保持两滑动变阻器的滑动头位置不变，将单刀双掷开关 S2 向 2 闭合，读出此时电压表和电流表的示数 U2、I2．　 请写出由以上记录数据计算被测电阻 Rx 的表达式 Rx=__________________． 17．某研究性学习小组为探究小灯泡灯丝电阻与温度的关系，设计并完成了有关的实验，以下是实验中可供选用的器 材．　 　 A．待测小灯泡（额定功率 6W，额定电流 0.5A） 　 B．电流表（量程 0～0.6A，内阻 0.1Ω） 　 C．电压表（量程 0～5V，内阻约 5kΩ） 　 D．电压表（量程 0～15V，内阻约 15kΩ） 　 E．滑线变阻器（最大阻值 50Ω） 　 F．滑线变阻器（最大阻值 1kΩ） 　 G．直流电源（电动势 15V，内阻可忽略） H．开关一个，导线若干　 实验中调节滑线变阻器，小灯泡两端电压可以从零至额定电压范围内变化，从而测出小灯泡在不同电压下的电流．　 （1）请在虚线框中画出为完成上述实验而设计的合理的电路图．并在每个选用的器材旁标上题目所给的字母序号．　 图 5—40 （2）如图 5—40 所示是该研究小组测得小灯泡的 I—U 关系图线．由图线可知，小灯泡灯丝电阻随温度的升高而 _________________（填“增大”、“减小”或“不变”）；当小灯泡两端所加电压为 6V 时，其灯丝电阻值约为_________________ Ω．（保留两位有效数字） 18．有以下可供选用的器材及导线若干条,要求使用个数最少的仪器尽可能精确地测量一个电流表的满偏电流．　 　 A．被测电流表 A1：满偏电流约 700～800 Aμ ，内阻约 100Ω，刻度均匀、总格数为 N 　 B．电流表 A2：量程 0.6A，内阻 0.1Ω C．电压表 V：量程 3V，内阻 3kΩ　　 　 D．滑动变阻器 R1：最大阻值 200Ω 　 E．滑动变阻器 R2：最大阻值 1kΩ　　 　 F．电源 E：电动势 3V、内阻 1.5Ω 　 G．开关一个 （1）在虚线框内画出实验电路图,并在每个选用的仪器旁标上题目所给的字母序号． （2）测量过程中测出多组数据,其中一组数据中待测电流表 A 的指针偏转了 n 格，可算出满偏电流 Ig=___________，式 中除 N、n 外,其他字母符号代表的物理量是______________． 19．实验室中现有的器材如下：　 电池 E （电动势约 10V、内阻 r 约 1Ω） 标准电流表 A1（量程 300mA，内阻 r1 约为 5Ω） 电阻箱 R1（最大阻值 999.9Ω，阻值最小改变量为 0.1Ω） 滑动变阻器 R2（最大阻值 10Ω） 开关 S 和导线若干．　 要求设计—个测定电流表 A2（量程 250mA，内阻 r2 约为 5Ω）内阻的实验方案．　 （1）在方框中画出测量电路，并在每个仪器旁标上英文代号．　 （2）要直接测出的物理量是____________________，用这些物理量表示待测电流表 A2 内阻的计算公式是 ______________． 20．如图 5—41 中给出的器材为：　 电源 E（电动势为 12V，内阻不计）； 木板 N（板上从下往上依次叠放白纸、复写 纸、导电纸各一张）； 两个金属条 A、B（平行放置在导电纸上，与 导电纸接触良好，用作电极）；　 滑线变阻器 R（其总电阻值小于两平行电极 间导电纸的电阻）；　 直流电压表○V （量程为 6V，内阻很大，其 负接线柱与 B 极相连，正接线柱与 探针 P 相连）； 开关 S．　 现要用图中仪器描绘两平行金属条 AB 间电场中的等势线．AB 间的电压要求取为 6V．　 （1）在图中连线，画成实验电路原理图．　 （2）下面是重要的实验操作步骤，将所缺的内容填写在横线上方．　 图 5—41 a．接好实验电路．　 b．____________________________________________．　 c．合上 S，并将探针 P 与 A 相接触．　 d．____________________________________________．　 e．用探针压印的方法把 A、B 的位置标记在白纸上，画一线段连接 AB 两极，在连线上选取间距大致相等的 5 个点作为 基准点，用探针把它们的位置压印在白纸上．　 f．将探针与某一基准点相接触，________________________，这一点是此基准点的等势点．用探针把这一点的位置也 压印在白纸上．用相同的方法找出此基准点的其他等势点．　 g．重复步骤 f，找出其他 4 个基准点的等势点，取出白纸画出各条等势线． 21．在测定一节干电池的电动势和内阻的实验中，备有下列器材：　 　 A．干电池 E（电动势约为 1.5V，内阻小于 1.0Ω） B．电流表 A1（满偏电流 3mA，内阻 r1=10Ω） C．电流表 A2（0～0.6A，内阻 0.1Ω） D．滑线变阻器 R1（0～20Ω，10A）　 E．滑线变阻器 R2（0～100Ω，10A） F．定值电阻 R3（990Ω）　 G．开关和导线若干　 （1）为方便且能较准确地进行测量，其中应选用的滑线变阻器是______________（填字母代号）　 （2）请在虚线框内画出利用本题提供的器材所设计的测量电池电动势和内阻的实验电路图．　 图 5—42 （3）如图 5—42 为某一同学根据他所设计的实验给出的 I1、I2 图线（I1 为 A1 的示数，I2 为 A2 的示数），由图线可求得 被测电池的电动势 E＝______________V，内阻 r =_____________Ω． 22．实验室内有一电压表○mA ，量程为 150mV，内阻约为 150Ω．现要将其改成量程为 10 mA 的电流表，并进行校准．为 此，实验室提供如下器材：干电池 E（电动势为 1.5V），电阻箱 R，滑线变阻器 R′，电流表○A （有 1.5mA，15mA 与 150 mA 三个量程）及开关 S．　 （1）对电表改装时必须知道电压表的内阻．可用如图 5—43 所示的电路测量电压表○mA 的内阻．在既不损坏仪器又能 使精确度尽可能高的条件下，电路中的电流表○A 应选用的量程是________________．若合上 S，调节滑线变阻器后测得电 压表的读数为 150mV，电流表○A 的读数为 1.05 mA，则电压表的内阻 RmV 为______________．(取三位有效数字)　 图 5—43 （2）在对改装成的电流表进行校准时，把○A 作为标准电流表，画出对改装成的电流表进行校准的电路原理图（滑线变 阻器作限流使用），图中各元件要用题中给出符号或字母标注．图中电阻箱的取值是_______（取三位有效数字），电流表○A 应选用的量程是_____________________． 23．一只量程为 1V，内阻 RV 约为 900Ω的电压表是由小量程电流表改装而成的，现在要测量它的内阻并对该表进行校 正．实验室提供了以下供选择的器材：　 　 A．待测电压表 B．标准电压表（量程 1 V） C．滑动变阻器（最大阻值 1 000Ω，额定电流 1A） D．滑动变阻器（最大阻值 10Ω，额定电流 1A） E．电阻箱（最大阻值 999．9Ω，最小改变量 0.1Ω） F．电阻箱（最大阻值 99．9Ω，最小改变量 0.1 Ω） G．电池组（电动势约 3 V，内阻约 1Ω） H．导线和开关若干．　 （1）为了用半偏法测量该电压表的内阻，某同学设计了两种电路，如图 5—44 甲、乙所示，要使测量较精确，应选择 ___________________（填“甲”或“乙”）电路．在器材的选择上，除了电池组、导线、开关和待测电压表外，还应从提 供的器材中选用___________________________________（用器材前的序号字母表示）．　 用上述方法测出的电压表内阻的测量值 RV_________（填“大于”、“等于”或“小于”）电压表内阻的真实值． 图 5—44 图 5—45 （2）在对该电压表进行校正时，该同学已经选择好器材，如图 5—45 所示．若要求对电压表的每一条刻度线都进行校 正，请你将这些器材连接成测量电路，并标出所选滑动变阻器的序号字母． 24．量程为 3V 的电压表 V 内阻约为 3kΩ，要求测出该电压表内阻的精确值．实验中可供选用的器材有：　 电阻箱 Ra（最大值 9999.9Ω，阻值最小改变量 0.1Ω）　 滑线变阻器 Rb（最大阻值 1000Ω，允许最大电流 0.2A）　 电源 E（开路电压约为 5V，内阻可忽略不计）　 开关 S 及导线若干　 （1）设计一个易于操作的测量电路，要求画出实验电路图并标出所用器材符号．　 （2）列出测量步骤，并写出计算电压表内阻的最后公式． 专题一 运动和力参考答案 典型例题 [例 1] 解析：对系统进行整体分析，受力分析如图 1 —2： 由平衡条件有： cos30Ff°= sin 30 ( )NF Mmg+°=+ 由此解得 15 3Nf = ()sin30135NNMmgF=+ − °= [例 2] 解析： （1）设 t1、t2 为声源 S 发出两个信 号的时刻， 12、tt′′为观察者接收到 两个信号的时刻．则第一个信号经过 11()tt′ − 时间被观察者 A 接收到，第二个信号经过（ 22tt′ − ）时刻被观察者 A 接收到， 且 21 21tt t t t t′′′Δ= − Δ = − f N F (M＋m)g 图 1—2 t1 vA S A t1 1t′ A L 11()Avt t′ − t1 vA S A t1 2t′ A L 21()Avt t′ − 22()Pvt t′ − t2 vS SvtΔ 设声源发出第一个信号时，S、A 两点间的距离为 L，两个声信号从声源传播到观察者的过程中，它们的运动的距离关系 如图所示， 可得 11 11 2 2 21() () ( ) ()PAPASvt t Lvt t vt t Lvt t v t′′′′−=+ − − =+ −−Δ 由以上各式解得 PS PA vvttvv −′Δ= Δ− （2）设声源发出声波的振动周期为 T，这样，由以上结论，观察者接收到的声波振动的周期 T′, PS PA vvTTvv −′ = − ． 由此可得，观察者接收到的声波频率与声源发出声波频率间的关系为 PA PS vvf fvv −′ = − ． [例 3] 解答：根据题意作图 1—4． 对这两个天体而言，它们的运动方程分别为 212 112 mmGmr r ω= ① 212 222 mmGmr r ω= ② 以及 12rr r+= ③ 由以上三式解得 21 12 12 12 ;mmrrrrmm mm==++ ． 将 r1 和 r2 的表达式分别代①和②式， 可得 12()1 Gm m rrω += ． 212 11 2 12 12 112 22 1 12 12 12 () () () () 2 2 () mGmm Gvr mmm r mmr mGmm Gvr mmm r mmr rTrGm m ω ω π πω +== =++ +== =++ == + [例 4] 解答：（1）A、B 两球以相同的初速度 v0，从同一点水平抛出，可以肯定它们沿同一轨道运动． 作细线刚被拉直时刻 A、B 球位置示意图 1—5． 根据题意可知： 0 22 2 2 4.5 0.8 3.6(m) 63.64.8(m) xvt yl x Δ= Δ= × = Δ= −Δ= − = 设 A 球运动时间为 t，则 B 球运动时间为 t－ 0.8，由于 A、B 球在竖直方向上均作自 由落体运动，所以有 2211(0.8)22ygtgtΔ= − − ． 由此解得 t =1s． （2）细线刚被拉直时， A、B 球的水平位移分别为 004.5m ( 0.8) 0.9mABxvt xvt== = − = [例 5] 解答：（1）A 球通过最低点时，作用于环形圆管的压力竖直向下，根据牛顿第三定律，A 球受到竖直向上的支 11()Pvt t′ − r2 r1 mm O 图 1—4 x y 图 1—5 持力 N1，由牛顿第二定律，有： 2 0 11 1 vNmgmg−= ① 由题意知，A 球通过最低点时，B 球恰好通过最高点，而且该时刻 A、B 两球作用于圆管的合力为零；可见 B 球作用于 圆管的压力肯定竖直向上，根据牛顿第三定律，圆管对 B 球的反作用力 N2 竖直向下；假设 B 球通过最高点时的速度为 v， 则 B 球在该时刻的运动方程为 2 22 2 vNmgmR+= ② 由题意 N1=N2 ③ ∴ 22 102 12 mvmvmg m g RR+= − ④ 对 B 球运用机械能守恒定律 22 20 2 2 11222mv mv mgR=+ ⑤ 解得 22 0 4vv gR=− ⑥ ⑥式代入④式可得： 2 0 12 12(5)( ) 0vmmgmmR++−=． [例 6] 解答：火箭上升到最高点的运动分为两个阶段：匀加速上升阶段和竖直上抛阶段． 地面上的摆钟对两个阶段的计时为 1 2 2 64000 40(s)810 ht a ×== =× 1 218 320(s)atttg=== 即总的读数（计时）为 t =t1＋t2=360（s） 放在火箭中的摆钟也分两个阶段计时． 第一阶段匀加速上升，a=8g，钟摆周期 112233 llTTga gππ′ ===+ 其钟面指示时间 113120stt′ == 第二阶段竖直上抛，为匀减速直线运动，加速度竖直向下，a=g，完全失重，摆钟不“走”，计时 2 0t′ = ．可见放在火 箭中的摆钟总计时为 12120sttt′′′=+ = ． 综上所述，火箭中的摆钟比地面上的摆钟读数少了 240sttt′Δ =− = ． [例 7] 解答：在情形（1）中，滑块相对于桌面以速度 v0=0.1m/s 向右做匀速运动，放手后，木板由静止开始向右做 匀加速运动． 20.02m/smga M μ== 经时间 t，木板的速度增大到 v0=0.1m/s， 0 5svt a= = ． 在 5s 内滑块相对于桌面向右的位移大小为 S1=v0t=0.5m． 而木板向右相对于桌面的位移为 2 2 1 0.25m2Sat== ． 可见，滑块在木板上向右只滑行了 S1－S2=0.25m，即达到相对静止状态，随后，它们一起以共同速度 v0 向右做匀速直 线运动．只要线足够长，桌上的柱子不阻挡它们运动，滑块就到不了木板的右端． 在情形（2）中，滑块与木板组成一个系统，放手后滑块相树于木板的速度仍为 v0，滑块到达木板右端历时 0 5slt v ′ = = ． [例 8] 解答：以 m 表示球的质量，F 表示两球相互作用的恒定斥力，l 表示两球间的原始距离．A 球作初速度为 v0 的 匀减速运动，B 球作初速度为零的匀加速运动．在两球间距由 l 先减小，到又恢复到 l 的过程中，A 球的运动路程为 l1，B 球运动路程为 l2，间距恢复到 l 时，A 球速度为 v1，B 球速度为 v2． 由动量守恒，有 012mv mv mv=+ 由功能关系：A 球 22 101 11 22Flmvmv=− B球： 2 22 1 2Flmv= 根据题意可知 l1=l2， 由上三式可得 222 222 2 012 02 20 022() 22vvv vv vv vvv=+= − +=− + 得 v2=v0、v1=0 即两球交换速度． 当两球速度相同时，两球间距最小，设两球速度相等时的速度为 v， 则 0 0 (),2 vmv m m v v=+ = B 球的速度由 0 2 vv = 增加到 v0 花时间 t0，即 0 00 02 vvvat at=+ = + 得 0 02 va t= ． 解二：用牛顿第二定律和运动学公式．（略） 跟踪练习 1．C 提示：利用平衡条件． 2．（1）重物先向下做加速运动，后做减速运动，当重物速度为零时，下降的距离最大，设下降的最大距离为 h， 由机械能守恒定律得 222 ( ( sin ) sin )Mgh mg h R Rθ θ=+− 解得 2hR= ． （2）系统处于平衡状态时，两小环的可能位置为 a．两小环同时位于大圆环的底端 b．两小环同时位于大圆环的顶端 c．两小环一个位于大圆环的顶端，另一个位于大圆环 的底端 d．除上述三种情况外，根据对称性可知，系统如能平 衡，则小圆环的位置一定关于大 圆环竖直对称轴对称．设平衡时，两小圆环在大圆环竖直对 称轴两侧α 角的位置上（如图）． 对于重物 m，受绳的拉力 T 与重力 mg 作用，有 T=mg．对 于小圆环，受到三个力的作用， 水平绳的拉力 T，竖直绳的拉力 T，大圆环的支持力 N．两 绳的拉力沿大圆环切向的分力大 小相等，方向相反 sin sinTTα α′= ． 得 ,90,45α ααα α′′=+=°=°而∴． 3．设测速仪扫描速度为 v′，因 P1、P2 在标尺上对应 间 隔 为 30 小格，所以 30 30v t ′ ==Δ 格/s． 测速仪发出超声波信号 P1 到接收 P1 的反射信号 n1．从图 B 上可以看出，测速仪扫描 12 小格，所以测速仪从发出信号 P1 到接收其反射信号 n1 所经历时间 12 0.4st v ′ ==′ ． 汽车接收到 P1 信号时与测速仪相距 1 1 68m2 tSv==声 ． 同理，测速仪从发出信号 P2 到接收到其反射信号 n2，测速仪扫描 9 小格，故所经历时间 2 9 0.3st v==′ ．汽车在接收到 T α′ α N α m m mg T P2 信号时与测速仪相距 2 2 51m2 tSv==声 ． 所以，汽车在接收到 P1、P2 两个信号的时间内前进的距离△S=S1－S2=17m． 从图 B 可以看出，n1 与 P2 之间有 18 小格，所以，测速仪从接收反射信号 n1 到超声信号 P2 的时间间隔 3 18 0.6st v==′ ． 所以汽车接收 P1、P2 两个信号之间的时间间隔为 12 3 0.95s22 ttttΔ= + + = ． ∴汽车速度 17.9Sv t Δ==Δ m/s． 4．从 B 发出第一个超声波开始计时，经 2 T 被 C 车接收．故 C 车第一次接收超声波时与 B 距离 102 TSv= ． 第二个超声波从发出至接收，经 T＋△T 时间，C 车第二车接收超声波时距 B 为 202 TTSv+Δ= ，C 车从接收第一个超 声波到接收第二个超声波内前进 S2－S1，接收第一个超声波时刻 1 2 Tt = ，接收第二个超声波时刻为 20 2 TTtT +Δ=+ ． 所以接收第一和第二个超声波的时间间距为 21 0 2 Ttt t T ΔΔ= − = + ． 故车速 0 021 0 0 2 2 2 2 C vT TvSSv TTtTT Δ Δ−== =+ΔΔ+Δ ．车向右运动． 5．ACD 6．（1）根据动能定理，可求出卫星由近地点到远地点运动过程中，地球引力对卫星的功为 22 21 11 22Wmvmv=−． （2）由牛顿第二定律知 1222 11 2() () GM GMaa Rh Rh == ++ ∴ 21 21 2 ()RhaaRh += + 7．（1）建立如图所示坐标系，将 v0 与 g 进行正交 分解． 0000cos , sin sin , cos xy xy vv vv gg g g θ θ θ θ == ==− 在 x 方向，小球以 0xv 为初速度作匀加速运动． 在 y 方向，小球以 0yv 为初速度，作类竖直上抛运动． 当 y 方向的速度为零时，小球离斜面最远，由运动学公式 0 2 22 0 sin |2 | 2 cos y y v vH gg θ θ== ． 小球经时间 t 上升到最大高度，由 0yyvgt= 得 0 00sin tancos g y v vvt gg g θ θθ== = ． （2） 0 2 2 2 00 0022 1 sin 1 sin2(2)2cos sin42cos2cosAB x x vvSvtgtv vg g θ θθθθ θ =+ = + y yg xg g 0v O x 2 202sin(1 tan )v g θ θ=+ 8 ．（ 1 ）设滑雪者质量为 m ，斜面与水平面夹角为θ ，滑雪者滑行过程中克服摩擦力做功 cos ( cos )W mg S mg L S mgLμ θ μ θ μ=+−= ① 由动能定理 21() 2mg H h mgL mvμ−− = ② 离开 B 点时的速度 2( )vgHhLμ=−− ③ （2）设滑雪者离开 B 点后落在台阶上 2 111 1 222 h gtSvth==< 可解得 1 2( )ShHhLμ=−− ④ 此时必须满足 2H Lhμ− < ⑤ 当 2H Lhμ−>时，滑雪者直接落到地面上， 2 22 22 1 ,2hgtSvt==， 可解得 2 2( )ShHhLμ=−−． 9．AC 10．摆球先后以正方形的顶点为圆心，半径分别为 R1=4a，R2=3a，R3=2a，R4=a 为半径各作四分之一圆周的圆运动． 当摆球从 P 点开始，沿半径 R1=4a 运动到最低点时的速度 v1， 根据动量定理 22 10 11422mv mv mga−= ① 当摆球开始以 v1 绕 B 点以半径 R2=3a 作圆周运动时，摆线拉力最大，为 Tmax=7mg，这时摆球的运动方程为 2 1 max 3 mvTmga−= ② 由此求得 v0 的最大许可值为 0 10vga≤ ． 当摆球绕 C 点以半径 R3=2a 运动到最高点时，为确保沿圆周运动， 到达最高点时的速度 332vgRga=≥ （重力作向心力） 由动能定理 22 2 30 03 11 2422mv mv mga v v ga ga−=− =+得≥ ∴ 0410gav ga≤≤ 11．B 12．由题意知，周期为 42s63T == ．波速 40 3 20m/s2 3 v T λ== = ． P、Q 两点距离相差 9(6 )4− 次全振动所需时间即 92 35(6 ) 4 s.43 22tΔ= − × = − = ∴ 50mPQ v t=Δ= ． 13．ABC 开始时小车上的物体受弹簧水平向右的拉力为 6N，水平向左的静摩擦力也为 6N，合力为零．沿水平向右方 向对小车施加以作用力，小车向右做加速运动时，车上的物体沿水平向右方向上的合力（F=ma）逐渐增大到 8N 后恒定．在 此过程中向左的静摩擦力先减小，改变方向后逐渐增大到（向右的）2N 而保持恒定；弹簧的拉力（大小、方向）始终没有 变，物体与小车保持相对静止，小车上的物体不受摩擦力作用时，向右的加速度由弹簧的拉力提供： 26 0.75m/s8 Ta m=== ． 14．（1）设物体与板的位移分别为 S 物、S 板，则由题意有 2 LSS− =物板 ① 21 2SS vtat=物板 板∶∶ ② 解得： , 2 LSLS= =物板． （2）由 2 2 1 12, ,mg MvvaSa M mgL μ μ===板板 板 得 ． 2 12 ,21,,2, () ,2 S S LS S S LS L mg M m g Ma v a Sμμ ′′ ′′ ′ ′−= = = = ′′′−+= = 物板 物板 板 物 板板板 ∶∶得 由 得 2 2 2( ) Mv M mgLμ = + ，故板与桌面之间的动摩擦因数 2 2 2( ) Mv M mgLμ + ≥ ． 15．在 0～10s 内，物体的加速度 2 1 0.8m/sva t Δ==Δ （正向） 在 10～14s 内，物体的加速度 2 2 2m/sva t Δ==Δ （反向） 由牛顿第二定律 1F mg maμ−= ① 23 F mg maμ−=− ② 由此解得 F=8.4N μ =0.34 16．（1）依题意得 1Bv =0，设小滑块在水平面上运动的加速度大小为 a， 由牛顿第二定律， f mg maμ==，由运动学公式 2 0 2vgSμ= ，解得 0.09μ = ． （2）滑块在水平面上运动时间为 t1，由 0 11 10,3.3s23 vStt===得 ． 在斜面上运动的时间 212 2 0.8s 4.1ssin httttg θ== =+=∴ （3）若滑块在 A 点速度为 v1=5m/s，则运动到 B 点的速度 2 1 24m/sBvvaS=−= ． 即运动到 B 点后，小滑块将做平抛运动． 假设小滑块不会落到斜面上，则经过 3 2 0.4sht g==落到水平面上， 则水平位移 3 1.67m tan 30B hxvt== > ° ． 所以假设正确，即小滑块从 A 点运动到地面所需时间为 3 1 2 1.5s B Sttvv ′ =+ =+ ． 专题二 动量与机械能 典型例题 [例 1] D 解析：本题辨析一对平衡力和一对作用力和反作用力的功、冲量．因为，一对平衡力大小相等、方向相反，作用在同 一物体上，所以，同一段时间内，它们的冲量大小相等、方向相反，故不是相同的冲量，则①错误．如果在同一段时间内， 一对平衡力做功，要么均为零（静止），要么大小相等符号相反（正功与负功），故②正确．至于一对作用力与反作用力，虽 然两者大小相等，方向相反，但分别作用在两个不同物体上（对方物体），所以，即使在同样时间内，力的作用点的位移不 是一定相等的（子弹穿木块中的一对摩擦力），则做功大小不一定相等．而且作功的正负号也不一定相反（点电荷间相互作 用力、磁体间相互作用力的做功，都是同时做正功，或同时做负功．）因此③错误，④正确．综上所述，选项 D 正确． 【例 2】 解析：（1）飞机达到最大速度时牵引力 F 与其所受阻力 f 大小相等， 由 P=Fv 得 m m PPfvfv== （2）航空母舰上飞机跑道的最小长度为 s，由动能定理得 22 0 22 mmv mvPt fs−= − 22 0()22 mmv mvPt s f +− = 将 m Pf v= 代入上式得 22 0()22 m m mv mvPt v s P +− = 或 22 0()[]2 m m mv vs tvP −=+ 【例 3】 解析：解法 1（程序法）： 选物体为研究对象，在 t1 时间内其受力情况如图①所示，选 F 的方向为正方向，根据牛顿第二定律，物体运动的加速 度为 22 1 80.2210m/s 2m/s2 Fmga m μ−−××== =． 撤去 F 时物体的速度为 v1=a1t1=2×6m/s=12m/s 撤去 F 后，物体做匀减速运动，其受力情况如图②所示，根据牛顿第二定律，其运动的加速度为 22 2 0.2 10m/s 2m/smgagm μ μ−==−=−×=−． 物体开始碰撞时的速度为 v2=v1＋a2t2=[12＋(－2)×2]m/s=8m/s． 再研究物体碰撞的过程，设竖直墙对物体的平均作用力为 F ，其方向水平向左．若选水平向左为正方向，根据动量定 理有 32()Ftmvmv′=−−． 解得 12 3 ()2(68)N 280N0.1 mv vF t ′ + ×+== =． 解法 2（全程考虑）：取从物体开始运动到碰撞后反向弹回的全过程应用动量定理，并取 F 的方向为正方向，则 1123()F tmgttFtmvμ ′−+−=− 所以 112 3 () 86(0.2)210(62)26 280N0.1 Ft mg t t mvF t μ ′−++××−×××++×== = NFμ mg F NF ① NFμ mg NF ② 点评：比较上述两种方法看出，当物体所受各力的作用时间不相同且间断作用时，应用动量定理解题对全程列式较简 单，这时定理中的合外力的冲量可理解为整个运动过程中各力冲量的矢量和．此题应用牛顿第二定律和运动学公式较繁琐． 另外有些变力作用或曲线运动的题目用牛顿定律难以解决，应用动量定理解决可化难为易． 【例 4】 解析：该题用守恒观点和转化观点分别解答如下： 解法一：（守恒观点）选小球为研究对象，设小球沿半径为 R 的轨道做匀速圆周运动的线速度为 v0，根据牛顿第二定律 有 2 0 12()vmmgMR+= ① 当剪断两物体之间的轻线后，轻线对小球的拉力减小，不足以维持小球在半径为 R 的轨道上继续做匀速圆周运动，于 是小球沿切线方向逐渐偏离原来的轨道，同时轻线下端的物体 m1 逐渐上升，且小球的线速度逐渐减小．假设物体 m1 上升 高度为 h，小球的线速度减为 v 时，小球在半径为（R＋h）的轨道上再次做匀速圆周运动，根据牛顿第二定律有 2 1 vmg MRh= + ② 再选小球 M、物体 m1 与地球组所的系统为研究对象，研究两物体间的轻线剪断后物体 m1 上升的过程，由于只有重力 做功，所以系统的机械能守恒．选小球做匀速圆周运动的水平面为零势面，设小球沿半径为 R 的轨道做匀速圆周运动时 m1 到水平板的距离为 H，根据机械能守恒定律有 22 01 1 11()22MvmgHMvmgHh− =− − ③ 以上三式联立解得 12(3 ) 3 mmgRv M += 解法二：（转化观点）与解法一相同，首先列出①②两式，然后再选小球、物体 m1 与地球组成的系统为研究对象，研 究两物体间的轻线剪断后物体 m1 上升的过程，由于系统的机械能守恒，所以小球动能的减少量等于物体 m1 重力势能的增 加量．即 22 01 11 22MvMvmgh−= ④ ①、②、④式联立解得 12(3 ) 3 mmgRv M += 点评：比较上述两种解法可以看出，根据机械能守恒定律应用守恒观点列方程时，需要选零势面和找出物体与零势面 的高度差，比较麻烦；如果应用转化观点列方程，则无需选零势面，往往显得简捷． 【例 5】 解析：（1）第一颗子弹射入木块过程中动量守恒 01 1mv MV mu MV ′− =+ ① 解得： 1v′ =3m/s ② 木块向右作减速运动加速度 5MgagM μ μ===m/s2 ③ 木块速度减小为零所用时间 1 1 vt a ′= ④ 解得 t1 =0.6s<1s ⑤ 所以木块在被第二颗子弹击中前向右运动离 A 点最远时，速度为零，移动距离为 2 1 1 2 vs a ′= 解得 s1=0.9m． ⑥ （2）在第二颗子弹射中木块前，木块再向左作加速运动，时间 t2=1s－0.6s=0.4s ⑦ 速度增大为 v2=at2=2m/s（恰与传送带同速） ⑧ 向左移动的位移为 2 22 1 0.4m2sat== ⑨ 所以两颗子弹射中木块的时间间隔内，木块总位移 S0=S1－S2=0.5m 方向向右 ⑩ 第 16 颗子弹击中前，木块向右移动的位移为 15 0.5 7.5ms = ×= ○11 第 16 颗子弹击中后，木块将会再向右先移动 0.9m，总位移为 0.9m＋7.5=8.4m>8.3m 木块将从 B 端落下． 所以木块在传送带上最多能被 16 颗子弹击中． （3）第一颗子弹击穿木块过程中产生的热量为 2222 10 1 1 11 11 22 22QmvMVmuMV′=+ −− ○12 木块向右减速运动过程中板对传送带的位移为 11 1Svts′ = + ○13 产生的热量为 Q2= MgSμ ′ ○14 木块向左加速运动过程中相对传送带的位移为 12 2SVts′′ = − ○15 产生的热量为 3QMgsμ ′′= ○16 第 16 颗子弹射入后木块滑行时间为 t3 有 2 13 3 1 0.82vt at′ −= ○17 解得 t3=0.4s ○18 木块与传送带的相对位移为 S=v1t3＋0.8 ○19 产生的热量为 Q4= Mgsμ ○20 全过程中产生的热量为 Q=15(Q1＋Q2＋Q3)＋Q1＋Q4 解得 Q=14155.5J ○21 【例 6】 解析：运动分析：当小车被挡住时，物体落在小车上沿曲面向下滑动，对小车有斜向下方的压力，由于 P 的作用小车处于静止状态，物体离开小车时速度为 v1，最终平抛落地，当去掉挡板，由于物对车的作用，小车将向左加速 运动，动能增大，物体相对车滑动的同时，随车一起向左移动，整个过程机械能守恒，物体滑离小车时的动能将比在前一种 情况下小，最终平抛落地，小车同时向前运动，所求距离是物体平抛过程中的水平位移与小车位移的和．求出此种情况下， 物体离开车时的速度 v2，及此时车的速度 2v′ 以及相应运动的时间是关键，由于在物体与小车相互作用过程中水平方向动量 守恒这是解决 v2、 2v′ 间关系的具体方法． （1）挡住小车时，求物体滑落时的速度 v1，物体从最高点下落至滑离小车时机械能守恒，设车尾部（右端）离地面高 为 h，则有 2 1 1()2mg H h mv−= ， ① 由平抛运动的规律 s0=v1t ② 21 2hgt= ． ③ （2）设去掉挡板时物体离开小车时速度为 v2，小车速度为 2v′ ，物体从最高点至离开小车之时系统机械能守恒 22 22 11()22mg H h mv Mv′−= + ④ 物体与小车相互作用过程中水平方向动量守恒 220Mv mv′ − = ． ⑤ 此式不仅给出了 v2 与 2v′ 大小的关系，同时也说明了 v2 是向右的． 物体离开车后对地平抛 22s vt′= ⑥ 21 2hgt′= ⑦ 车在 t′ 时间内向前的位移 22s vt′ ′′= ⑧ 比较式⑦、③，得 ,tt′ = 解式①、④、⑤，得 2122,MmvvvvMm M ′==+ ． 此种情况下落地点距车右端的距离 22 22 2 1 0()(1)mMmM Mmss s v vt vt vtsMMMmM + +′′=+= + =+ = =+ ． 点评：此题解题过程运用了机械能守恒、动量守恒及平抛运动的知识，另外根据动量守恒判断 m 离车时速度的方向及 速度间的关系也是特别重要的． 【例 7】 解析：（1）设第一次碰墙壁后，平板车向左移动 s，速度为 0．由于体系总动量向右，平板车速度为零时， 滑块还在向右滑行． 由动能定理 2 0 10 2MgS mvμ−=− ① 2 0 2 mvs Mgμ= ② 代入数据得 222 1 0.33m20.43103s ×===××× ③ （3）假如平板车在第二次碰撞前还未和滑块相对静止，那么其速度的大小肯定还是 2m/s，滑块的速度则大于 2m/s， 方向均向右．这样就违反动量守恒．所以平板车在第二次碰撞前肯定已和滑块具有共同速度 v．此即平板车碰墙前瞬间的速 度． 00()MvmvMmv−=+ ④ ∴ 0 M mvvM m −= + ⑤ 代入数据得 0 1 0.4m/s5vv== ⑥ （3）平板车与墙壁第一次碰撞后到滑块与平板又达到共同速度 v 前的过程，可用图（a）（b）（c）表示．（a）为平板 车与墙壁撞后瞬间滑块与平板车的位置，图（b）为平板车到达最左端时两者的位置，图（c）为平板车与滑块再次达到共 同速度为两者的位置．在此过程中滑块动能减 少等于摩擦力对滑块所做功 Mgsμ ′ ， 平板车动能减少等于摩擦力对平板车所做功 Mgsμ ′′ （平板车从 B 到 A 再回到 B 的过程中摩擦力做功为零），其中 s′ 、 s′′ 分别 为滑块和平板车的位移．滑块和平板 车动能总减少为 1,Mglμ 其中 1lss′′′=+ 为滑 块相对平板车的位移．此后，平板车 与墙壁发生多次碰撞，每次情况与此类似，最 后停在墙边．设滑块相对平板车总位 移为 l，则有 2 0 1 ()2 M mv Mglμ+= ⑦ 2 0() 2 M mvl Mgμ += ⑧ 代入数据得 252 5 0.833m20.43106l ×===××× ⑨ l 即为平板车的最短长度． 【例 8】 解析：本题应用动量守恒，机械能守恒及能量守恒定律联合求解。 在 m 下落在砂箱砂里的过程中，由于车与小泥球 m 在水平方向不受任何外力作用，故车及砂、泥球整个系统的水平方 向动量守恒，则有： 01()MvMmv=+ ① S′′ S′ A B C D （a） （b） （c） 此时物块 A 由于不受外力作用，继续向右做匀速直线运动再与轻弹簧相碰，以物块 A、弹簧、车系统为研究对象，水 平方向仍未受任何外力作用，系统动量守恒，当弹簧被压缩到最短，达最大弹性势能 Ep 时，整个系统的速度为 v2，则由动 量守恒和机械能守恒有： 01 2()(2)MvMmvMmv++ = + ② 22 2 01 1 11 1() (2)22 2pMv M mv E M mv++=++ ③ 由①②③式联立解得： 2 2 02( )(2 )P MmEvMm Mm= ++ ④ 之后物块 A 相对地面仍向右做变减速运动，而相对车则向车的左面运动，直到脱离弹簧，获得对车向左的动能，设刚 滑至车尾，则相对车静止，由能量守恒，弹性势能转化为系统克服摩擦力做功转化的内能有： pMgL Eμ = ⑤ 由④⑤两式得： 22 0 2( )(2 ) mvL g Mm Mmμ= ++ 跟踪练习 1．【答案】 D 【解析】 在△t1 时间内，I1=F△t1=mv=△p1，在△t2 时间内．I2=F△t2=2mv－mv=mv=△p2 ∴I1=I2 又 2222 12 1113,(2)2222W mv W m v mv mv==−= ∴W1vB，弹簧还将继续缩短，所以这种状态是能够出现的． 若 0 2 ,3 vv =− 则表示 B 球与板碰撞后 A、B 向左运动． B 球与板碰撞后 B 和 A 动量守恒 0 22333AB vmv mv mv m−= =− ⑧ 由⑥⑧可得 0 0 3,42AB vvvv== 此时 A、B 球的总动能 22 2 2 20 00 11 13192()()22 42216kAB vEmvmvmmvmv=+=+ =总 kE 总 大于 A 球最初的动能 2 0mv ，因此 0 3 2Bvv= 这种状态是不可能出现的 因此，必须使 B 球在速度为 0 2 v 时与挡板发生碰撞． 12．【解析】 （1）设 C 球与 B 球粘结成 D 时，D 的速度为 v1，由动量守恒，有 01()mv m m v= + ① 当弹簧压至最每短时，D 与 A 的速度相等，设此速度为 v2，由动量守恒，有 1223mv mv= ② 由①②两式得 A 的速度 20 1 3vv= （2）设弹簧长度被锁定后，贮存在弹簧中的势能为 Ep，由能量守恒，有 22 12 112322 pmv mv E=+ 撞击 P 后，A 与 D 的动能都为零．解除锁定后，当弹簧刚恢复到自然长度时，势能全部转变成 D 的动能，设 D 的速度 为 v3，则有 2 3 1 (2 )2pEmv= 以后弹簧伸长，A 球离开挡板 P，并获得速度．当 A、D 的速度相等时，弹簧伸至最长，设此时的速度为 v4，由动时守 恒，有 3423mv mv= 当弹簧伸到最长时，其势能最大，设此势能为 pE′ ，由能量守恒，有 22 34 112322 pmv mv E′=+ 解以上各式得 2 0 1 36pEmv′ = 说明：该题以“双电荷交换反应”为背景，考查的是动量守恒和机械能守恒定律的知识，又考查了理解能力，推理能 力，分析综合能力，突出了对物理过程的考查．考生必须首先弄清整个物理因素，针对不同的物体在各个阶段的受力情况， 再确定其运动所遵循的规律．分析物理过程是解决这个问题的关键，现具体过程分析如下： ①C 以 v0 与 B 发生完全非弹性碰撞，弹簧长度不能突变，A 可看成静止． ②BC 形成一体 D 向左压缩弹簧，A 的速度增大，D 的速度减小，两者共速，弹簧压缩最短． ③弹簧锁定后与挡板相碰而静止． ④解除锁定，D 向右加速，墙对 A 的作用力不断减小，达到原长时作用力为零． ⑤弹簧达到自然长度后，D 继续向右运动逐渐减速，而 A 开始向右加速，弹簧伸长到最长时，两物体的速度相等，这 时弹簧的弹性势能最大． 根据上面的分析，把复杂的物理过程分解为几个简单的过程，同时发掘出弹簧压缩最短和伸长最长的隐含条件，运用 物理规律列方程，就可达到准确解题的目的． 13．【解析】 （1）当 A、B、C 三者的速度相等时弹簧的弹性势能最大 由于 A、B、C 三者组成的系统动量守恒， ()( )A BABCAmmvmmmv′+ =++ 解得 (2 2) 6 3m/s224Av +×′ ==++ （2）B、C 碰撞时 B、C 组成的系统动量守恒，设碰后瞬间 B、C 两者速度为 v′， 则 ()BBCmv m m v′=+ 26 2m/s24v ×′ ==+ 设物 A 速度为 Av′ 时弹簧的弹性势能最大为 pE ，根据能量守恒 22 2 22 111() ( )222 111(24)2 26 (224)312J222 p BC A ABCAE m mv mv m m mv′′=+ + −++ =×+× +××−×++×= （3）A 不可能向左运动 系统动量守恒， ()A BAABCBmv mv mv m m v+ =++ 设 A 向左，vA<0，则 vB>4m/s 则作用后 A、B、C 动能之和 22 211 1()()48J22 2AA B C B B C BEmvmmvmmv′ = ++>+= 实际上系统的机械能 21 ( ) 12 36 48J2p ABCAEE mmmv′=+ ++ =+= 根据能量守恒定律，E′>E 是不可能的． 14．【解析】令 A、B 质量均为 m，A 刚接触 B 时的速度为 v1（碰前）． A 克服阻力做功： 2 2 0 1 122 mv mv mglμ−= ① A、B 碰撞过程中动量守恒，令碰后 A、B 的共同速度为 v2，有 mv1=2mv2 ② 碰后 A、B 先一起向左运动，接着 A、B 一起被弹回，在弹簧恢复到原长时，设 A、B 的共同速度为 v3，在这一过程中， 弹簧的弹性势能始末状态都是零，只有克服摩擦力做功 23 22 2 (2 ) (2 ) (2 ) (2 )22 mv mv mg lμ−= ③ 此后 A、B 开始分离，A 单独向右滑动到 P 点停下，克服阻力做功 2 3 12 mv mglμ= ④ 由以上各式得 012(10 16 )vgllμ=+ ⑤ 15．【解析】 C 有可能停在 B 上，也有可能停在 A 上，还有可能滑离 A，先假设停在 B 上，由动量守恒定律得： 01(2)mv m M v=+ ． 设 C 在 B 上滑动距离为 x，木板 B 的位移为 s，则 C 对地的位移为 s＋x， 由功能关系得：对木板： 2 1 1 22mg Mvμ =× 对 C： 22 01 11() ,22mg s x mv mvμ += − 所以得： 22 01 11(2),22mgx mv m M vμ =−+ 从而解得 2 0 1.6m(2 ) Mvx gMmμ==+ ，大于板长，C 将滑离 B 板． 设 C 刚滑到 A 板上速度为 0v′ ，此时 AB 两板的速度为 vB，由动量守恒得 002,Bmv mv Mv′= + 由功能关系得： 22 2 00 11 1222 2Bmgl mv mv Mvμ ′=− −× ∴ 0 824224 20 5Bvv±±′== 合理的解是： 8240.155m/s20Bv −== 0 2241.38m/s5v +′ == 当 C 滑到 A 上，B 以 0.155m/s 的速度匀速运动了，设 C 停在 A 上，速度 vA，相对 A 滑行距离为 y，由动量守恒得： 0 ()BAMvmvmMv′+=+ 解得： Av = 0.563m/s，由动能关系得： 22 2 0 111()222BAmgy mv Mv m M vμ ′=+−+ 代入数据得 y=0.50m，小于 A 板长度，C 不能滑离 A 板，最后 A、B、C 的速度分别为 vA=0.563m/s vB=0.155m/s， 0.563CAvv== m/s 16．【解析】 对物体，滑动摩擦力 f 做负功， 由动能定理得 22 0 11() ,22tf ds mv mv−+= − 即 f 对物体做负功，使物块动能减少． 对木块，滑动摩擦力 f 对木块做正功，由动能定理得 21 2fsMV= ， 即 f 对木块做正功，使木块动能增加，系统减少的机械能为 22 2 0 111 () ,222tmv mv MV f d s fs fd−− =+−= ① 本题中 f mgμ= ，物块与木块相对静止时 tvV= ， 则上式可简化为 22 0 11(),22 tmgd mv m M vμ =−+ ② 又以物块、木块为系统，系统在水平方向不受外力，动量守恒， 则 0 (),tmv m M v=+ ③ 联立②、③式得 2 0 2( ) Mvd g Mmμ= + ． 故系统机械能转化成内能的量为 22 00 2( )2() MvMmvQfdmg g Mm Mmμ μ== =++ ． 评析：系统内一对滑动摩擦力做功之和（净功）为负值，在数值上等于滑动摩擦力与相对位移的乘积，其绝对值等于 系统机械能的减少量，即系统机械能转化为系统的内能，记为 Qfs= 相对 ． 上述情况①和②同样符合该规律，掌握了它可使许多计算简化． 专题三 电场和磁场 典型例题 [例 1] 解析：A 点拨：电场线从+Q 发出，到接地的很大的薄金属板，并与金属板垂直。根据电场线可判断①正确，M 点的电场是+Q 的电场与金属板的感应电荷的电场的叠加，故②错误；N 点与金属板接地，所以电势为零，但电场强度不为 零，故③正确，④错误。 【例 2】 解析：对 A 进行受力分析，设悬线的拉力为 T，水平线的拉力为T ′ ，在竖直方向上受重力和悬线的拉力而平 衡： mgT =030cos ① 在水平方向上，小球受电场力、电荷间的为库仑力、悬线的水平拉力和水平线的拉力而平衡： Tl qkTEq ′++= 2 2 030sin ② 要两球处于题设条件的平衡状态，则对水平线的受力要求为： 0≥′T ③ 联解①②③得到： 23 3 l kq q mgE +≥ 【例 3】 解析：电子经 U1 加速后，设以 0v 的速度垂直进入偏转电场，由动能定理得： 1 2 0 02 1 eUmv =− ① 电子在偏转电场中运动的时间 t 为： 0v lt = ② 电子在偏转电场中的加速度 a 为： dm eUa 2= ③ 电子在偏转电场中的偏转量 h 为： 2 2 1 ath = ④ 由以上四式联解得到示波管的灵敏度 2U h 为： 1 2 2 4dU l U h = 可见增大 l 、减小 U1 或 d 均可提高示波管的灵敏度。 【例 4】解析：由于电容器与电源相连，则电容器两极板的电压不变，根据平行板电容器电容 kd SC π ε 4= 可知，当 d 增大 S 不变时，电容 C 减小；又因 U QC = 可得，电荷量减小；又由 d UE = 可知，场强 E 减小，故 A 选项正确；当 S 增 大， d 不变时，C 增大，Q 增大，E 不变，所以 B 选项错误；当 d 减小，S 增大时，C 增大，Q 增大，E 增大，所以 C 选项 正确；当 S 减小， d 减小时，电容 C 不一定增大，Q 也不一定增大，但 E 一定增大，所以 D 选项错误。可见本题 AC 选项 正确。 【例 5】 解析：如图所示，电场对粒子加速，由动能定理得： Uqmv =2 02 1 m Uqv 2 0 = ① 由于粒子在电场加速过程中做匀加速直线运 动，则加速的时间 1t 为： 00 1 2 2/ v d v dt == ② 粒子在偏转电场中做类似平抛运动，其加速度 a 为： Lm Uqa = 粒子通过偏转电场的时间 2t 为： Uq mLv Lt 20 2 == ③ 粒子在偏转电场中的侧移距离 y 为： 42 1 2 2 Laty == ④ 侧向速度 yv 为： m Uqatvy 22 == 则粒子射出偏转电场时的速度 v 为： m Uqvvv y 2 522 0 =+= ⑤ θ O L L U S d U B D R 以速度 v 进入磁场做匀速度圆周运动的洛仑兹力为向心力，设运动半径为 R： R vmBqv 2 = q Um BBq mvR 2 51== ⑥ 则磁场宽度 D 为： 162 5 2 51 2 2 22 L qB Um q Um ByRRD −+=−+= ⑦ 粒子在磁场中做匀速圆周运动的周期T ′ 为： Bq m v RT ππ 22 ==′ 24/ 2/ == L Ltgθ 所以 2arctg=θ 所以粒子在磁场中运动的时间 3t 为： Bq arctgmTt )2(2 2 )22( 3 −=−′= π π θπ ⑧ 粒子从 S 出发到回到 S 的周期 T 为： Bq arctgm Uq mLUq mdtttT )2(2 222422 321 −++=++= π 偏转电压正负极换向时间 t 为： Bq arctgm Uq mLUq mmTt )2( 2222 −++== π 【例 6】 解析：正离子每次经过缝隙时都能得到加速必须满足在筒中飞行时间 2 Tt = 所以第一个筒长度 211 TvL ⋅= 进入第二个筒时速度为 v2，则 2 1 2 2 2 1 2 1 mvmvqU −= ① 第二个筒长 222 TvL ⋅= 进入第三个筒的速度为 v3，则 2 22 12 32 1 mvmvqU −= ② 第三个筒长 233 TvL ⋅= 进入第 n 个筒的速度 vn 满足 2 1 2 2 1 2 1 −−= nn mvmvqU ③ 第 n 个筒的长度为 2 TvL nn ⋅= ， 解以上各式得： m qUnvfm qUnvTLn )1(2 2 1)1(2 2 2 1 2 1 −+=−+= L3,2,1=n 由动能定理得： nqUmvEk =− 2 12 1 nqUmvEk += 2 12 1 L3,2,1=n 【例 7】 解析：设带电粒子带电为 q+ ，根据题目条件可知，要使粒子平衡，则下极板带正电，上极板带负电，且有： mgqE =1 ① 当电场由 E1 变到 E2，但方向不变，时，有 mgqE >2 ，粒子在 E2 的方向上做匀加速度直线运动，粒子从 A 运动到 B， 设加速所用时间为 1t ，此时 E2 反向，设粒子的速度为 1v ，此后粒子向上做加速度为 2a 减速度运动，直到速度为零，到 达 B 点；此后粒子在电场力和重力作用下向下做初速度为零的匀加速直线运动，加速度大小为 2a ，回到出发点 A。设粒 子从 B 到 A 的时间为 2t 。 2 112 1 taS AB = ② 粒子从 B 点经 C 点回到 A 点，有： 2 221 2 1 tatvS −=− ③ 由于 111 tav = ④ 所以有： 2 22211 2 1 tattaS BA +−= ⑤ 由题意可知： 21 tt = ⑥ 联解得： 213 aa = 即： 1212 )(3 qEqEqEqE +=− 得到： 21 2 1 EE = 【例 8】 分析：（1）微粒运动到 O 点之前要受到重力、电场力和洛仑兹力作用，如图所示．在这段时间内微粒做匀速 直线运动，说明三力合力为零．由此可得出微粒运动到 O 点时速度的大小和方向．（2）微粒运动到 O 点之后，撤去磁场， 微粒只受到重力、电场力作用，其合力为一恒力，与初速度有一夹角，因此微粒将做匀变速曲线运动，如图所示．可利用运 动合成和分解的方法去求解． 解析：因为 Nmg 4104 −×= 电场力为： NEqF 4103 −×== 则有： 222 )()()( mgEqBqv += 所以得到： v=10m/s 所以 θ=37° 因为重力和电场力的合力是恒力，且方向与微粒在 O 点的速度方向垂直，所以微粒在后一段时间内的运动为类平抛运 动．可沿初速度方向和合力方向进行分解。设沿初速度方向的位移为 1S ，沿合力方向的位移为 2S ，则 x y B E • P O f Eq v S2 G′ S1 因为 vtS =1 2 22 2 )()( 2 1 tm mgEqS += 037cos vtOP = 所以 P点到原点 O 的距离为 15m； O点到 P 点运动时间为 1. 2s． 跟踪练习 1.解析：P、Q 在 O 点的合场强为零，沿着 Oab 线到无穷远处，P、Q 的合场强也为零，可见沿 Oab 线远离 O 点时，合场强 是先增大后减小，故 aE 不一定大于 bE ，而电势离电荷越远越低，必有 aU 大于 bU ，所以 B 选项正确。 2.解析：由于电荷两次都是从电场外移入电场的，故选电场外电势为零解题方便。 由 qUW = 可得 q WU = Vq WUU OA AOA 2 5 3 10610 1060 ×−=×−==−= − − VU A 2106×=∴ Vq WUU OB BOB 21020 ×==−= VU B 3102×−=∴ A、 B 两点间电势差：UAB=UA－UB=6×102－(－2×103)=2.6×103V 当电荷 q′ 由 A 移到 B 时电场力做功： JUqW ABAB 235 102.5106.2102 −− ×−=×××−=′=′ 3.解析：用相似三角形法，得到 l mg l T = ，故得到 mgT = 与偏角无关。所以 C、D 选项正确。 （1） （2） （3） （4） 图 13—4—答 4.解析：.图 13—4—答（1）中虚线表示 A、B 球原来的平衡位 置，实线表示烧断后重新达到平衡的位置，其中α 、β 分别表示细线 OA、AB 与竖直方向的夹角。A 球受力如图 13—4—答（2）所示：重力 mg，竖直向下；电场力 qE，水平向左； 细线 OA 对 A 的拉力 T1，方向如图；细线 AB 对 A 的拉力 T2，方向如图。由平衡条件： qETT =+ βα sinsin 21 ， βα coscos 21 TmgT += mg T2 Eq B β A B O Eq T1 T2 α β mg A α A B β B 球受力如图 13—4—答(3)所示：重力 mg，竖直向下；电场力 qE，水平向右；细线 AB 对 B 的拉力 T2，方向如图。由 平衡条件： qET =βsin2 ， mgT =βcos2 ,联立以上各式并代入数据得 0=α ， 045=β ，由此可知，A、B 球重 新达到平衡的位置如图 13—4—答（4）所示。与原来位置相比，A 球的重力势能减少了，EA=mgl(1－sin60°)，B 球的重力 势能减少了 )45cos60sin1( 00 +−= mglEB ，A 球的电势能增加了 060cosqElWA = ，B 球的电势能减少了 )30sin45(sin 00 −= qElWB ，两种势能总和减少了 BAAB EEWWW ++−= ，代入数据解得： W=6.8×10－2J 5.解析：设电子经电场加速后的速度为 0v 1 2 02 1 eUmv = 得到： m eUv 1 0 2= ① 设电子射出平行板的偏角为ϑ ，两极板间的距离为 d ，电子的加速度为 a dm eUa 2= ② 而电子在平行板中运动的时间为： 0v lt = ③ 电子的偏转角θ 为： 0v at v vtg x y ==θ ④ 由①②③④联解得： 1 2 2dU lUtg =θ 所以 C 选项正确。 6. 解析：（1）计算电子打到记录纸上的最高点的坐标，设 v0 为电子 A、B 板的中心线射入电场时的初速度，则 0 2 02 1 eUmv = ，电子在中心线方向的运动为匀速运动，设电子穿过 A、B 板的时间为 t0，则 00tvl = ，电子在垂直 A、B 板方向的运动为匀加速直线运动，对于恰能穿过 A、B 板的电子，在它通过时加在两板间的电压 UC 应满足 2 02 1 2 1 tmd eUd c= ， 联立上面三式得 VUl dU C 202 02 2 == ，此电子从 A、B 板射出时沿 y 方向的分速度为 0tmd eUv c y = ，以后，此电子做 匀速直线运动，它打在记录纸上的点最高。设纵坐标为 y。由答图可得， 0 2 v v b dy y= − 7. 解析：静电计是用来测量带电体和大地间的电势差的，平行板电容器与电源断开，则电容器所带的电量几乎不变， 将 B 板向上移动时，两极板间的正对面积减小，电容减小，由 C QU = 可知，U 增大，所以选项 D 正确。 8.解析：由于平行板电容器已充电，所以电量不变，当上极板下移后，极间距离变小，根据 kd SC π ε 4= 可知，电容 C 增大，根据 U QC = 可知，极板间电压变小；由电场强度 d UE = 和 C QU = 可知， S kQE ε π4= ，与极间距离 d 无关， 所以电场强度 E 不变；由 EdU = 可知，由于 P 点到接地板间的距离不变，所以 P 点的电势不变。由电势能与电势电量的 关系 q WU = 可知, UqW = 不变。所以选项 BD 正确. 9.解析：粒子进入磁场做圆周运动，由 于不知道粒子的带电性质和 磁场的方向，因此其轨迹并不确定，但只有 两种情形，要么如图（甲）所 示，要么如图（乙）所示， 首先分析图甲：作 v0 的垂直线段，切取 OC＝0，C 即为圆面积心，画出其轨迹如图， qB mvR 0= 。由几何关系可得 θ2=∠OCP ，所以粒子在磁场中飞行的时间为 qB m qB mt )(22 2 22 θππ π θπ −=⋅−= P 点的坐标为 θθ sin2sin2 0 === qB mvRx 再看图乙：由几何关系得 θ2=∠OCP ，粒子在磁场中飞行的时间为 qB mt θ2= ，P 点的坐标为 θsin2 0 qB mvx −= 。 10. 解析（1）粒子带正电；（2）粒子由 N 至 O 在电场力作用下作初速为零的匀加速直线运动，到 O 后进入磁场后做 匀速圆周运动，作半圆运动后，回到 x 轴进入电场，在电场力作用下先做匀减速直线运动直至速度为零再向上作初速为零的 匀加速直线运动…重复进行，如图所示轨迹，最后到 达 M 点，粒子在电场中，运动距 离 b 到达磁场区域，电场力做正功，据动能定理有： 02 1 2 −= mvqEb 。从磁场再 次进入电场，设运动的路程为 S，粒子则克服电场力 做 功 。 据 动 能 定 理 有 ： 2 2 10 mvqES −=− ，上两式知 bS = ，粒子在磁 场中偏转后刚好过M点的条件是 L 应为圆轨道半径 R 的 2N 倍（ 其 中 N＝1、2、3……）， qE mvNNRL 22 == ， Nm qBLv 2=∴ ，而 qE mvbNO 2 2 == ，∴ 满足条件的 N 至 O 距离 2 22 8EmN LqBb = （其中 N＝1、2、3……） （3）要使粒子从 N 到 M 的时间最短则应 N＝1。即粒子从 N 到 O，再由做一个半圆运动恰好要到 M 点， OMNo ttt += ， 而 N＝1， m qBLv 2= ，由动量定理： mvqEtNO = ， E BL mqE qBLmqE mvtNO 22 =⋅==∴ ， 而 qB m qB mTTOM ππ =⋅== 2 2 1 2 ，所以 N→O→M 最短费时 qB m E BLt π+= 2 11.AB，点拨：画出 B 极板的电势变化的图线，分析电子的运动状态，可结合速度图线进行分析。 y xM N 0,- L,0 O O C P θ v0 P θ O C （甲） （乙） 12..解析：设碳离子到达 b 处时的速度为 v1，从 c 端射出时的速度为 v2，由能量关系得： eUmv =2 12 1 ① neUmvmv += 2 1 2 2 2 1 2 1 ② 进入磁场后，碳离子做圆周运动，可得： R vmBnev 2 2 2 = ③ 由以上三式可得： e nmU BnR )1(21 += ④ 由④及题给数值可解得： mR 75.0= 13. 解析: （1）粒子每经狭缝 AB 一次，加速一次，增加动能 qU，故绕行 n 圈（经 n 次加速）回到 A 板时获得的总 动能为 nqUEn = （ 2 ）由 2 2 1 nmvmqU = 和 R vmBqv n nn 2 = 得粒子绕行 n 圈时，磁场的磁感应强度递增到 q nmU Rm nqU qR mBn 212 == （3）A、B 间距离远小于半径 R，粒子穿过其间所花时间 忽略不计，故粒子绕行 n 圈所用时间 nqU mRv Rt n n 1 222 ⋅== ππ 粒子绕 n 圈所需要的时间 123 11 12(1 )2 23 ntt t t t mR qU n π = + + +⋅⋅⋅⋅⋅⋅+ = + + +⋅⋅⋅⋅⋅⋅+ （4）按题意要求画出 u—t 的函数图象如图 15—5—答 3 所示（是时间间隔越来越小，加速时间越来越短的等幅脉冲电 压） (5)不可以。因为这样粒子在 A、B 之间飞行时电场对其做功＋qU，使之加速，在 A、B 之外飞行时电场又对其做功－qU， 使之减速，粒子绕行一周电场对其所做总功为零，能量不会增大。 14. 解析：设质点 P 的质量为 m，电量为 q，当 A、B 间为 U0 时质点为静止平衡状态，有： mgqd U =0 ① 当极板间的电压为 2U0 时，质点 P 的加速度向上，由 maF = 得： mamgqd U =−02 ga = ② 当电压为零时，质点 P 的加速度又为 g ，方向向下。 要满题意要求，则在 0=t 开始，P 先受合力向上，加速度为 ga = ，做初速度为零的匀加速度运动，设经时间 1τ ，质 u U 0 t1 t2 t3 t 图 15—5—答 3 点 P 的速度为 1v ，此时电压变为零，P 在重力作用下做匀减速运动，再经 1τ ′ ，P 点正好到达 A 板且速度为零，故有： 11 τgv = ， 011 =′− τgv ③④⑤⑥ 则 2 111 2 1 2 1 2 1 2 1 τττ ′−′+= gvgd 得到： g d 2 2 11 =′= ττ 因为 g dt 2 2 11 == τ 了在重力作用下，P 由 A 极板处向下做匀加速度经过 3τ 的时间到达中点，速度变为 2v ，方向向下，这时加下电压使 P 做 ga = 匀减速运动，经过 2τ ′ 到达 B 板且速度为零，故有： 22 τgv = ， 220 τ ′−= gv 2 222 2 2 2 1 2 1 τττ ′−+= gvgd 由以上各式可知： g d=′= 22 ττ g dtt )12(2112 +=+′+= ττ 此后 P 在电场力和重力的共同作用下，由 B 处向上做加速度为 g 匀加速运动，到达中点时，速度为 3v ，此时电场为 零，此后 P 在重力作用下继续向上运动到达 A 极板时的速度为零。所以有： 33 τgv = 330 τ ′−= gv 2 333 2 3 2 1 2 1 τττ ′−+= gvgd 得到： g d=′= 33 ττ g dtt )32(3223 +=+′+= ττ 同理可知： g dt )52(4 += g dntn )322( −+= （ )2≥n 15.解析：因 OBOCODBCBD === 2 ，则 B、C、D 三点在以 O 为圆心的同一圆周上，是 O 点处点电荷 Q 产生 的电场中的等势点，所以，q 由 D 到 C 的过程中电场中电场力作功为零。由动能定理得， 22 2 1 2 1 mvmvmgh e −= ① 而 2 360sin 0 lBDh == glvv 32 0 −= 质点在 C 受三个力的作用；电场 F，方向由 C 指向 O 点；重力 mg，方向竖直向下；支持力 N，方向垂直于斜面向上。 由牛顿第二定律， cmaFmg =− 00 30cos30sin ② 而 2l QqKF = ③ 解得： 22 3 2 1 ml KQqgac −= 专题四 电磁感应与电路 典型例题 【例 1】 解析：在从图中位置开始（t =0）匀速转动 60°的过程中，只有 OQ 边切割磁感线，产生的感应电动势 2 1 1 2EBlω= ，由右手定则可判定电流方向为逆时针方向（设为正方向）．根据欧姆定律得， 2 1 1 (0 )23 E BlItRR ω π ω== <≤ ． 导线框再转过 30°的过程中，由于 ΔΦ =0， 则 2 23 50( ), ( )32 226 BlItI tR π πωππ ω ωωω=< = <≤≤顺时针方向． 2 45 540( ) ( )623 BlItI tR π πωππ ω ωωω=< = <≤≤逆时针方向 2 67 43 3110( ) ( )32 226 BlIt I tR π πωππ ω ωωω=< = <≤≤顺时针方向 8 11 20( )6Itπ π ω ω=<≤ 综合以上分析可知，感应电流的最大值 2 0 2 BlI R ω= ， 频率 f π ω= ．其 I—t 图象如图 4—2 所示． 答案：（1） 2 0 ;2 BlIfR ω π ω== （2）如图 4—2 所示． 【例 2】 解析：P 向 b 移动，电路中总电 阻变大，由闭合电路的欧姆定律、 欧姆定律以及电路的性质从而可以判断 U1、U2 的变化情况． 当 P 向 b 移动时，电路中总电阻变大，由闭 合电路的欧姆定律可知电路中总 电路 I 变小，由欧姆定律得 U2=IR 变小，再由闭 合电路欧姆定律得 U1=E－Ir 变 大，故本题正确答案应选 A． 【例 3】 解析： （1）由题意可知，金属杆在磁场中的运动分为两个阶段：先沿 x 轴正方向做匀减速运动，直到速度 为零；然后 x 轴负方向做匀加速直线运动，直到离开磁场，其速度一时间图象如图 4—5 所示．金属杆在磁场中运动切割磁 感线，闭合回路产生感应电流，所以回路中感应电流持续的时间 0 1 22 vtt a== ． （2）当金属杆沿 x 轴正方向运动的速度为 0 2 v 时，对应的 x 坐标 x1`满足： 20 01() 2 ,2 v vax=− 解得 x1= 2 03 8 v a ． 则在 x1 处的磁感强度 2 0 11 3 8 kvBkx a== 此时回路中的感应电动势， 3 00 1 3 216 vkdvEBd a== 图 4—2 图 4—5 金属杆所受的安培力大小 25 2 01 1 2 9 128 kvdEFBIdBdR aR == =安 方向沿 x 轴负方向 由牛顿第二定律得 F＋F 安=ma 所以，此时作用于金属杆的外力 25 2 0 2 9 128 kvdFma aR =− 方向沿 x 轴负方向． 答案：（1） 02v a （2） 3252 00 2 39;16 128 kdv k v dmaa aR − 【例 4】 解析： （1）设线圈匀速穿出磁场的速度为 v′， 此时线圈中产生的感应电动势为 EBLv′= ． ① 产生的感应电流为 EI R= ② 线圈受到的安培力为 F=BIL ③ 此过程线圈受到的重力与安培力平衡 mg=F ④ 联立①②③④式，得 22 mgRv BL ′ = ⑤ 设线圈的上边刚好进入磁场时速度为 v，线圈全部在磁场里运动的过程中，根据能量守恒定律 2211()22mg h b mv mv′−= − ⑥ 联立⑤⑥解得 2 22()2()mgRvghb BL =−− ⑦ （2）设线圈从开始下落到刚好完全进入磁场所用时间为 t，根据动量定理 0Fmgt I mv− =− ⑧ 根据法拉第电磁感应定律 BLbE tt ΔΦ== ⑨ 线圈中产生的平均电流 EI R= ⑩ 故安培力的冲量 FIFtBLIt== ○11 联立⑨⑩○11 得， 22 F BLbI R= ○12 将⑦和○12 代入⑧解得 22 2 2 44 2( )BLb mR h bt mgR gBL −=+ − 【例 5】 解析：ab 棒向 cd 棒运动时，两棒和导轨构成的回路面积变小，磁通量发生变化，于是产生感应电流．ab 棒受到与运动方向相反的安培力作用做减速运动，cd 棒则在安培力作用下做加速运动，在 ab 棒的速度大于 cd 棒的速度时， 回路中总有感应电流，ab 棒继续减速，cd 棒继续加速．两棒速度达到相同后，回路面积保持不变，磁通量不变化，不产生 感应电流，再棒以相同的速度 v 做匀速运动． （1）从初始至两棒达到速度相同的过程中，两棒的动量守恒，有 0 2mv mv= ． 根据能量守恒，整个过程中产生的总热量 222 00 11 1(2 )22 4Qmvmvmv=− = （2）设 ab 棒的速度为初速度的 3 4 时，cd 棒的速度为 v′，则由动量守恒可知 00 3 4mv m v mv′=+ ． 此时回路中感应电动势和感应电流分别为 0 3(),42 EEvvBlIR ′=− =． 此时 cd 棒所受的安培力 F=IBl，cd 棒的加速度 Fa m= ． 由以上各式可得 22 0 4 Blva mR= ． 答案： （1） 2 0 1 4 mv （2） 22 0 4 Blv mR 【例 6】 解析：MN 滑过的距离为 3 L 时，它与 bc 的接触点为 P，如图 4—9 所示．由几何关系可知，MP 的长度为 3 L ， MP 相当于电路中的电源，其感应电动势 1 3EBLv= ，内阻 1 3rR= ．等效电路如图 4—10 所示． 图 4—9 图 4—10 外电路并联电阻为 12 233 12 9 33 RRR × == + 并 由闭合电路欧姆定律可得，MP 中的电流 EI Rr= +并 ac 中的电流 2 3acI I= 联立以上各式解得 2 5ac BLvI R= 根据右手定则，MP 中的感应电流方向由 P 流向 M，所以电流 Iac 的方向由 a 流向 c． 答案： 2 5ac BLvI R= ，方向由 a 流向 c． 【例 7】 解析：（1）线圈中产生的热量应用转动过程中产生的交变电流的有效值来计算．因线圈中感应电动势的峰值 为 2 mENBaω= ，故线圈中电流的有效值为 2 22 2 mmIENBaI RR ω== = ，线圈转过 90°角经历的时间为 42 Tt π ω== ． 所以此过程中产生的热量 224 2 4 NBaQIRt R π ω== ． （3）线圈转过 90°角的过程中，感应电动势和感应电流的平均值分别为 22 222 2 NBa NBa E NBaEN ItRR ω ω π ππ ω ΔΦ=== ==Δ 所以通过导体截面的电量为 2NBaqIt R== 答案：（1） 224 4 NBaQ R π ω= （2） 2NBaq R= 【例 8】 解：（1）带电粒子在电容器两极板间静止时，受向上的电场力和向下的重力作用而平衡 1Umg q d= 求得电容器两极板间的电压： 14 1 15 110 100.01 1V 10 mgdU q − − ×××== = 由于粒子带负电，可知上极板电势高． 由于 S 断开，R1 上无电流，R2、R3 上电压等于 U1，电路中的感应电流． 即通过 R2、R3 的电流强度为： 1 1 23 1 0.1A82 UI RR===++ 由闭合电路欧姆定律可知：ab 切割磁感线运动产生的感应电动势为： 1UIrε = + ① 其中 r 为 ab 金属棒的电阻． 当闭合 S 后，带电粒子向下做匀加速运动，根据牛顿第二定律有： 2Umg q mad−= 求得 S 闭合后电容器两极板间的电压 14 2 15 ()10(107)0.010.3V 10 mg adU q − − −×−×== = 这时电路中的感应电流为： 2 2 2 0.3 0.15A2 UI R=== 根据闭合电路欧姆定律有： 13 22 13 ()RRI RrRRε =+++ ② 将已知量代入①②求得 1.2V 2rε ==Ω 又因： 1.2 3m/s0.4 1BLv U BL εε ====× ∴ 即金属棒做匀速运动的速度为 3m/s，电阻 r=2Ω． （2）S 闭合后，通过 ab 的电流 I2=0.15A，ab 所受安培力 F2=BLI=0.4×1×0.15=0.06N ab 以速度 v=3m/s 匀速运动时，所受外力必与安培力 F2 大小相等，方向相反，即 F=0.06N． 方向向右（与 v 同向），可见外力 F 的功率为：P=Fv=0.06×3=0.18W 【例 9】 解：依题意，电源端 3450% 0.5 2 1 10 10 5 0.5 5 10 WmghPQght ρ=×= ×=×××××=×输出 输出电压 U0=240V 为满足输电要求，由 2PIRΔ=损总 有： 46% 5100.06 10A30 PPI RR ×Δ ××== = =输出损 送 则送电电压为 4 3510 510V10 PU I ×== =×输送 送 送 所以升压变压器的变压比为 12 0 3 240 6125 510 nn UU ×送∶= ∶ = =∶ 输电线电压损失 10 30 300VUIRΔ= =×=损 送 用户端 3 1 5 10 V 300V 4700VUU U=−Δ=×− =损送 ，据题意可知 U2=220V 所以降压变压器的匝数比为 12 1 2 4700 235 11220nn UU′′∶=∶ = = ∶ 因为理想变压器没有能量损失，所以可正常发光的电灯的盏数为： 445 10 5 10 0.06 470100 PPN P −Δ ×−××== =损输 灯 （盏） 跟踪练习 1．D 提示： BFBlIBlStR Δ==Δ安 ． 2．（1）ab 或 cd 切割磁感线所产生的感应电动势为 Blvε = 对应的感应电流为 BlvI RR ε== ab 或 cd 所受的安培力为 22BlvFBIl R== 外力所做的功为 23 22BlvWFl R=×= 由能的转化和守恒定律，根据匀速拉出过程中所产生的焦耳热应与外力所做的功相等，即 23 2 BlvQW R== （2）令 0 BlvI R= ，画出的图象（答图 4—1）分为三段． 00 2230, ,0 ,llllltiItit iIvvvvv==−= == = （3）令 U0=Blv，画出的图象（答图 4—2）分为三段 0 0 0 0, 44 4 4 2 , 323 3 3 3, 44 4 4 ab ab ab UlRBlvtUvR lltUBlvUvv Ull R BlvtUvv R εε εε = =− × =− =− =− ==−=− = =− × =− =− =− 3．A 提示：当滑动头下移时，R3↓R 总↓， UI R= ，U 不变 I↑U 并=U－UR↓ 222 ARIR I I I↓=−↑ A2 的示数变大，由原副线圈电流与匝数成反比，可知 A1 的示数变大． 4．（1）电流方向由 N→M，ab 棒的速度先变大后变小．（2）在最低点，ab 切割磁感线产生的 E=BLv．瞬时功率： 2222 22 BLvP RR ε== ．（3）下滑过程中，设小电珠上产生的热量为 Q，则整个电路上产生的热量为 2Q 由能量守恒定律有： 22112, (2 )24mgr mv Q Q m gr v=+ = −∴ ． 5．金属杆从轨道上由静止滑下，经足够长时间后，速度达最大值 vm，此后金属杆做匀速运动，杆受重力、轨道的支持力和 i t O 答图 4—1 Uab t O l0 l0 － l v 2l v 3l v l v 2l v 3l v 0 /4U− 03/4U− 0U− 答图 4—2 安培力如答图 4—3 所示．安培力 mBLvF LBR= ，对金属杆列平衡方程 22 sin mBLvmg Rα = ， 则 22 sin m mg Rv BL α= ，由此式可知，B 增大，vm 减小；α 增大；vm 增大；R 变大，vm 变大；m 变小，vm 变小．因此 BC 两选项正确． 答案：BC 6．设杆向上运动的速度为 v，因杆的运动，两杆与导轨构成的回路的面积减小，从而磁通量也减少．由法拉第电磁感应定 律，回路中的感应电动势的大小 21()EBllv=− ① 回路中的电流 EI R= ② 电流沿顺时针方向．两金属杆都要受到安培力作用，作用于杆 x1y1 的安培力 11f Bl I= ③ 方向向上，作用于杆 x2y2 的安培力 22f Bl I= ④ 方向向下．当杆做匀速运动时,根据牛顿第二定律,有 12120Fmgmgf f− −+−=⑤ 由①②③④⑤得 12 21 () () F mmgI Bl l −+= − ⑥ 12 22 21 () () F mmgvR Bl l −+= − ⑦ 作用于两杆的重力的功率的大小 12()Pmmgv=+ ⑧ 电阻上的热功率 Q=I2R ⑨ 由⑥⑦⑧⑨式得 212 12 1222 2121 () ()() [ ]()() F m mg F m mgPRmmgQRBl lBl l −+ −+=+=−− 7．D 提示：小金属杯进入或离开磁场时，磁通量会发生变化，并产生感应电流，当小金属杯全部进入磁场后，不产生磁 感应电流，由能量守恒可得产生的焦耳热等于减少的机械能．即 2211()22Qmvmgbmgamgbamv=+−=−+ 8．由两表的量程和电阻 R 的大小可判定哪一个表满偏；由功能关系即可求出外力 F 的大小；撤去外力后，感应电流大小不 断变化， 平均作用力的冲量 BIL·△t=BLq=m·△v，变力作用下的导体运动问题可从电荷量的角度进行分析． 答案：（1）满偏的电表是电压表．因为若电流表满偏，电路中的电流 I=3A，电阻 R 两端的电压 U=IR=1.5V，已超过电 压表量程． （2）外力拉动金属棒匀速右移时，外力的功率全部转化为电路中的电功率．根据功能关系有 2 ()FvIRr=+ 而 UI R= ，所以 22 22 () (0.50.3) 0.5 2 URr IF Rv +×+== + N=1.6N （3）撤去外力 F 后，金属棒 CD 做减速运动，把金属棒减速至零的时间分成许多极短的时间间隔△t1、△t2、…、△tn， 在每一个极短的时间间隔内电流强度可以认为保持不变，大小分别为 I1、I2、…、In，由动量定理可得金属棒在整个时间内 的动量变化等于各段时间内所受安培力的冲量之和，即： 12 1122mv mv BILt BILtΔ+Δ + = Δ+ Δ+LL 即 mv=BLq 由电磁感应定律原来匀速右移的棒中产生的感应电动势 ()EBLvIRr= =+代入上式得 220.1 2 C0.25C()2(0.50.3) mvq IR r ×== =+×+ 9．当线圈中通过高频交变电流时，由于电磁感应，图形金属工件中产生的感应电动势大小为 2 100 2 sin (V)BBeSr ttt tπωΔΦ Δ Δ== = =ΔΔ Δ 其最大值 100 2VmE = ，则有效值 E=100V 工件非焊接部分的电阻 R1=R0·2π r，代入数据得，R1=2×10－3Ω 焊接部分的电阻 R2=99R1，根据串联电路的电压分配关系，R2 两端电压 2 12 RUERR= + 由 2UP R= 得，焊接处产生的热功率 22 2 2 2 12() REUP R RR == + ，代入数据解得 P=4.95×104W 10．（1）当 R0=30Ω时，R0 与 R2 的并联阻值为 02 02 RRR RR ′ = + =5Ω． 显然，这时电压表满偏，读数为 10V，电流表读数为 2A．（如果电流指针偏满，为 3A，则电压表上电压为 3×5=15（V）， 超过它的量程，不能安全使用） 在这种情况下电路中感应电流的总功率为 22 11 1()2(55)40PIRR′=+=×+=（W）． 根据能的转化和守恒定律，F1 的功率与感应电流的功率相等即为 40W． 由 111PFv= ，可知 ab 的速度 1 1 1 40 140 Pv F===（m/s）． （2）当 R0=3Ω时，它与 R2 的并联阻值 02 02 36 236 RRR RR ×′ ===++ （Ω）， 电路中总电阻 R=R′＋R1=7（Ω）， 显然，这时电流表指针满偏，为 3A，电压表示数为 6V．（若电压表指针满偏为 10V，则通过电流表的电流为 10 2 =5（A）， 超过它的量程不能安全使用．） 这时电路中感应电流的总功率，即 F2 的功率为 22 22 3763PIR= =×=（W）． ab 切割磁感线产生的感应电动势为 22237 21EBlvIR===×=（V）． （因 ab 的电阻不计） 在（1）问中，感应电动势为 1111()2(55)20EBlvIRR′== +=×+=（V）． 11 2 21 22 1 21,120 Ev EvvEv E===×=1.05（m/s） 由 222PFv= ，可得作用于 ab 的恒力为 2 2 2 63 601.05 PF v== =（N）． 11． B 简谐波形交流电有效值 1 2 A2I = ，方形波形交流电的有效值 I2=1A． 12．当自行车车轮转动时，通过摩擦小轮使发电机的线框在匀强磁场内转动，线框中产生一正弦交变电动势，其最大值 0mENBSω= ，式中 0ω 为线框转动的角速度，即摩擦小轮转动的角速度． 发电机两端电压的有效值 2 2 mUE= 设自行车车轮转动的角速度为 1ω ，由于自行车车轮与摩擦小轮之间无相对滑动，则 11 0 0Rrω ω= 小齿轮转动的角速度与自行车轮转动的角速度相同，也为 1ω ．设大齿轮转动的角速度为ω ，则 321RRω ω= ．由以上各式解得 20 31 2 RrU BSN R Rω = 代入数据得ω =3.2rad/s 13．A 14．（1）S 闭合后，电流由 a 到 b 通过直导线，电流大小为 0 EI RR ′= ′+ =0.5（A） ab 开始运动（速度为零）时的加速度为 0 0 1.0 0.5 0.5 50.05 BlIa m ××== =（m/s2）方向水平向右． 当 ab 运动速度为 v（方向向右）时，感应电动势大小为 E=BLv，这时通过 ab 的电流（仍由 a 到 b）为 EEEBLvI RR RR ′′−−==′′++ 可见，ab 的运动速度增大时 I 减小，ab 所受安培力、加速度也随之减小；当 I 减小至零时，ab 所受安培力、加速度为 零．这时，ab 速度最大，最大速度为 6 121.0 0.5m Ev Bl ′== =× （m/s） （2）S 刚闭合时，由于惯性原因 ab 速度仍为零，电容器两极板间电压为 00 0.5 3UIR′= =×=1.5（V） ab 以最大速度 vm=12m/s 运动时，电路中电流为零，电容器两极板间电压为 mUE Blv′= = =6（V） 可见，电容器的带电荷量在 ab 由开始运动到达到最大速度的过程中增加了 66 0()210(61.5)9.010QCUU −−Δ= − =× × − = × （C） 15．A 提示：A 图中 ac 段电阻上无电压降，Uab=Ucd，其他正确． 16．在输送功率一定的情况下，可以求出送电电流，由损失功率可求出输电线中的电阻．根据题目要求，由损失功率计算 出输送电压． （1）P 输=UI 线，所以 500 6 PI U==输 线 A 4800 20024P ==损 kW 因 2PIR=损 线线 故 2 28.8PP I ==损 线 线 Ω （2）若 P 损=500kW×2.304%=11.52kW 故送电电流 20PI P==损 线 线 A，送电电压 42.5 10PU I==×送 线 V． 专题五 物理实验参考答案 典型例题 【例 1】 解析： （1）利用逐差法求小车的加速度．由纸带可知，任意两相邻记数点间的时间间隔 T=0.04s， 由逐差法可得 61 72 83 94 12 3 42222,,, 5555 SS SS SS SSaa a a TTTT −−−−==== 则 1234 61 7 2 83 94 2224 1 ()445555 aaaa S S S S SS S Sa TTTT +++ − − − −==+++ 6789 1234 2 2 2 ()() 20 (8.33 8.95 9.16 10.26) (5.12 5.75 6.41 7.05) 10 m/s 20 (0.04) SSSS SSSS T − +++ − +++= +++ − +++=× × =4.00m/s2 （2）为了求出小车下滑过程中所受到的阻力， 还需要测量小车的质量 m，斜面上任 意两点间距离 l 和这两点间的高度差 h．　 小车的受力情况如图 5—2 所示．根据牛顿第二定 律，　 sin ,mg f maθ −= 而 图 5—2 sin h lθ = 所以， hf mg mal=−． 【点评】 （1）逐差法充分利用了纸带的实验数据，从而减小了数据测量引起的偶然误差．本题中所给出的实验数据 个数为奇数（9 个），处理时常舍掉正中间的一个数据．　 （2）小车下滑过程中所受到的阻力无法直接测量，但根据牛顿第二定律可转化为测量 m，a，h 和 l．与此相类似，你 能求出打点计时器打纸带上的两记数点的过程中小车克服阻力所做的功吗？ 【例 2】 解析： ①本实验测量角速度的原理是：圆盘匀速转动时，其线速度 sv t= ，又角速度 v rω = ，所以，其原理 式为 s rtω = ．　 在纸带上选定两点，设它们在米尺上对应的刻度值分别为 x1、x2，数出这两点间（含这两点）的打点数 n，打点计时器 打点的周期为 T，则打这两点的时间间隔 t=(n－1)T，这段时间内圆盘转过的弧长 S=x2－x1，若测得圆盘的半径为 r，由已知 量和测得量表示的角速度的表达式为 21 (1) x x Tn rω −= − ． ②若取 120, 6xx==cm，则 n=9，又 21 s, 5.50 1050Tr −==×cm． 代入可得 2 2 6.0 10 rad/s 6.8rad/s1 85.01050 ω − − ×== ×× × 【点评】 实验原理是完成实验的依据和关键．虽然该实验没有做过，但所用到的实验方法并不陌生，要结合题给实验 器材和实验步骤通过联想和迁移，弄清实验原理和所需测量的物理量，进而得出待测量的表达式． 【例 3】 解析： （1）由于小灯泡灯丝的电阻值远小于电压表的内阻（如：电压为 2.00V 时，其阻值 R 灯 = 2.00 4.000.50 U I =Ω=Ω），为减少由于电表接入电路引起的系统误差，应采用电流表外接法．为使小灯泡两端的电压的变 化范围尽可能大，滑线变阻器应连接成分压电路，实验电路如图 5—6 所示．　 图 5—6 图 5—7 　　 （2）根据实验得到的数据在 U—I 坐标系中描点，并将这些数据点连接成一条平滑的曲线，如图 5—7 所示．　 （3）根据 1.5 2UEIr I=−= − 作出电源的 U—I 图线，它与小灯泡的伏安特性曲线的交点坐标就是小灯泡的工作点， 即工作电流 I=0.35A，工作电压 U=0.08V，故小灯泡的实际功率 P=IU=0.28W． 【点评】 本题主要考查独立完成实验的能力．主要包括①实验原理及电路；②用图象法．．．处理实验数据，并得出实验结 论．其中利用图线确定小灯泡与电源连接后的工作点是解答本题第（3）问的关键．　 【例 4】 解析：本实验测定小铁块克服摩擦力所做功的原理是动能定理和平抛运动的规律。 小铁块自斜面顶端由静止下滑到底端的过程中，根据动能定理 21 2fmgH W mv−= …………①　 离开曲面后，小铁块做平抛运动，直到落地， 则 21 2hgtSvt== 所以， 2 gvS h= …………②　 将②代入①得 2 4f mgSWmgH h=− 显然，实验中需要测量的物理量是：斜面 高度 H、桌面高度 h，小铁块平抛的水 平距离 S、小铁块质量 m．如图 5—9 所示，其中 S 需用重锤线和白纸、复写纸来确定． 【答案】 （1）重锤线、铺在地面上的白纸和复写纸 （2）斜面高度 H、桌面高度 h，小铁块平抛的水平距离 S，小 铁块质量 m （3） 2 4f mgSWmgH h=− 【点评】 题给实验器材对实验原理的设计有一定的限制作用．本题没有给足实验器材，首先要根据题给实验条件和要 求，构思相关的物理情景．．．．，从而确定实验原理，然后根据原理式确定需要测量的物理量和还需选用的实验器材．　 【例 5】 解析：（1）器材选择（测量电路） 从减小电表读数引起的偶然误差的角度考虑，两电表及电表与电源间的配置要合理．注意到电源电动势远小于电压表 V2 的量程，而跟电压表 V1 的量程较接近，若选用电压表 V2 来测量电压，其最大偏转量达不到量程的 1 3 ，读数时偶然误差 太大，所以选用 V1 较恰当； 而此时通过电流表的最大电流 4 10 A400A 2.5 10 m m x UI R μ== = × ，因此，电流表 A2 与 V1 配置 较好．　 （2）电路选择（控制电路）　 电路选择主要从滑动变阻器对电路的控制和调 节的角度考虑．若采用限流电路控制， 注意到测量部分的总电阻约为 20kΩ，远大于滑动 变阻器的总电阻（1kΩ），要保证电 表安全，变阻器分得的电压至少为 5V，阻值应调到 10kΩ，显然，限流不能起到保证电表 安全的作用，更不能进行有效调节，所以，只能采 用分压电路控制，实验电路如图 5— 10 所示．　 【点评】 伏安法是测量电阻的一种最基本方 法，其原理是部分电路欧姆定律，原 理式为 x UR I= ．分析这类问题的关键是从电表配 置要合理选择器材，从对电路的控制 和调节选择控制电路．并联分流和串联分压原理是伏安法测电阻原理的迁移和延伸，下例是这类问题的变式． 变式：【点拨】 （1）本题中测量电阻的原理是并联分流或串联分压．由于滑动变阻器的最大阻值远小于测量部分的阻 值，且电源电动势大于两电压表的量程，在调节滑动变阻器的过程中，为保证电压表的安全，且其读数有明显的改变，滑动 变阻器应采用分压式控制电路，电路原理图如图 5—12 甲或乙所示．　 图 5—12 图 5—9 图 5—10 （2）实物连线如图 5—13 甲或乙所示　 图 5—13 （3）若采用甲电路，根据并联电路的电流分配关系， 211 21x UUU rrR=+ 解得 112 21 12 x UrrR Ur Ur= − ．　 若采用乙电路，根据串联电路的电压分配关系， 121 1 UUU rR −= 解得 21 1 1 () x UURrU −= ．　 【点评】 本题主要考查电阻测量的原理、电路设计、实物连线等知识，测试设计简单实验方案的能力．①对于内阻已 知的电压表，可作电流表使用．使用电表时，必须考虑电表间的量程配置，本题要求电压表读数不小于量程的 1 3 ，因此， 电压表 V2 与 V1 的位置不能互换．②进行实物连线时，应注意以下几个问题：a．直流电表的正、负接线柱（正接线柱应连 接在电路电势高端，负接线柱应连接在电路电势低端）；b．电表的内外接法；c．滑动变阻器的接法（限流或分压，接通电 路后，应使电表读数最小）；d．开关的连接（应在干路上，闭合前电表读数为零）．　 【例 6】 解析： （1）实物连线如图 5—17 所示．　 （2）电阻箱的阻值 R1=0×100Ω＋8×10Ω＋6×1Ω＋3×0.1Ω=86.3Ω． 本题测量电流表的内阻的方法是“替代法”．即用电阻箱的阻值替代电流表 A1 的内阻值，其条件是：开关 S2 分别扳到 a 处和 b 处时，保持滑动变阻器 R2 不变，且使电流表 A2 读数相同．所以，待测电流表 A1 的内阻 1 1 86.3ARR== Ω． 图 5—17 （3）当 R2 调为零时，要使电路中的电流 I 不超过电流表 A2 的量程，根据闭合电路欧姆定律可知，电路总电阻 R 总至少 为： 2 4 6 4 210 200 10A ER I −== =× ×总 Ω=20kΩ．由于电流表 A1、A2 的内阻（约为 100Ω）远小于 R 总,故保护电阻 R3 应选 用 20kΩ的电阻，但若选用 200kΩ的电阻，则电路中电流太小，电流表 A1、A2 指针偏转量太小，读数不明显，实验误差太 大．所以,正确的选项为 B． （4）由于 R3=20kΩ，调整滑动变阻器 R2 时，要使电流表 A2 的读数为 150 Aμ ，则 2 ER I≈ －R3= 6 4 150 10−× Ω－2× 104Ω≈7kΩ．若选用 1kΩ或 5kΩ滑动变阻器，则不能满足实验要求（A2 读数为 150 Aμ ）；若选用 25kΩ的滑动变阻器， 则调节范围太小（不方便调节），所以，选用 10kΩ的滑动变阻器较合适，正确的选项为 C． 【点评】 实验条件的控制是高考考查的重点之一．保护电阻和滑动变阻器在电路中起着控制和调节的作用，选用时应 根据实验条件和要求进行优选，既要保证电表安全(不能太小)，又要方便调节(不能太大)． 【例 7】 解析： （1） 用此电路测量表头内阻的方法是半偏法． S2 断开和 S2 闭合的两次操作中要求干路电流（Ig） 近似不变，而满足这个条件必须使滑动变阻器 R 的阻值远大于 Rg，因此滑动变阻器应选用 R2．而 2 g EI R≈ ，显然 E 越大， R2 越大，实验条件满足得越好，误差越小，所以，电池应选用 E3．　 （2）图 5—18（乙）所示的电路较合理，因为图（丙）电路在通电状态下，更换量程时会造成两个分流电阻都未并联 在表头两端，以致通过表头的电流超过其满偏电流而损坏．　 （3）核对电路如图 5—19 所示．为使改装后 的电流表与标准表在 0～1mA 之 间逐格核对，应选用分压电路．由于○A 和 A′ 满 偏电流和满偏电压都很小，为使滑 动变阻器便于调节，即有较大的调节范围，滑动变 阻器应选用 R1，电池应选用 E1， 且在电流表所在的支路上串联定值电阻 R0，起保护 作用． 【点评】 测量电阻的方法很多（包括伏安法、 替代法、半偏法等），但其原理总 是部分电路欧姆定律或闭合电路欧姆定律．在具体 问题中，选用哪种测量方法应根据 所提供的实验器材和实验要求来确定． 【特别提示】 1．半偏法测电阻的实验中，实 验条件的控制直接影响测量精确 度．　 2．在分压电路中，为使实验便于调节，应选用全电阻较小的滑动变阻器． 【例 8】 解析： （1）①实物连线如图 5—21 所示，为了使改装表与标准表在零到量程的范围内一一校对，应采用分 压电路．　 ②根据串联电路的电压分配关系，有 0 1.0 3.0 1.0 1000 R −= 解得 R0=2000Ω （2）①先将电压表 VC 通过开关、导线与电源连接， 读出 VC 上的示数 UC；再将电压 表 VC 和 VB 串联，通过开关、导线与电源连接，读出 VC 上的示数 UC′和 VB 上的示数 UB． ②根据上述两步操作可得 C CC U E RRr= + ①　 CB CB CB UU E RR R Rr ′ + =+++ ②　 B BC C URRU= ′ ③　 由①②③三式解得 3000CBC CC UUUr UU ′ +−=×′− Ω 【点评】 本题综合考查了电表改装、电表校准电路及测量电源内阻的方法，测试设计和完成实验的能力．用电压表 VB 和 VC 测量电源的内阻时，应注意： 尽管两电压表的量程相同，但其内阻并不一定相同(表头可能不同)．　 图 5—19 图 5—21 跟踪练习 1．DGH 　　 2．甲 50分度的游标卡尺的精度为 1 5 mm=0.02mm，因此，读数的最后一位数字应是“2”的整数倍或“0”． 3．2.40 比较甲、乙两图可知，甲图中弹力大于滑动摩擦力，铁块 P 做匀加速直线运动;乙图中铁块 P 处于平衡状态，弹力 大小等于滑动摩擦力大小．　 4．1．6 考察平抛物体的水平分运动，结合图给数据可知，两段时间之比为 2︰1，若 O 点是平抛的起点，则竖直分位移 y1︰y2= 2211(2 ) (3 )22g tgtΔΔ∶ =4︰9，所以，O 点是平抛的起点．根据平抛运动的规律，有 32.0×10－2=v0t，19.6×10－2= 21 2 gt ， 联立解得 v0=1.6m/s 　　 5．（1）0.97m/s （2）0．48J （3）0．47J 　（3）重锤下落过程中受到阻力及纸带受到打点计时器的阻力作用，重锤 的机械能减小．　 6．B A 电压表量程过大，读数误差太大 A B 变阻器阻值太大，额定电流太小，调节时电表读数变化不明显． 7． B　 点拨：由热敏电阻的 I—U 图线知，工作电流 I=40mA 时，电压 U=5.6V，则此时加在电流表两端电压为(9－5.6)V=3.4V， 所以 3 3.4 85 40 10AR −=Ω=Ω × ． 8．（1）AB 100Ω （2）AC A 90Ω 10kΩ　　 9．1.630 360 　 10．在白纸上另画一条与 y 轴正方向的夹角较小的直线 OA，把大头针 P1、P2 竖直的插在所画的直线上，直到在 y<0 的区域 内透过玻璃砖能看到 P1、P2 的像，插上 P3 后，P3 刚好能够挡住 P1、P2 的像． sin sinn β α= ． 11．（1）110 （2）8×10－6 （3）7×10－10 12．0.9906，100.40， 22 2 4nL t π 13．（1）0．420 0．417 （2）①0.05N ②BC 14．应测量的物理量有：小物块的质量 m，两小物块的落地点之间的距离 S，桌面的高度 h，桌面的长度 d．　 2() 8p mg S dE h −= 15．实验步骤：（1）将 S1 闭合，S2 断开,电压表直接和电源相连，记下电压表读数 U，就是电源的电动势;（2）S1、S2 均闭 合，记下电压表读数 U2，即为电阻 R 两端电压．　 根据闭合电路欧姆定律，有 2 2 UEU rR=+ ， 即 2 12 UUU rR=+ ，解得 12 2 UUrRU −= 16．（1） 2 4 xdR l π （2）36.48～36.52 0.796～0.799 （3） 12 12 x UUR I I== 17．（1）如图 5—46 所示 （2）增大，17Ω 18．（1）首先来分析电路的测量部分．由于电流表 A2 量程与待测电流表 A1 量程相差太 大，从实验测量精度考虑，不能直接将电流表 A2 与电流表 A1 串联来测量电流．注意到 电压表内阻已知，而允许通过电压表的最大电流为 3 3V 1000 A 310 μ= ×Ω ，跟待测电流表 的量程接近，因此，可将电压表与电流表 A1 串联， 利用其读数来计算通过电流表 A1 的电 图 5—46 流．　 再来分析电路的控制部分．若将滑动变阻器接成限流式，则通过待测电流表的最小电流大约为 3 3V 750 A (3 1) 10 μ= +× Ω ， 显然，不能保证电表安全,也无法通过调节测量多组数据．因此，应采用分压式控制电路，为了便于调节，应选用最大阻值 20Ω的滑动变阻器．　 综合以上分析，选用的器材应为 A、C、D、F、 G 其实验电路如图 5—47 所示．　 （2）实验过程中，调节滑动变阻器滑动触头，使 待测电流表 A1 的指针偏转 n 格，读 出此时电压表 V 的示数 U，则通过待测电流表的电流 V UI R= 由此可得,电流表的满偏电 流 max V NNUIInnR== ，式中 U 为电压表的读数， RV 为电压表的内阻． 19．（1）如图 5—48 所示　 （2）A1、A2 两电流表的读数 I1、I2 和电阻箱 R1 的阻值 12 12 1 2 , IIRr RI −= ． 图 5—48 图 5—49 图 5—50 20．（1）连接线路如图 5—49 所示．　 （2）把变阻器的滑动触头移到靠近 D 端处．调节 R，使电压表读数为 6V．记下电压表读数，在导电纸上移动探针， 找出电压表读数与所记下的数值相同的另一点． 21．（1）R1 （2） 电路如图 5—50 所示 （3）1.4 8，0.8 　 22．（1）当电压○mA 满偏时，通过其电流 UI R==1mA，故电流表选 1.5mA 量程．　 若合上 S 后， 3 mV 3 150 10 V 1.05 10 A UR I − − ×== × =143Ω．　　 （2）可把电压表○mA 当成量程为 150mV、Rg=143Ω表头处理，其改装后量程为 10mA，则通过○mA 的满偏电流为 3150 10 V 143 g g g U I R −×== Ω =1.05mA． 由部分电路欧姆定律知 3 3 150 10 V (10 10.5) 10g UR I − − ×== −× =16.8Ω．　　 　 ○A 量程选 15mA．　 图 5—47 图 5—51 图 5—52 23．（1）乙；D、E；大于 （2）如图 5—52 所示．　 24．（1）如图 5—53 所示　 （2）合上开关 S，调节电阻箱阻值，使电压表指针在中央刻度处，记下电阻箱的阻值 R1；再调节电阻箱电阻，便电压 表指针指在满偏刻度处，记下电阻箱的阻值 R2．　 V2 12RR R=− （或 22 11 V 12 UR URR UU −= − ） 　 　　 图 5—53