人教版小学六年级数学下册圆锥的体积

人教版小学六年级数学下册圆锥的体积

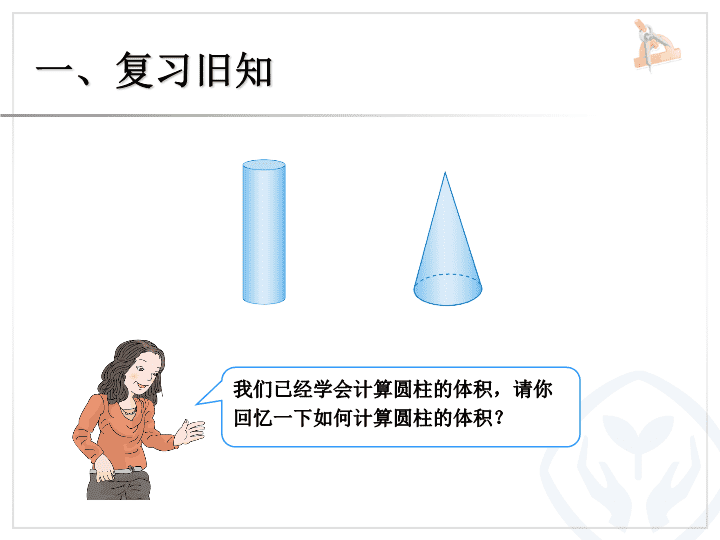
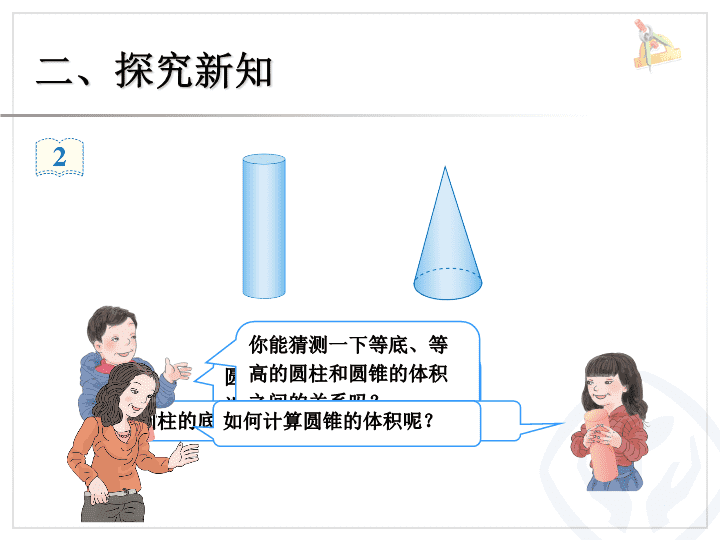
圆锥的体积 （例 2 、例 3 ） 圆柱与圆锥 一、复习旧知 我们已经学会计算圆柱的体积， 请你回忆一下如何计算圆柱的体积？ 二、探究新知 圆锥的体积与圆柱的体积有没有关系呢？ 你能猜测一下等底、等高的圆柱和圆锥的体积之间的关系吗？ 圆柱的底面是圆，圆锥的底面也是圆。 如何计算圆锥的体积呢？ （ 1 ） 各组准备好等底、等高的圆柱、圆锥形容器。 （ 2 ） 用倒沙子或水的方法试一试。 二、探究新知 下面就让我们通过实验，探究一下圆锥与圆柱体积之间的关系。 （ 3 ） 通过实验，你发现圆锥的体积与同它等底、等高的 圆柱的体积之间的关系了吗？ V 圆锥 ＝ V 圆柱 ＝ 3 1 3 1 Sh 二、探究新知 三次正好装满。 我把圆柱装满水，再往圆锥里倒。 正好倒了三次。 4 m 1.2 m （ 2 ）沙堆的体积： （ 1 ）沙堆底面积： 5.02 × 1.5 ＝ 7.53 （ t ） （ 3 ）沙堆重： 答：这堆沙子大约重 7.53 吨。 × 12.56 × 1.2 ＝ 5.024 ≈ 5.02 （ m ³ ） 3 1 3.14 × （ ） ＝ 3.14 × 4 ＝ 12.56 （ m 2 ） 2 4 2 就要先求出这堆沙的体积，也就是圆锥的体积。 要求出这堆沙子大约重多少吨，就要先求什么？ 工地上有一堆沙子，近似于一个圆锥（如下图）。这堆沙子的体积大约是多少？如果每立方米沙子重 1.5 t ，这堆沙子大约重多少吨？（得数保留两位小数。） 二、探究新知 （一）做一做 1. 一个圆锥形的零件，底面积是 19 cm 2 ，高是 12 cm ， 这个零件的体积是多少？ 三、知识应用 答：这个零件的体积是 76 cm ³ 。 × 19 ×12 ＝ 76 （ cm ³ ） 3 1 2. 一个用钢铸造成的圆锥形铅锤，底面直径是 4 cm ， 高 5 cm 。每立方厘米钢大约重 7.8 g 。这个铅锤重 多少克？（得数保留整数） 三、知识应用 （一）做一做 3 1 （ 2 ） 铅锤 的体积： （ 1 ）铅锤底面积： 21 × 7.8 ≈ 163 （ g ） （ 3 ）铅锤的 质量 ： 答： 这个铅锤 大约重 163 克 。 × 12.56 × 5 ≈ 21 （ cm 3 ） 3.14 × （ ） ＝ 3.14 × 4 ＝ 12.56 （ cm 2 ） 2 4 2 （二）解决问题 1. 填空 （ 1 ）一个圆柱的体积是 75.36 m ³ , 与它等底等高的圆锥的体积是（ ） m ³ 。 25.12 （ 2 ）一个圆锥的体积是 141.3 m ³ , 与它等底等高的圆柱的体积是（ ） m ³ 。 423.9 141.3 × 3 ＝ 423.9 （ m ³ ） 三、知识应用 75.36 × ＝ 25.12 （ m ³ ） 3 1 2. 一个圆柱与一个圆锥的底面积和体积分别相等。 已知圆柱的高是 4 dm ，圆锥的高是多少？ 4 × 3 ＝ 12 （ dm ） 答：圆锥的高是 12 dm 。 三、知识应用 想一想，当一个圆柱与一个圆锥的底面积和体积分别相等时，圆锥的高与圆柱的高又是什么关系呢？ 3. 一个圆锥形沙堆，底面积是 28.26 m 2 ， 高是 2.5 m 。用这堆 沙在 10 m 宽的公路上铺 2 cm 厚的路面，能铺多少米？ 三、知识应用 2 cm ＝ 0.02 m （ 1 ）沙堆的体积： ＝ 9.42 × 2.5 ＝ 23.55 （ m ³ ） 23.55 ÷ 10 ÷ 0.02 ＝ 2.355 ÷ 0.02 ＝ 117.75 （ m ） （ 2 ）所铺公路的长度 答：能铺 117.75 m 。 × 28.26 × 2.5 3 1 请你想一想，转换前后沙子的体积是否发生变化？ 转换前后沙子的体积不变，所以铺成的公路路面的体积等于圆锥形沙堆的体积。 作业：第 35 页练习六，第 7 题。 第 36 页练习六，第 8 题。 四、布置作业