人教版5年级下数学教学课件：探索图形

人教版5年级下数学教学课件：探索图形

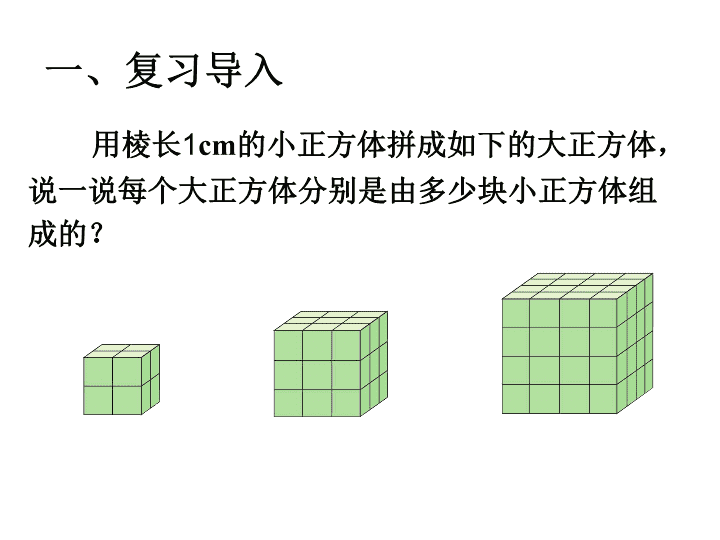
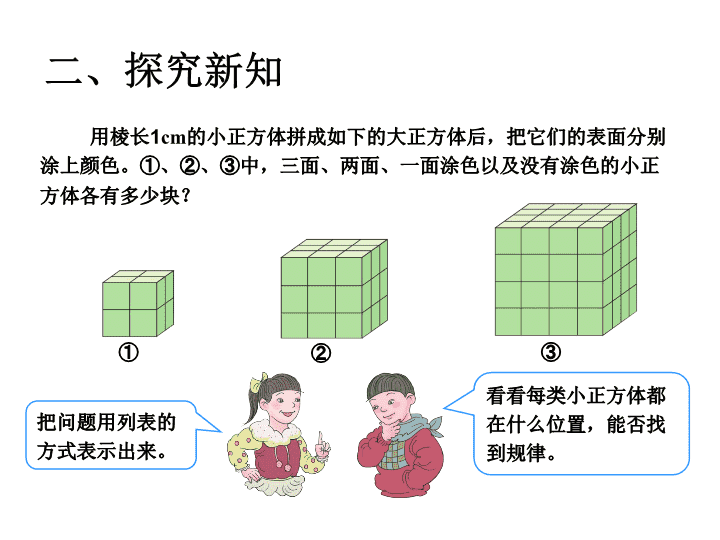
探索图形 用棱长 1 cm 的小正方体拼成如下的大正方体， 说一说每个大正方体分别是由多少块小正方体组 成的？    一、复习导入 用棱长 1 cm 的小正方体拼成如下的大正方体后，把它们的表面分别涂上颜色。 ① 、 ② 、 ③ 中，三面、两面、一面涂色以及没有涂色的小正方体各有多少块？ ① ② ③ 二、探究新知 把问题用列表的方式表示出来。 看看每类小正方体都在什么位置，能否找到规律。 用棱长 1 cm 的小正方体拼成如下的大正方体后，把它们的表面分别涂上颜色。 ① 、 ② 、 ③ 中，三面、两面、一面涂色以及没有涂色的小正方体各有多少块？ 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数  8 0 0 0  8 12 6 1  8 24   24 8 8 36 54 27 8 48 96 64 按这样的规律摆下去，第 ④ 、 ⑤ 个正方体的结果会 是怎样的呢？ 二、探究新知 ① ② ③ ① ② ③ ④ ⑤ 二、探究新知 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数  8 0 0 0  8 12 6 1  8 24   24 8 8 36 54 27 8 48 96 64 ① ② ③ ④ ⑤ 观察上表，你能发现什么？ 在顶点位置的正方体露出 3 个面，三面涂色的块数与顶点数相同，无论是哪一种正方体都是 8 个。 二、探究新知 观察上表，你能发现什么？ 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数  8 0 0 0  8 12 6 1  8 24   24 8 8 36 54 27 8 48 96 64 ① ② ③ ④ ⑤ 在每条棱中间位置的正方体露出 2 个面，两面涂色的块数与棱有关，即 （ n － 2 ） × 12 。 二、探究新知 观察上表，你能发现什么？ 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数  8 0 0 0  8 12 6 1  8 24   24 8 8 36 54 27 8 48 96 64 ① ② ③ ④ ⑤ 在每个面中间位置的正方体露出 1 个面，一面涂色的块数与面有关，即 （ n － 2 ） × （ n － 2 ） × 6 。 你能继续写出第 ⑥ 、 ⑦ 、 ⑧ 个大正方体中 4 类小正方体的块数吗？    三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数  8 0 0 0  8 12 6 1  8 24      24 8 8 36 54 27 8 48 96 64 8 60 150 125 8 72 216 216 8 84 294 343 三、知识运用 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ 四、布置作业 如果摆成下面的几何体，你会数吗？ 4 10 20