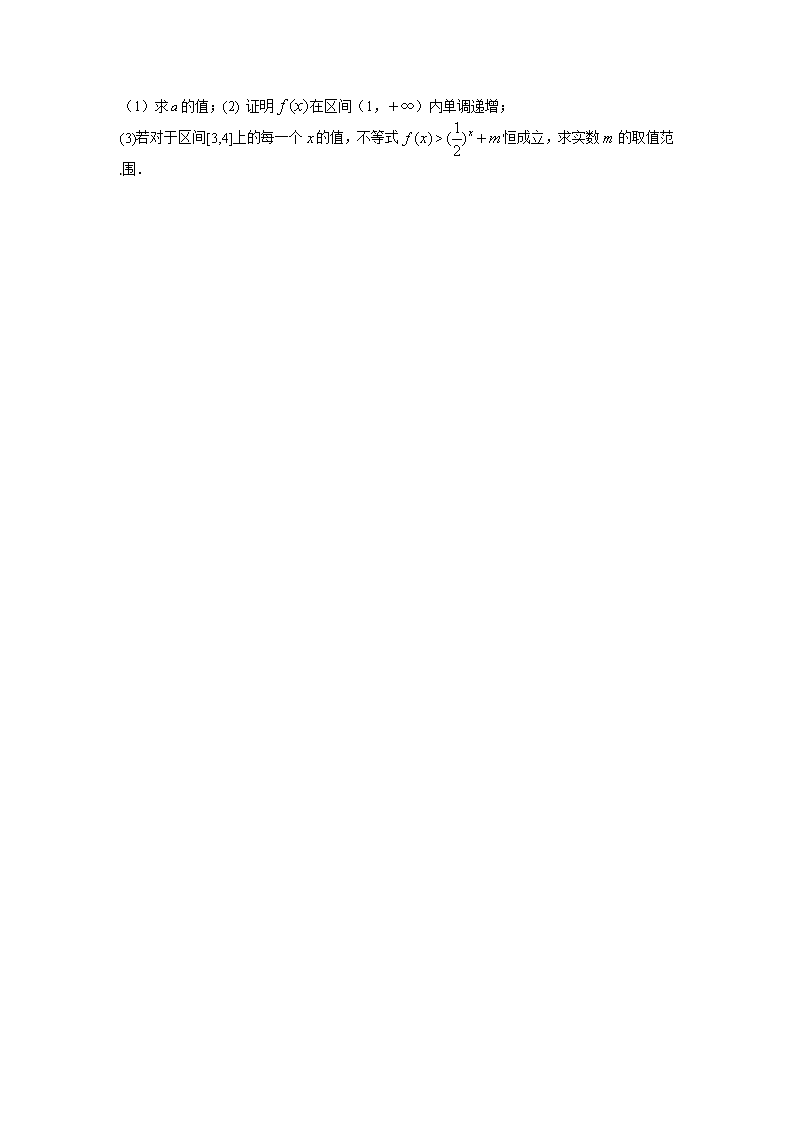吉林省长春二中2012-2013学年高一上学期期末考试数学试题
2012~2013学年第一学期高一期末考试数学试题
一. 选择题(每个题答案是唯一的,请把你认为正确的答案填在答题卡的表格内,每题4分,共48分)
1. 已知A={x︱-1,B={x︱},全集U=R,则=( )
A.{x︱
c>b B.a>b>c
C.c>a>b D.b>c>a
7. 函数的最小正周期为( )
A. B.π C.2π D.4π
8.若函数( )
A. B. C.15 D.
9. 将函数的图像左移,再将图像上各点横坐标压缩到原来的,则所得到的图象的解析式为( )
A B C D
10. 若| , 且()⊥ ,则与的夹角是 ( )
A. B. C. D.
11根据表格中的数据,可以判断方程ex-x-2=0必有一个根在区间( )
x
-1
0
1
2
3
ex
0.37
1
2.78
7.39
20.09
x+2
1
2
3
4
5
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
12.设为( )
A.(2,14) B. C. D.(2,8)
二、填空(每空4分共16分)
13.,则x=
14.=
15. 函数y=的定义域是
16. 已知△ABC为等边三角形,,设点P,Q满足,,,若,则
三、解答题(56分)
17.(8分)已知A=,求实数.
18. (8分)已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的 一段图象(如图)所示.
①求函数的解析式;
②求这个函数的单调增区间
19.(10分)已知
求(1)的范围;(2)若。
20.(10分)设向量,函数.
(Ⅰ)求函数的最大值与最小正周期;
(Ⅱ)求使不等式成立的的取值范围.
21. (10分)设f(x)是定义在(0,)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1求:(1)f(1);
(2)若f(x)+f(x-8)≤2,求x的取值范围。
22.(10分)设为奇函数,为常数.
(1)求的值;(2) 证明在区间(1,+∞)内单调递增;
(3)若对于区间[3,4]上的每一个的值,不等式>恒成立,求实数的取值范围.
21.解:(1)∵,∴f(1)=0。
(2),从而有f(x)+f(x-8)≤f(9),
即,∵f(x)是(0,+∞)上的增函数,故
,解之得:8<x≤9。
22. (1)∵ f(-x)=-f(x),∴.
∴ ,即,∴a=-1.
(2)由(1)可知f(x)=(x>1) 记u(x)=1+,
由定义可证明u(x)在(1,+∞)上为减函数, ∴ f(x)=在(1,+∞)上为增函数.
(3)设g(x)=-.则g(x)在[3,4]上为增函数. ∴g(x)>m对x∈[3,4]恒成立,∴m
查看更多