- 2021-06-19 发布 |
- 37.5 KB |
- 8页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学上册 第二十三章 旋转章末检测题(A)(新版)新人教版
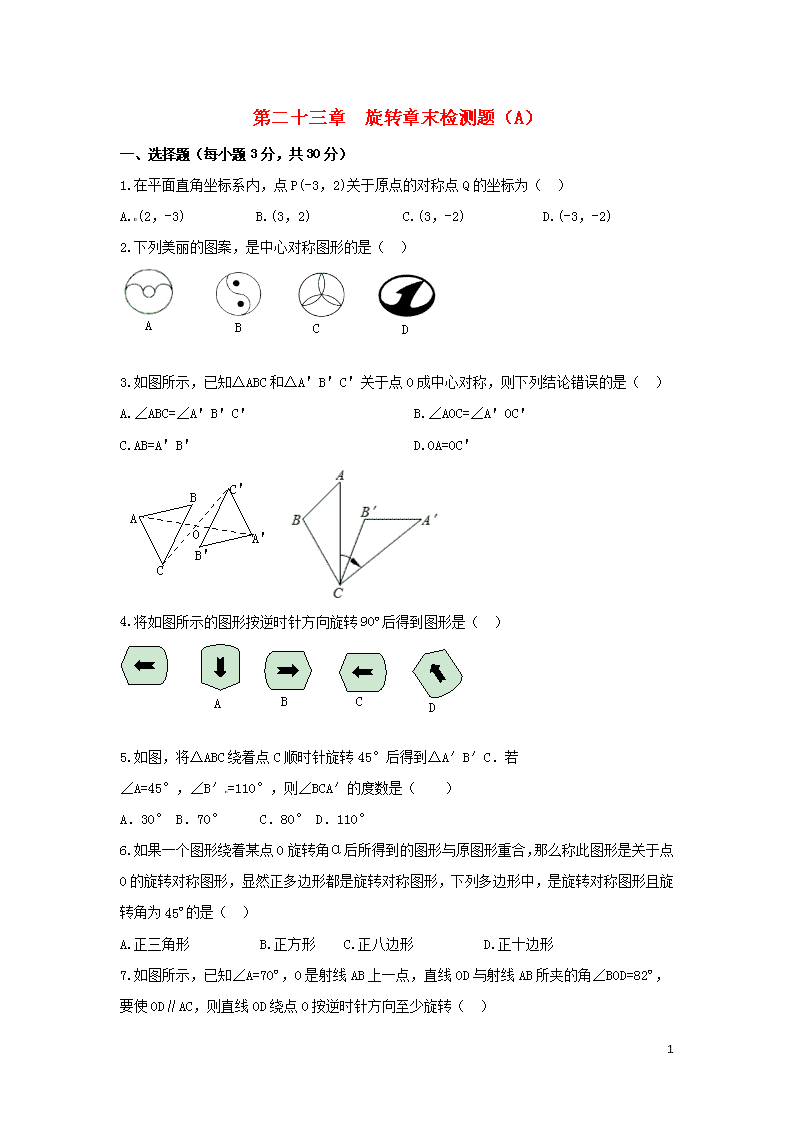
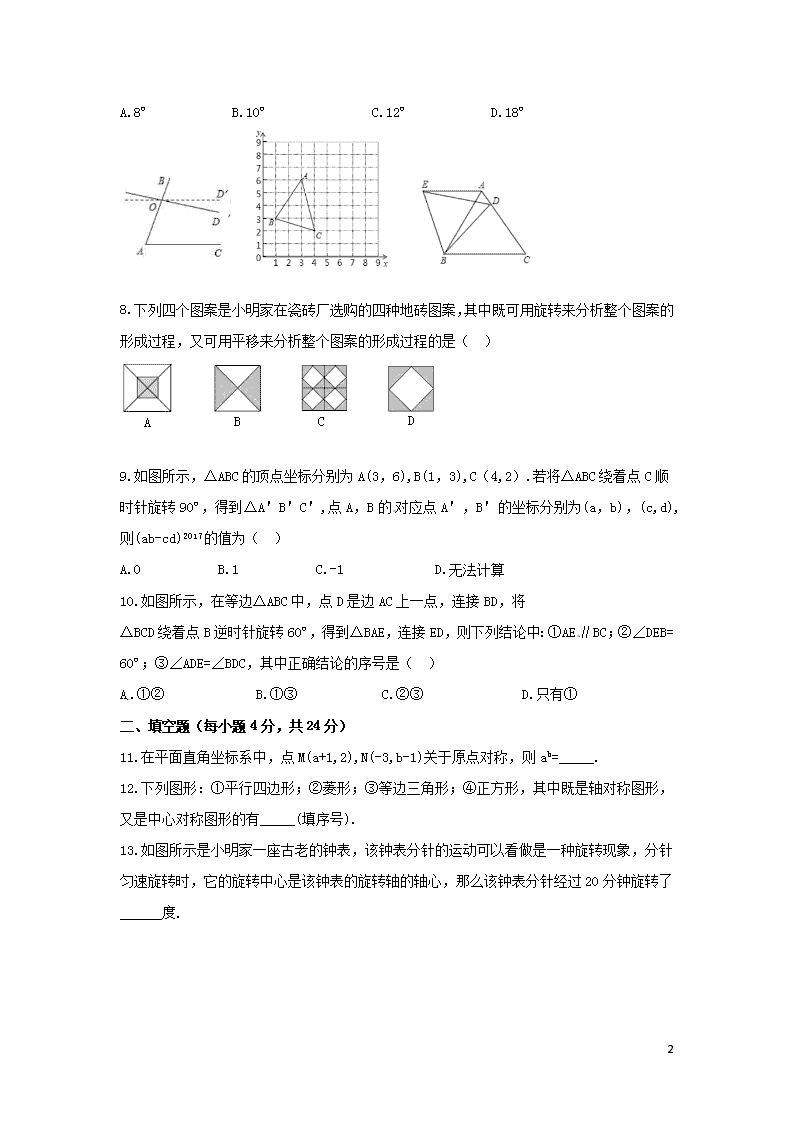
第二十三章 旋转章末检测题(A) 一、选择题(每小题3分,共30分) 1.在平面直角坐标系内,点P(-3,2)关于原点的对称点Q的坐标为( ) A.(2,-3) B.(3,2) C.(3,-2) D.(-3,-2) 2.下列美丽的图案,是中心对称图形的是( ) A D C B 3.如图所示,已知△ABC和△A'B'C'关于点O成中心对称,则下列结论错误的是( ) A.∠ABC=∠A'B'C' B.∠AOC=∠A'OC' C.AB=A'B' D.OA=OC' A B' C O C' B A' 4.将如图所示的图形按逆时针方向旋转90º后得到图形是( ) D C B A 5. 如图,将△ABC绕着点C顺时针旋转45°后得到△A′B′C.若 ∠A=45°,∠B′=110°,则∠BCA′的度数是( ) A.30° B.70° C.80° D.110° 6.如果一个图形绕着某点O旋转角α后所得到的图形与原图形重合,那么称此图形是关于点O的旋转对称图形,显然正多边形都是旋转对称图形,下列多边形中,是旋转对称图形且旋转角为45º的是( ) A.正三角形 B.正方形 C.正八边形 D.正十边形 7.如图所示,已知∠A=70º,O是射线AB上一点,直线OD与射线AB所夹的角∠BOD=82º,要使OD∥AC,则直线OD绕点O按逆时针方向至少旋转( ) 8 A.8º B.10º C.12º D.18º 8.下列四个图案是小明家在瓷砖厂选购的四种地砖图案,其中既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是( ) D C B A 9.如图所示,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2).若将△ABC绕着点C顺时针旋转90º,得到△A'B'C',点A,B的对应点A',B'的坐标分别为(a,b),(c,d),则(ab-cd)2017的值为( ) A.0 B.1 C.-1 D.无法计算 10. 如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将 △BCD绕着点B逆时针旋转60º,得到△BAE,连接ED,则下列结论中:①AE∥BC;②∠DEB= 60º;③∠ADE=∠BDC,其中正确结论的序号是( ) A.①② B.①③ C.②③ D.只有① 二、填空题(每小题4分,共24分) 11.在平面直角坐标系中,点M(a+1,2),N(-3,b-1)关于原点对称,则ab=_____. 12.下列图形:①平行四边形;②菱形;③等边三角形;④正方形,其中既是轴对称图形,又是中心对称图形的有_____(填序号). 13.如图所示是小明家一座古老的钟表,该钟表分针的运动可以看做是一种旋转现象,分针匀速旋转时,它的旋转中心是该钟表的旋转轴的轴心,那么该钟表分针经过20分钟旋转了______度. 8 第13题图 A B 第14题图 E D C 第16题图 14.如图所示,Rt△ABC(其中∠ACB=90º)绕着直角顶点C逆时针方向旋转至△DEC,点B恰好落在DE上,若AC=12,CE=5,BE=4,则BD的长为______. 15.在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为_____. 16.如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B= 120º,OA=2,将菱形OABC绕原点顺时针旋转105º至OA'B'C'的位置,则点B'的坐标为_____. 三、解答题(共66分) 17.(6分)如图所示,已知点O是四边形ABCD的边DC的中点,请你作出四边形ABCD关于点O成中心对称的四边形. A O D · B C 第17题图 A B F 第18题图 C E D 第19题图 18.(8分)如图所示,将△ABC绕着点A顺时针旋转30º得到△ADE,DE交AB于点F,若AC=AB,∠BAC=50º,求∠BFD的度数. 19.(8分)已知△ABC在平面直角坐标系中的位置如图所示. ⑴写出A,B,C三点的坐标; ⑵将△ABC绕着点C顺时针方向旋转90º后得到△A1B1C,画出旋转后的△A1B1C,并写出A1,B1的坐标. 20.(10分)如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,在Rt△ABC中,已知直角边BC=5,AC=7,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到如图②所示的“数学风车”. 8 ⑴这个风车是中心对称图形吗?若是,指出这个风车至少需要绕着它的中心旋转多少度才能和它本身重合; ⑵求这个风车的外围周长(即求图②中的实线的长). ② 第20题图 ① 第21题图 21.(10分)如图所示,在平面直角坐标系中,△PQR是由△ABC经过某种变换后得到的图形. ⑴仔细观察点A和点P,点B和点Q,点C和点R的坐标之间的关系,在这种变换下分别写出这六个点的坐标,从中你发现什么特征?请你用文字语言将你发现的特征表达出来; ⑵若△ABC内有一点M(2a+5,-1-3b)经过变换后,在△PRQ内的坐标为(-3,-2),根据你发现的特征,求关于x的方程2-ax=bx-3的解. 22.(12分)阅读下列材料,并完成相应的任务: 几何中,除了我们常见的四边形外,还有些特殊的四边形其形状与我们生活中常见的物体相似,我们可形象地把它们命名,比如筝形,如图①,已知每个网格中小正方形的边长为1,阴影部分形状似箭头状,我们形象地称它为“箭头四边形”. ① ④ ③ ② 第22题图 ⑴图①中,“箭头四边形”的面积为______; ⑵请你以图①为基本图案,在图②所示的的8×8的网格中重新设计一个是轴对称图形,但不是中心对称图形的图案; ⑶请你以图①为基本图案,在图③所示的的8×8的网格中重新设计一个是中心对称图形,但不是轴对称图形的图案; 8 ⑷请你以图①为基本图案,在图④所示的的8×8的网格中重新设计一个既是中心对称图形又是轴对称图形的图案. 23.(12分)在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得到△A′BO′,点A,O旋转后的对应点分别为A′,O′,记旋转角为α. (1)如图①,若α=90°,求AA′的长; (2)如图②,若α=120°,求点O′的坐标. 附加题(20分,不计入总分) 24.综合与探究 两块等腰直角三角尺△ABC和△DEC如图所示摆放,其中∠ACB=∠DCE=90º,F是DE的中点,H是AE的中点,G是BD的中点. ⑴如图①,若点D,E分别在AC,BC的延长线上,通过观察和测量,猜想FH和FG的数量关系和位置关系,并证明你的猜想. ⑵如图②,若将三角尺△DEC绕着点C顺时针旋转至A,C,E在一条直线上时,其余条件均不变,则⑴中的猜想是否还成立,若成立,请加以证明;若不成立,请说明理由. ⑶如图③,将图①中的△DEC绕着点C顺时针旋转一个锐角,得到图③,⑴中的猜想还成立吗?请直接写出结论,不用证明. ① ② ③ 第24题图 8 第二十三章 旋转章末检测题(A)参考答案 一、1.C 2.B 3.D 4.A 5.B 6.C 7.C 8.C 9.C 10.A 二、11. 12.②④ 13.120 14.9 15. (2,1) 16.( 三、17.解:如图所示,连接AO并延长AO到A1,使OA1=AO,连接BO并延长BO到B1,使OB1=BO, 连接CA1,A1,B1,B1D,则四边形A1B1DC就是所求作的四边形. A O D · B C B1 A1 18. 解:∵∠BAC=50º,AC=AB, ∴∠C=∠B=×(180º-50º)=65º. 由旋转的性质可得∠D=∠C=65º,∠CAD=30º. ∴∠DAB=50º-30º=20º. ∴∠BFD=∠D+∠DAB=65º+20º=85º. 19.解:⑴A(-1,2),B(-3,1),C(0,-1), ⑵如图,A1(3,0),B1(2,2) A1 B1 20.解:⑴这个风车是中心对称图形,这个风车至少需要绕着它的中心旋转90度才能和它本身重合; ⑵风车的其中一个直角三角形的较短直角边长为5,较长直角边长为7+5=12,则斜边长为13,所以这个风车的外围周长为4×(5+13)=4×18=72. 21.解:⑴A(4,3),B(3,1),C(1,2),P(-4,-3),Q(-3,-1),R(-1,-2),△ABC所在平面上各点与△PQR所在平面的对应点关于原点对称. 8 ⑵由⑴得解得 ∴2+x=-x-3,解得x=-. 所以关于x的方程2-ax=bx-3的解为x=- 22.解:⑴4 ⑵如图: ⑶如图: ⑷如图: 23.解:(1)∵点A(4,0),点B(0,3), ∴OA=4,OB=3. ∴AB==5. ∵△ABO绕点B逆时针旋转90°,得△A′BO′, ∴BA=BA′,∠ABA′=90°. ∴△ABA′为等腰直角三角形, ∴AA′=BA=5. (2)作O′H⊥y轴于点H. ∵△ABO绕点B逆时针旋转120°,得△A′BO′, ∴BO=BO′=3,∠OBO′=120°. ∴∠HBO′=60°. 在Rt△BHO′中,∵∠BO′H=90°-∠HBO′=30°, ∴BH=BO′=. ∴O′H=. 8 ∴OH=OB+BH=3+=. ∴点O′的坐标为(,). 24.解:⑴猜想FH=FG,FH⊥FG. 证明:∵△ACB和△DCE都是等腰直角三角形,且∠ACB=∠DCE=90º,CD=CE,AC=BC, ∴A,C,D和B,C,E都在一条直线上,AD=BE. ∵F,H分别是DE,AE的中点, ∴FH∥AD,FH=AD, 同理FG∥EB,FG=EB. ∴FH=FG. ∵AD⊥BE, ∴FH⊥FG. ⑵成立. 证明:∵CE=CD,∠ECD=∠ACD=90º,AC=BC, ∴△ACD≌△BCE. ∴AD=BE,∠ADC=∠BEC. 由⑴知,FH=AD,FH∥AD,FG=BE,FG∥BE, ∴FH=FG. 延长AD交BE于点I. ∵∠ADC+∠CAD=90º, ∴∠BEC=∠CAD=90º. ∴∠AIE=90º ∴FH⊥FG. ∴⑴中的猜想成立. ⑶⑴中的猜想成立,结论是FH=FG,FH⊥FG. 8查看更多