- 2021-06-18 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西省吉安市吉水县第二中学2020届高三上学期11月月考数学(理)试卷
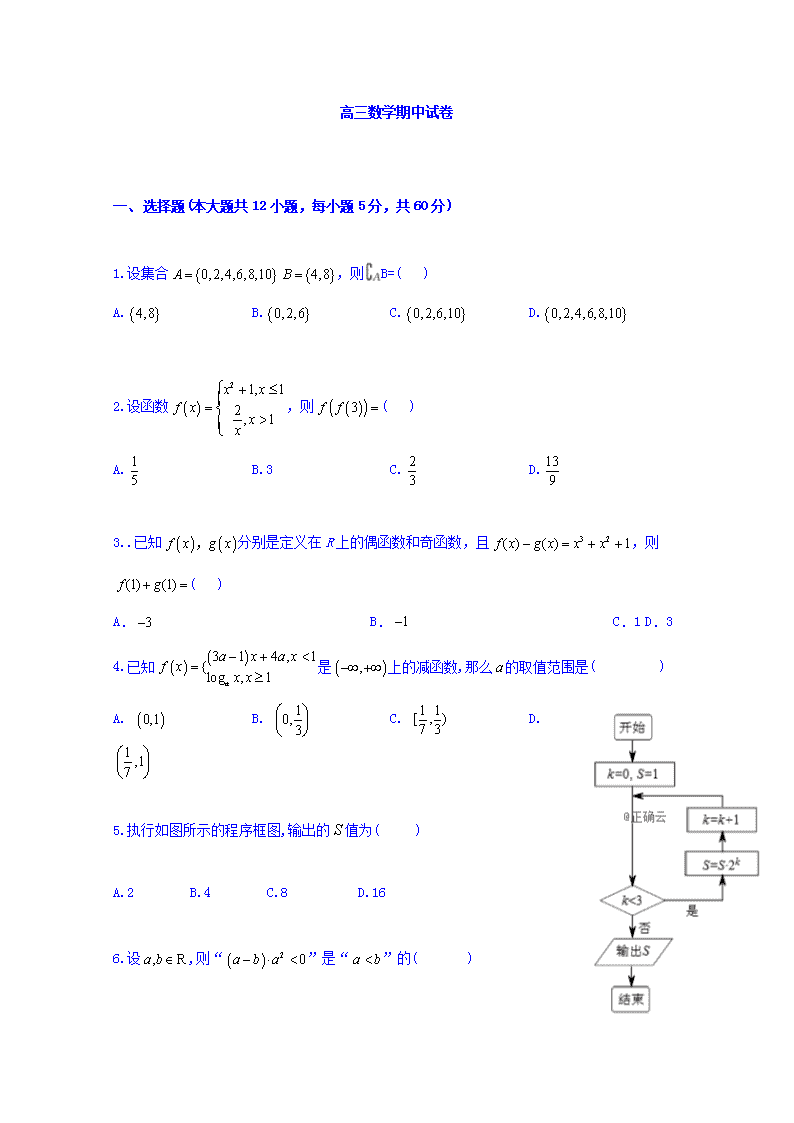
高三数学期中试卷 一、 选择题(本大题共12小题,每小题5分,共60分) 1.设集合,则B=( ) A. B. C. D. 2.设函数,则( ) A. B.3 C. D. 3..已知分别是定义在R上的偶函数和奇函数,且,则( ) A. B. C.1 D.3 4.已知是上的减函数,那么的取值范围是( ) A. B. C. D. 5.执行如图所示的程序框图,输出的值为( ) A.2 B.4 C.8 D.16 6.设,则“”是“”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 7.甲、乙、丙三名同学选修课程,在4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( ) A.36种 B.48种 C.96种 D.192种 8.为了得到函数的图象,只需把函数的图象上所有的点( ) A.向左平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向右平移个单位长度 9.已知向量,若,则与的夹角为() A. B. C. D. 10.已知函数的导函数为,且满足,则( ) A. B.-1 C.1 D.e 11.设、、则的大小关系为( ) A. B. C. D. 12.设变量满足约束条件,则目标函数的最大值为( ) A.12 B.10 C.8 D.2 二、填空题 13.若函数为奇函数,则实数__________ 14.已知是虚数单位,若,则的值为__________. 15定积分 . 16.已知两个正数满足,则使不等式恒成立的实数m的范围是__________ 三、解答题 17.(10分)已知集合,. (1)若,求实数m的取值范围; (2)当时,求A的非空真子集的个数; 18.(12分)设锐角三角形的内角的对边分别为已知. (1)求B的大小; (1)若,,求b的值. 19. (12分)某商场举行购物抽奖活动,抽奖箱中放有编号分别为1,2,3,4,5的五个小球.小球除编号不同外,其余均相同.活动规则如下:从抽奖箱中随机抽取一球,若抽到的小球编号为3,则获得奖金100元;若抽到的小球编号为偶数,则获得奖金50元;若抽到其余编号的小球,则不中奖.现某顾客依次有放回的抽奖两次. 1.求该顾客两次抽奖后都没有中奖的概率; 2.求该顾客两次抽奖后获得奖金之和为100元的概率. 20. (12分)设数列的前项和为,已知. 1.求数列的通项公式; 2.若数列满足,求数列的前项和. 21. (12分)设函数,曲线在点处的切线方程为. (1)求 的解析式; (2)证明:曲线上任意一点处的切线与直线和直线所围成的三角形的面积为定值,并求此定值. 22. (12分)已知函数. (1)若,求的单调区间; (2)是否存在实数a,使的最小值为0?若存在,求出a的值;若不存在,说明理由. 参考答案 一、选择题 1.答案:C 解析:由补集定义知B=,故选C. 2.答案:D 解析:由题意得,从而. 3.答案:C 解析:∵,∴.又为偶函数,为奇函数,∴,∴. 4.答案:C 解析: ∵是减函数, ∴ 且. ∵为减函数, ∴,∴ 又∵是上的减函数, ∴,∴ ∴ 5.答案:C 解析:; 循环 ; 循环; 停止,输出,所以答案为C. 6.答案:A 解析:若,则,且,所以充分性成立;若,则,当时, ,所以必要性不成立.故“”是“”的充分而不必要条件. 7.答案:C 解析:甲选修门,有种选法,乙、丙各选修门,各有种选法,由分步乘法计数原理得,共有种选法. 8.答案:D 解析:因为,所以只需把函数的图象上所有的点向右平移个单位长度即可.故选D. 9.答案:C 解析:依题意,得. 设与的夹角为,而, 所以.又, 所以. 所以与的夹角为. 10.答案:B 解析:,令,得,解得,故选B. 11.答案:D 解析:∵,,,∴ 12.答案:B 解析:画出可域如图中阴影部分所示,目标函数可转化为, 作出直线并平移,显然当其过点时纵截距最大.解方程组得,∴. 二、填空题 13.答案: 解析: 因为函数是奇函数,所以 即,解得 答案: 14.答案:2 解析:因为.又,所以且,得,所以. 答案: 解析: 本题考查有关多项式函数,三角函数定积分的应用. . 16.答案: 解析:由题意知两个正数满足, 则, 当时取等号;∴的最小值是 , ∵不等式恒成立,∴. 故答案为: . 三、解答题 17.答案:(1)因为,所以,当时,,则; 当时,根据题意作出如图所示的数轴,可得,解得. 综上可得,实数m的取值范围是. (2)当时,,共有8个元素,所以A的非空真子集的个数为. (3) 当时,由(1)题知;当时,根据题意作出如图所示的数轴, 可得,或,解得. 综上可得,实数m的取值范围是. 解析: 18.答案:(1)根据正弦定理,得: , ∵,∴. ∴为锐角三角形,∴. (2)根据余弦定理,得: , ∴. 解析: 19.答案:1.由题意得,该顾客有放回的抽奖两次的所有可能结果为: , , , , 共有25种情况. 设“该顾客两次抽奖后都没有中奖”为事件A,则事件A包含的结果为,共4种, 所以. 即该顾客两次抽奖后都没有中奖的概率为. 2.两次抽奖奖金之和为100元包括三种情况: ①第一次奖金为100元,第二次没有获奖,其包含的情况为,概率为; ②第一次没中奖,第二次奖金为100元,其包含的情况为,概率为; ③两次各获奖金50元,包含的情况有,概率为. 由互斥事件有一个发生的概率公式可得所求概率为, 即该顾客两次抽奖后获得奖金之和为元的概率为. 解析: 20.答案:1.由,得, . 而,则 2.由及. 可得, ① ② ①-②得 . . 解析: 21.答案:(1). ∵点在切线上, ∴. 又曲线在点处的切线方程为, ∴, ∴. (2)设为曲线上任意一点, 则曲线在该点处的切线的斜率, 切线方程为, 令,得. 由,得, ∴曲线上任意一点处的切线与直线和直线所围成的三角形的面积,为定值. 解析: 22.答案:(1)∵且, ∴. 可得函数. ∵真数为, ∴函数定义域为. 令 可得: 当时,t为关于x的增函数; 当时,t为关于x的减函数. ∵底数为 ∴函数的单调增区间为,单调减区间为. (2)设存在实数a,使的最小值为0,由于底数为, 可得真数恒成立,且真数t的最小值恰好是1, 即a为正数,且当时,t值为1. 所以, 所以,使的最小值为0. 解析:查看更多