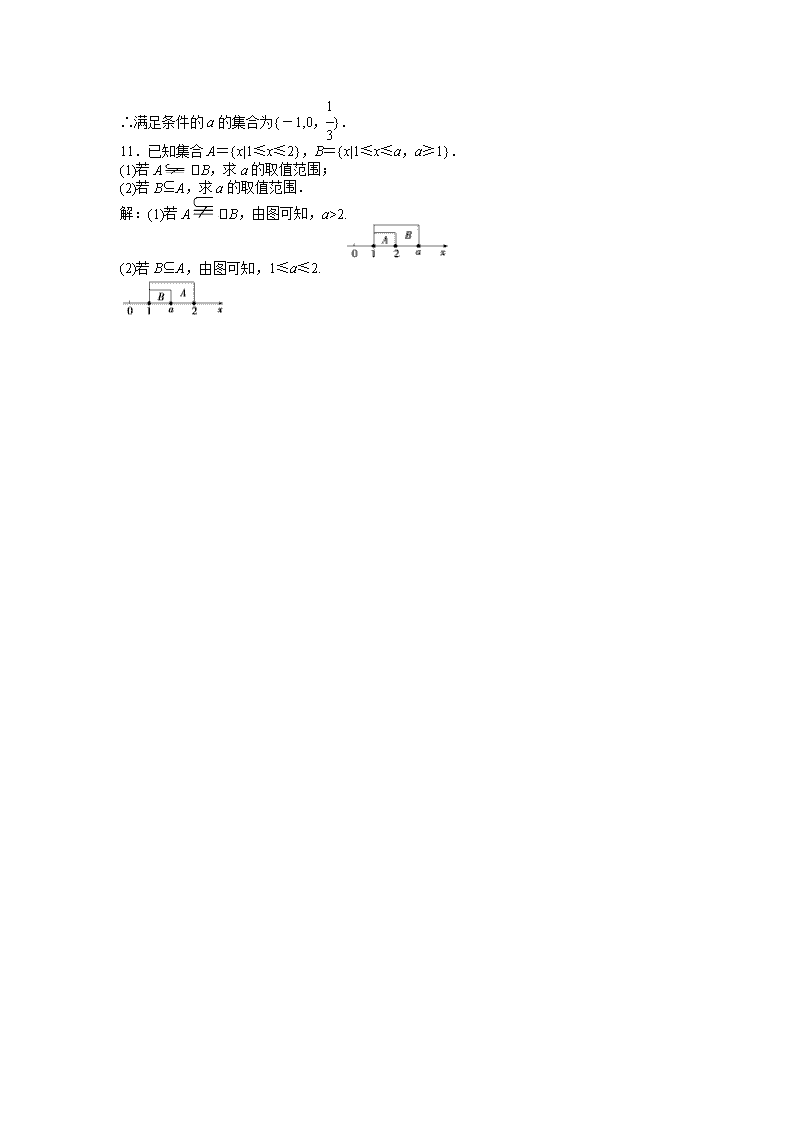高中数学必修1人教A同步练习试题及解析第1章1_1_2同步训练及详解
高中数学必修一同步训练及解析
1.下列集合中是空集的是( )
A.{x|x2+3=3}
B.{(x,y)|y=-x2,x,y∈R}
C.{x|-x2≥0}
D.{x|x2-x+1=0,x∈R}
解析:选D.∵方程x2-x+1=0的判别式Δ<0,∴方程无实根,故D选项为空集,A选项中只有一个元素0,B选项中有无数个元素,即抛物线y=-x2上的点,C选项中只有一个元素0.
2.已知集合A={x|-1
B
B.AB
C.BA
D.A⊆B
解析:选C.利用数轴(图略)可看出x∈B⇒x∈A,但x∈A⇒x∈B不成立.
3.下列关系中正确的是________.
①∅∈{0};②∅{0};③{0,1}⊆{(0,1)};④{(a,b)}={(b,a)}.
解析:∅{0},∴①错误;空集是任何非空集合的真子集,②正确;{(0,1)}是含有一个元素的点集,③错误;{(a,b)}与{(b,a)}是两个不等的点集,④错误,故正确的是②.
答案:②
4.图中反映的是四边形、梯形、平行四边形、菱形、正方形这五种几何图形之间的关系,则A、B、C、D、E分别代表的图形的集合为__________________________.
解析:
由以上概念之间的包含关系可知:集合A={四边形},集合B={梯形},集合C={平行四边形},集合D={菱形},集合E={正方形}.
答案:A={四边形},B={梯形},C={平行四边形},D={菱形},E={正方形}
[A级 基础达标]
1.如果A={x|x>-1},那么( )
A.0⊆A
B.{0}∈A
C.∅∈A
D.{0}⊆A
解析:选D.A、B、C的关系符号是错误的.
2.若{1,2}={x|x2+bx+c=0},则( )
A.b=-3,c=2
B.b=3,c=-2
C.b=-2,c=3
D.b=2,c=-3
解析:选A.由题意知1,2为方程x2+bx+c=0的两个根,所以解得b=-3,c=2.
3.符合条件{a}P⊆{a,b,c}的集合P的个数是( )
A.2
B.3
C.4
D.5
解析:选B.集合P中一定含有元素a,且不能只有a一个元素,用列举法列出即可.
4.设x,y∈R,A={(x,y)|y=x},B={(x,y)|=1},则A、B间的关系为________.
解析:(0,0)∈A,而(0,0)∉B,故BA.
答案:BA
5.已知集合A={-1,3,2m-1},集合B={3,m2}.若B⊆A,则实数m=________.
解析:由于B⊆A,则应有m2=2m-1,于是m=1.
答案:1
6.已知集合A={(x,y)|x+y=2,x,y∈N},试写出A的所有子集.
解:∵A={(x,y)|x+y=2,x,y∈N},
∴A={(0,2),(1,1),(2,0)}.
∴A的子集有:∅,{(0,2)},{(1,1)},{(2,0)},{(0,2),(1,1)},{(0,2),(2,0)},{(1,1),(2,0)},{(0,2),(1,1),(2,0)}.
[B级 能力提升]
7.集合M={x|x2+2x-a=0,x∈R},且∅M,则实数a的取值范围是( )
A.a≤-1
B.a≤1
C.a≥-1
D.a≥1
解析:选C.∅M等价于方程x2+2x-a=0有实根.即Δ=4+4a≥0.解得a≥-1.
8.设A={x|12.
(2)若B⊆A,由图可知,1≤a≤2.