2019高考数学（理）冲刺大题提分（讲义+练习）大题精做6 立体几何：平行、垂直关系证明（理）

2019高考数学（理）冲刺大题提分（讲义+练习）大题精做6 立体几何：平行、垂直关系证明（理）

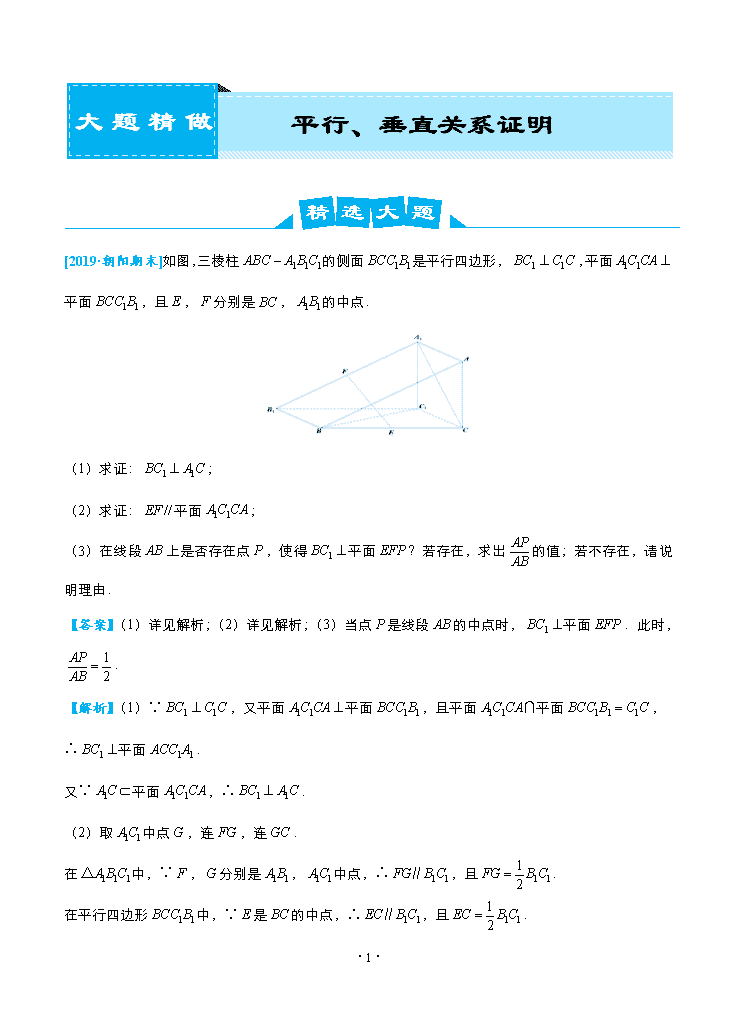
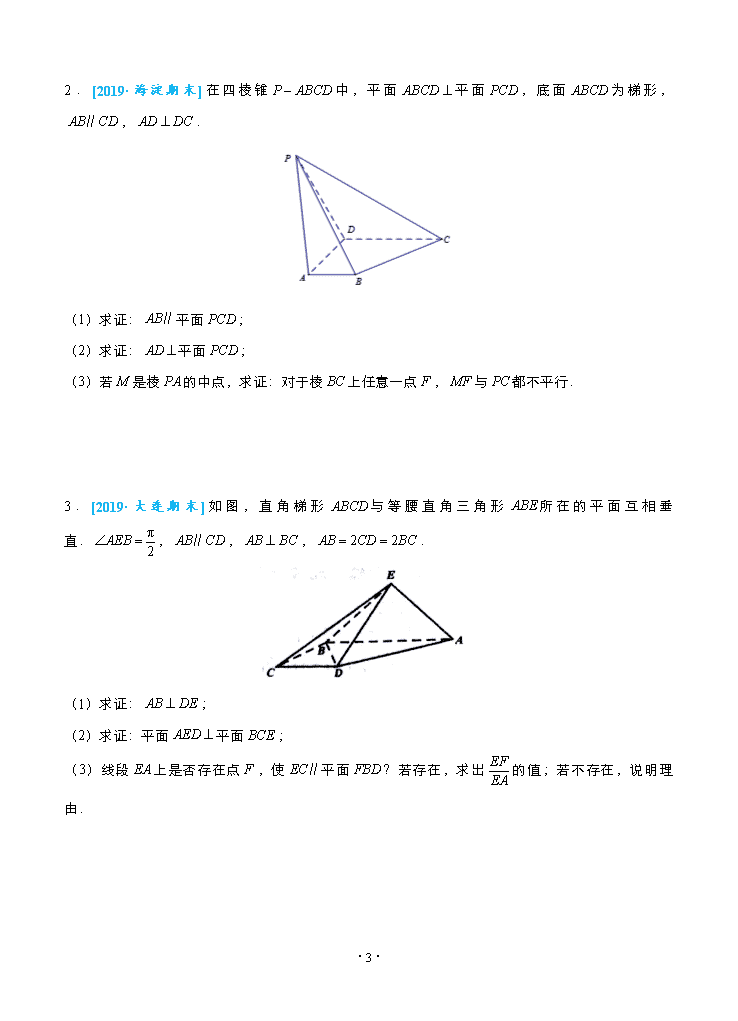
平行、垂直关系证明 大题精做六 精选大题 ‎[2019·朝阳期末]如图，三棱柱的侧面是平行四边形，，平面平面，且，分别是，的中点．‎ ‎（1）求证：；‎ ‎（2）求证：平面；‎ ‎（3）在线段上是否存在点，使得平面？若存在，求出的值；若不存在，请说明理由．‎ ‎【答案】（1）详见解析；（2）详见解析；（3）当点是线段的中点时，平面．此时，．‎ ‎【解析】（1）∵，又平面平面，且平面平面，‎ ‎∴平面．‎ 又∵平面，∴．‎ ‎（2）取中点，连，连．‎ 在中，∵，分别是，中点，∴，且．‎ 在平行四边形中，∵是的中点，∴，且．‎ ‎·6·‎ ‎∴，且．∴四边形是平行四边形．∴．‎ 又∵平面，平面，∴平面．‎ ‎（3）在线段上存在点，使得平面．‎ 取的中点，连，连．‎ ‎∵平面，平面，平面，∴，．‎ 在中，∵，分别是，中点，∴．‎ 又由（2）知，∴，．‎ 由得平面．‎ 故当点是线段的中点时，平面．此时，．‎ 模拟精做 ‎1．[2019·无锡期末]在四棱锥中，锐角三角形所在平面垂直于平面，，．‎ ‎（1）求证：平面；‎ ‎（2）求证：平面平面．‎ ‎·6·‎ ‎2．[2019·海淀期末]在四棱锥中，平面平面，底面为梯形，，．‎ ‎（1）求证：平面；‎ ‎（2）求证：平面；‎ ‎（3）若是棱的中点，求证：对于棱上任意一点，与都不平行．‎ ‎3．[2019·大连期末]如图，直角梯形与等腰直角三角形所在的平面互相垂直．，，，．‎ ‎（1）求证：；‎ ‎（2）求证：平面平面；‎ ‎（3）线段上是否存在点，使平面？若存在，求出的值；若不存在，说明理由．‎ ‎·6·‎ 答案与解析 ‎1．【答案】（1）见解析；（2）见解析．‎ ‎【解析】（1）四边形中，∵，，‎ ‎∴，在平面外，∴平面．‎ ‎（2）作于，‎ ‎∵平面平面，而平面平面，‎ ‎∴平面，∴，‎ 又，，∴平面，‎ 又在平面内，∴平面平面．‎ ‎2．【答案】（1）见证明；（2）见证明；（3）见证明．‎ ‎【解析】（1）∵，平面，平面，∴平面．‎ ‎（2）法一：∵平面平面，平面平面，‎ ‎，平面，∴平面．‎ 法二：在平面中过点作，交于，‎ ‎∵平面平面，平面平面，平面，‎ ‎∴平面，‎ ‎∵平面，∴，‎ 又，，∴平面．‎ ‎（3）法一：假设存在棱上点，使得，‎ ‎·6·‎ 连接，取其中点，‎ 在中，∵，分别为，的中点，∴，‎ ‎∵过直线外一点只有一条直线和已知直线平行，∴与重合，‎ ‎∴点在线段上，∴是，的交点，‎ 即就是，而与相交，矛盾，‎ ‎∴假设错误，问题得证．‎ 法二：假设存在棱上点，使得，显然与点不同 ，‎ ‎∴，，，四点在同一个平面中，‎ ‎∴，，∴，，‎ ‎∴就是点，，确定的平面，且，‎ 这与为四棱锥矛盾，∴假设错误，问题得证．‎ ‎3．【答案】（1）详见解析；（2）详见解析；（3）存在点，且时，有平面．‎ ‎【解析】（1）证明：取中点，连结，．由等腰直角三角形可得，‎ ‎∵，，∴，‎ ‎∵四边形为直角梯形，，，‎ ‎∴四边形为正方形，∴，，平面，‎ ‎∴．‎ ‎（2）∵平面平面，平面平面，且，‎ ‎∴平面，∴，‎ 又∵，，∴平面，平面，‎ ‎·6·‎ ‎∴平面平面．‎ ‎（3）解：存在点，且时，有平面，连交于，‎ ‎∵四边形为直角梯形，，∴，‎ 又，∴，∴，‎ ‎∵平面，平面，‎ ‎∴平面．即存在点，且时，有平面．‎ ‎·6·‎