- 2021-06-07 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学中二次函数压轴题分类总结超无重复附答案
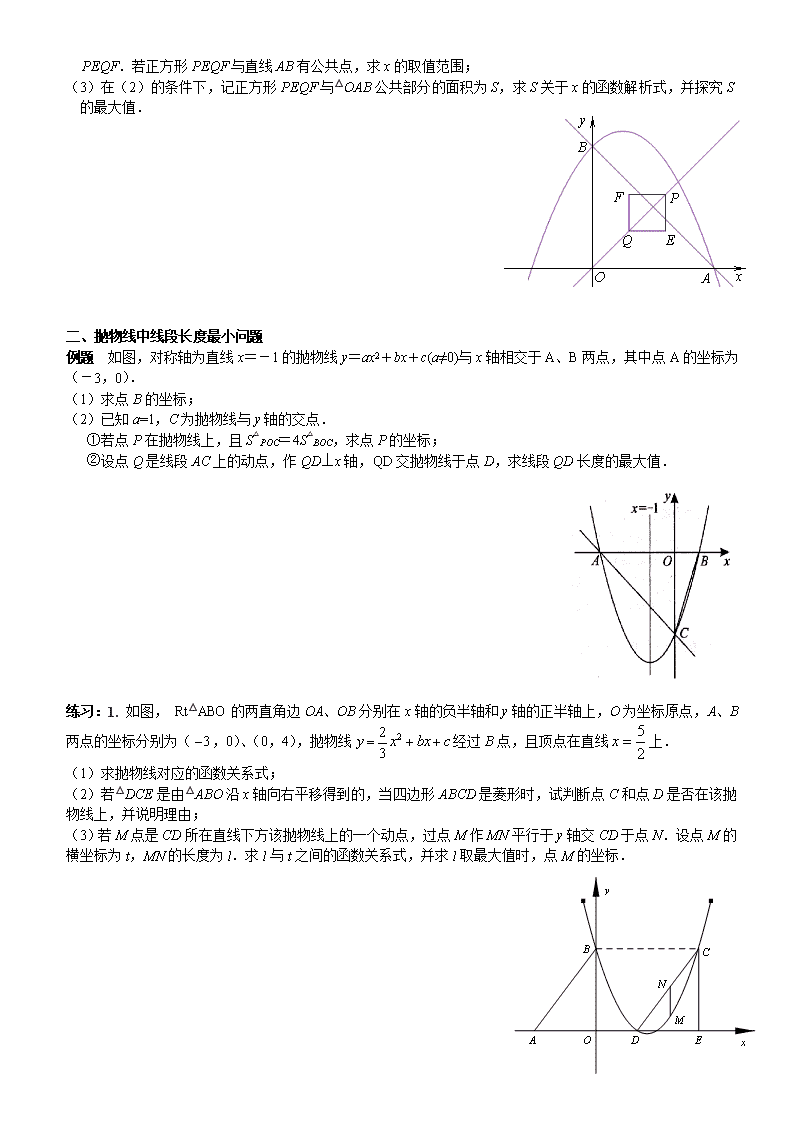
中考数学专题训练 二次函数压轴题 一、抛物线关于三角形面积问题 例题 二次函数的图象,其顶点坐标为M(1,). (1)求出图象与轴的交点A,B的坐标; (2)在二次函数的图象上是否存在点P,使,若存在,求出P点的坐标;若不存在,请说明理由; (3)将二次函数的图象在轴下方的部分沿轴翻折,图象的其余部分不变,得到一个新的图象,请你结合这个新的图象回答:当直线与此图象有两个公共点时,的取值范围. 练习:1. 如图.平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,线段AB交y轴与点E. (1)求点E的坐标;(2)求抛物线的函数解析式; (3)点F为线段OB上的一个动点(不与O、B重合),直线EF 与抛物线交与M、N两点(点N在y轴右侧),连结ON、BN,当点F在线段OB上运动时,求BON的面积的最大值,并求出此时点N的坐标; 2. 如图,已知抛物线交x轴的正半轴于点A,交y轴于点B. (1)求A、B两点的坐标,并求直线AB的解析式; (2)设()是直线上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形 PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围; (3)在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值. 二、抛物线中线段长度最小问题 例题 如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-3,0). (1)求点B的坐标; (2)已知a=1,C为抛物线与y轴的交点. ①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标; ②设点Q是线段AC上的动点,作QD⊥x轴,QD交抛物线于点D,求线段QD长度的最大值. [中国#@*教~育出&版网] 练习:1. 如图, Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(,0)、(0,4),抛物线经过B点,且顶点在直线上. (1)求抛物线对应的函数关系式; (2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由; (3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标. 三、抛物线与线段和最小的问题 例题 如图,已知抛物线与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.(1)若抛物线过点M(﹣2,﹣2),求实数a的值; (2)在(1)的条件下,解答下列问题; ①求出△BCE的面积; ②在抛物线的对称轴上找一点H,使CH+EH的值最小,直接写出点H的坐标. 练习:1. 如图,已知二次函数的图象与坐标轴交于点A(-1, 0)和点B(0,-5). (1)求该二次函数的解析式; (2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标. x O A B y (3)在(2)的条件下,在x轴上找一点M,使得△APM是等腰三角形,请直接写出所有符合条件的点M的坐标. 2. 如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G. (1)求抛物线的函数解析式,并写出顶点D的坐标; (2)在直线EF上求一点H,使△CDH的周长最小,并求出H的坐标; C E D G A x y O B F (3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积. 四、抛物线与等腰三角形 例题:已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴. (1)求抛物线的函数关系式; (2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标; (3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由. 练习:1. .如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线 (1)求抛物线的解析式; (2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标. 2. 如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根. (1)求抛物线的解析式; (2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD. ①当△OPC为等腰三角形时,求点P的坐标; ②求△BOD 面积的最大值,并写出此时点D的坐标. 3. 如图,已知抛物线于x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3). (1)求抛物线的解析式; (2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形,若存在,求出符合条件的点P的坐标;若不存在,请说明理由:[ (3)若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标。 五、抛物线与直角三角形 例题 如图,抛物线经过点A(﹣3,0),B(1.0),C(0,﹣3). (1)求抛物线的解析式; (2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标; (3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由. 练习:1. 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:的顶点. (1)求A、B两点的坐标; (2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由; (3)当△BDM为直角三角形时,求m的值. 2. 如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D. (1)求b,c的值; (2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标; (3)在(2)的条件下: ①求以点E、B、F、D为顶点的四边形的面积; ②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由. 六、抛物线与四边形 y x O A B C 例题 1. 如图,抛物线经过A(-1,0),B(5,0),C(0,-)三点. (1)求抛物线的解析式; (2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标; (3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. 练习:1. 如图,在平面直角坐标系中,直线与轴交于点A,与y轴交于点C. 抛物线经过A、C两点,且与x轴交于另一点B(点B在点A右侧). (1)求抛物线的解析式及点B坐标; (2)若点M是线段BC上一动点,过点M的直线EF平行y轴交轴于点F,交抛物线于点E.求ME长的最大值; (3)试探究当ME取最大值时,在抛物线x轴下方是否存在点P,使以M、F、B、P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由. 2. 如图,已知二次函数图像的顶点坐标为(2,0),直线与二次函数的图像交于A、B两点,其中点A在y轴上. (1)二次函数的解析式为y= ; (2)证明点不在(1)中所求的二次函数的图像上; (3)若C为线段AB的中点,过C点作轴于E点,CE与二次函数的图像交于D点. ① y轴上存在点K,使以K、A、D、C为顶点的四边形是平行四边形,则K点的坐标是 ; ②二次函数的图像上是否存在点P,使得?若存在,求出P点坐标;若不存在,请说明理由. 例1. 解:(1)A,B两点的坐标分别为A(-1,0),B(3,0) (2)故P点坐标为(-2,5)或(4,5) (3)b的取值范围为 练1. (2)∴y=1/4x2-1/2x, (3)依题意,得直线OB的解析式为y=x,设过N点且与直线OB平行的直线解析式为y=x+m,与抛物线解析式联立,得出关于x的一元二次方程,当△=0时,△BON面积最大,N(3,3/4);此时△BON面积=27/4 练2. 解:(1)所以直线AB的解析式为; (2); (3)①当时, ,,, ②当时, ,,,综合①②得,当时,。 例二 :(1)点A(-3,0),点B(1,0) (2)点P的坐标(4,21)、(-4,5) (3)x=-3/2,QD最大值9/4. 二练1. (1) (2) (3) 例三.(1)a=4; (2) (3) 三练1、(1) (2)要使△ABP的周长最小,只要PA+PB最小;因而BC与对称轴x=2的交点P就是所求的点;点P(2,-3) 三练2、(1) (2)由于CD是定长,若△CDH的周长最小,那么CH+DH的值最小,由于EF垂直平分线段BC,那么B、C关于直线EF对称,所以BD与EF的交点即为所求的H点; 例四:(1)(2) (3) 练四1、(1)y=-1/2x^2-1/2x+3;(2)M坐标(0,0)或(3√2-3,0) 2、(1) (2) (3) 3、 五.(1) (2) 练五1、(1) (2) 练五2、(1) (2) (3) 例六 、(1) (2) (3) 练六1、(1)抛物线的解析式为y=x^2-2x-3,点B坐标为(3,0); (2)直线BC y=x-3,设M(x,x-3)E(x,x^2-2x-3),ME=x-3-(x^2-2x-3)=(x-3/2)^2+9/4,ME的最大值为9/4; (3)当ME取最大值时,M的坐标为(3/2,-3/2),F的坐标为(3/2,0),FB=3/2,抛物线的对称x=1,所以点M不在对称上,故在抛物线x轴下方不存在点P,使以M,F,B,P为顶点的四边形是平行四边形。 练六2、(1)(2) (3)查看更多