2011年高考数学人教版北京卷

2011年高考数学人教版北京卷

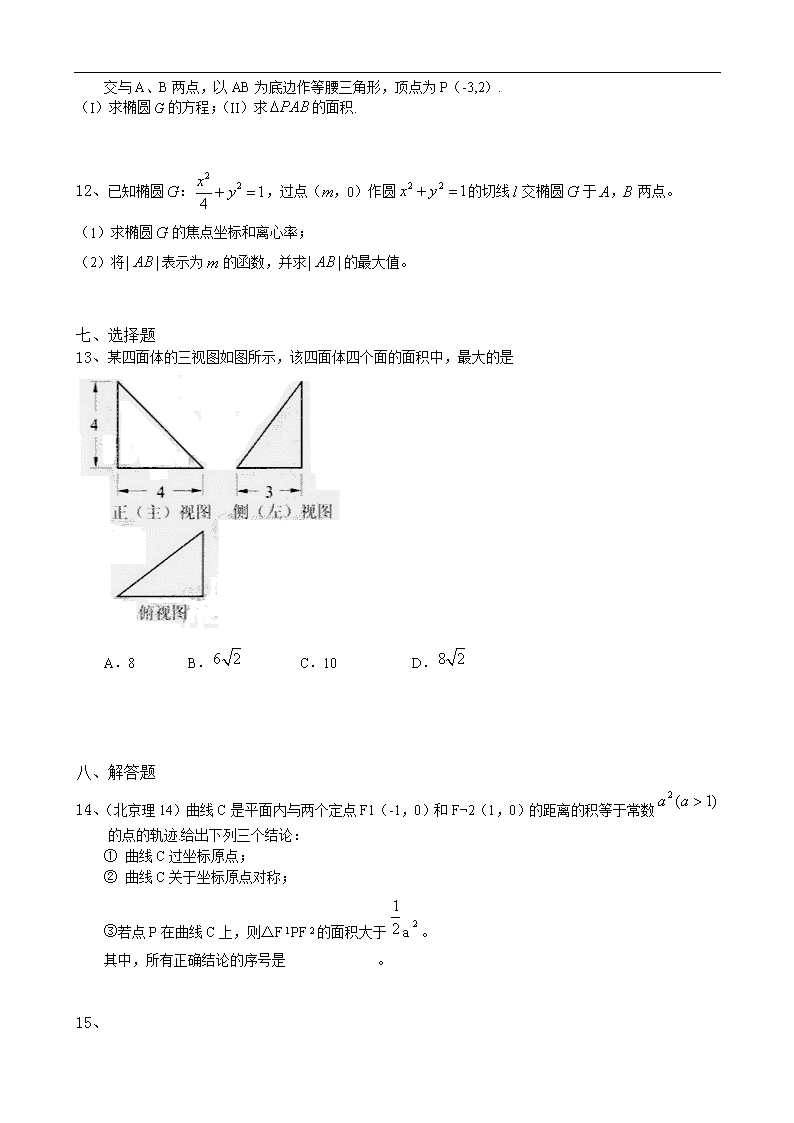
‎2011年数学人教版北京卷 一、选择题 ‎1、（北京理6）根据统计，一名工人组装第x件某产品所用的时间（单位：分钟）为（A，c为常数）。已知工人组装第4件产品用时30分钟，组装第A件 ‎ 产品时用时15分钟，那么c和A的值分别是 A. 75，25 B. 75，‎16 C. 60，25 D. 60，16‎ ‎2、（北京文8）已知点,,若点在函数的图象上，则使得的面积为2的点的个数为 ‎ A. 4 B. ‎‎3 C. 2 D. 1‎ ‎3、已知集合P=｛x︱x2≤1｝,M=｛a｝.若P∪M=P,则a的取值范围是 ‎ A．(-∞, -1] B．[1, +∞） ‎ ‎ C．[-1，1] D．（-∞，-1] ∪[1，+∞）‎ 二、填空题 ‎4、（北京理13）已知函数，若关于x的方程有两个不同的实根，则实数k的取值范围是________.‎ 三、解答题 ‎5、（北京理18）已知函数.‎ ‎(1)求的单调区间；‎ ‎(2)若对，，都有，求的取值范围。‎ ‎6、已知函数，（I）求的单调区间；‎ ‎（II）求在区间上的最小值。‎ 四、选择题 ‎7、在极坐标系中，圆的圆心的极坐标是 A. B. C. D. ‎ ‎8、已知点A（0,2），B（2,0）．若点C在函数y = x的图像上，则使得ΔABC的面积为2的点C的个数为 ‎ ‎ A．4 B．‎3 ‎ C．2 D．1‎ ‎9、设A（0，0），B（4，0），C（，4），D（t，4）（），记N（t）为平行四边形ABCD内部（不含边界）的整点的个数，其中整数点是指横、纵坐标都是整数的点，则函数N（t）的值域为 ‎ A．{ 9，10，11 } B．{ 9，10，12 }‎ C．{ 9，11，12 } D．{ 10，11，12 }‎ 五、填空题 ‎10、曲线C是平面内与两个定点和的距离的积等于常数的点的轨迹，给出下列三个结论：‎ ‎①曲线C过坐标原点；‎ ‎②曲线C关于坐标原点对称；‎ ‎③若点P在曲线C上，则的面积不大于.‎ 其中，所有正确结论的序号是____________.‎ 六、解答题 ‎11、（本小题共14分）‎ 已知椭圆的离心率为，右焦点为（,0），斜率为I的直线与椭圆G 交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3,2）.‎ ‎（I）求椭圆G的方程；（II）求的面积.‎ ‎12、已知椭圆G：，过点（m，0）作圆的切线l交椭圆G于A，B两点。‎ ‎（1）求椭圆G的焦点坐标和离心率；‎ ‎（2）将表示为m的函数，并求的最大值。‎ 七、选择题 ‎13、某四面体的三视图如图所示，该四面体四个面的面积中，最大的是 ‎ A．8 B． C．10 D．‎ 八、解答题 ‎14、（北京理14）曲线C是平面内与两个定点F1（-1，0）和F¬2（1，0）的距离的积等于常数的点的轨迹.给出下列三个结论：‎ ‎ ① 曲线C过坐标原点；‎ ‎ ② 曲线C关于坐标原点对称；‎ ‎ ③若点P在曲线C上，则△FPF的面积大于a。‎ 其中，所有正确结论的序号是 。‎ ‎15、‎ ‎（北京理19） ‎ ‎ 已知椭圆.过点（m,0）作圆的切线I交椭圆G于A，B两点.‎ ‎ （I）求椭圆G的焦点坐标和离心率；‎ ‎ （II）将表示为m的函数，并求的最大值.‎ ‎（19）（共14分）‎ ‎16、（北京理16） ‎ ‎ 如图，在四棱锥中，平面，底面是菱形，.‎ ‎(Ⅰ)求证：平面 ‎ （Ⅱ）若求与所成角的余弦值；‎ ‎ （Ⅲ）当平面与平面垂直时，求的长.‎ ‎ ‎ 九、选择题 ‎17、执行如图所示的程序框图，输出的s的值为A. ；B. ；C. ； D. ‎ ‎18、（北京理4）执行如图所示的程序框图，输出的s值为 ‎ A．-3‎ ‎ B．-‎ ‎ C．‎ ‎ D．2‎ 十、解答题 ‎19、北京文16．（本小题共13分）‎ ‎ 以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊，无法确认，在图中以X表示.‎ ‎ （1）如果X=8，求乙组同学植树棵树的平均数和方差；‎ ‎（2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.‎ ‎ ‎ ‎ （注：方差其中为的平均数）‎ 十一、选择题 ‎20、某车间分批生产某种产品，每批的生产准备费用为800元.若每批生产x件，则平均仓储时间为天，且每件产品每天的仓储费用为1元.为使平均没见产品的生产准备费用与仓储费用之和最小，每批应生产产品 ‎ A．60件 B. 80件 C．100件 D．120件 十二、填空题 ‎21、北京理用数字2，3组成四位数，且数字2，3至少都出现一次，这样的四位数共有______个(用数字作答)‎ 十三、解答题 ‎22、以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊，无法确认，在图中以X表示。‎ ‎（1）如果，求乙组同学植树棵数的平均数和方差；‎ ‎（2）如果，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数Y的分布列和数学期望。‎ ‎（注：方差，其中为，，…，的平均数）‎ ‎23、（北京理17）以下茎叶图记录了甲、乙两组个四名同学的植树棵树。乙组记录中有一个数据模糊，无法确认，在图中以X表示。‎ ‎ （Ⅰ）如果X=8,求乙组同学植树棵树的平均数和方差；‎ ‎ （Ⅱ）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵树 Y的分布列和数学期望。‎ ‎ （注：方差，其中为，，…… 的平均数）‎ ‎24、（本小题共13分）‎ ‎ 以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊，无法确认，在图中以X表示.‎ ‎ （1）如果X=8，求乙组同学植树棵树的平均数和方差；‎ ‎（2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.‎ ‎ （注：方差其中为的平均数）‎ ‎25、以下茎叶图记录了甲、乙两组个四名同学的植树棵树。乙组记录中有一个数据模糊，无法确认，在图中以X表示。‎ ‎ （Ⅰ）如果X=8,求乙组同学植树棵树的平均数和方差；‎ ‎ （Ⅱ）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵树Y的分布列和数学期望。‎ ‎ （注：方差，其中为，，…… 的平均数）‎ 十四、填空题 ‎26、（北京理9）在中。若b=5，，tanA=2，则sinA=____________；a=_______________。‎ 十五、解答题 ‎27、已知函数。‎ ‎ （Ⅰ）求的最小正周期：‎ ‎ （Ⅱ）求在区间上的最大值和最小值。‎ ‎28、（北京理20）‎ ‎ 若数列满足，数列为数列，记=．‎ ‎ （Ⅰ）写出一个满足，且〉0的数列；‎ ‎ （Ⅱ）若，n=2000，证明：E数列是递增数列的充要条件是=2011；‎ ‎ （Ⅲ）对任意给定的整数n（n≥2），是否存在首项为0的E数列，使得=0？如果存在，写出一个满足条件的E数列；如果不存在，说明理由。‎ ‎ ‎ ‎29、已知函数.‎ ‎(1)求的单调区间；‎ ‎(2)若对，，都有，求的取值范围。‎ ‎30、已知函数，（I）求的单调区间；‎ ‎（II）求在区间上的最小值。‎ 以下是答案 一、选择题 ‎1、D ‎【解析】由条件可知，时所用时间为常数，所以组装第4件产品用时必然满足第一个分段函数，即，，选D。‎ ‎2、A ‎3、C 二、填空题 ‎4、‎ ‎【解析】单调递减且值域为(0,1]，单调递增且值域为，有两个不同的实根，则实数k的取值范围是（0,1）。‎ 三、解答题 ‎5、解：(1)，令得 当时，在和上递增，在上递减；‎ 当时，在和上递减，在上递增 ‎(2) 当时，；所以不可能对，都有；‎ 当时有（1）知在上的最大值为，所以对，都有 即，故对，都有时，的取值范围为。‎ ‎6、解：（I），令；所以在上递减，在上递增；‎ ‎（II）当时，函数在区间上递增，所以；‎ 当即时，由（I）知，函数在区间上递减，上递增，所以；‎ 当时，函数在区间上递减，所以。‎ 四、选择题 ‎7、【解析】：，圆心直角坐标为（0,-1），极坐标为，选B。‎ ‎8、A ‎9、C 五、填空题 ‎10、②③‎ 六、解答题 ‎11、解：（Ⅰ）由已知得解得，又 所以椭圆G的方程为 ‎（Ⅱ）设直线l的方程为 由得 设A、B的坐标分别为AB中点为E，‎ 则；因为AB是等腰△PAB的底边，‎ 所以PE⊥AB.所以PE的斜率解得m=2。‎ 此时方程①为解得所以 所以|AB|=.此时，点P（—3，2）到直线AB：的距离 所以△PAB的面积S=‎ ‎12、解：（Ⅰ）由已知得所以 所以椭圆G的焦点坐标为，离心率为 ‎（Ⅱ）由题意知，.当时，切线l的方程，‎ 点A、B的坐标分别为此时 当m=－1时，同理可得 当时，设切线l的方程为 由；设A、B两点的坐标分别为，则；‎ 又由l与圆 所以 由于当时，因为 且当时，|AB|=2，所以|AB|的最大值为2.‎ 七、选择题 ‎13、C 八、解答题 ‎14、②③‎ ‎15、解：（Ⅰ）由已知得 所以 所以椭圆G的焦点坐标为 离心率为 ‎（Ⅱ）由题意知，.‎ 当时，切线l的方程，点A、B的坐标分别为 此时 当m=－1时，同理可得 当时，设切线l的方程为 由 设A、B两点的坐标分别为，则 又由l与圆 所以 由于当时，‎ 所以.‎ 因为 且当时，|AB|=2，所以|AB|的最大值为2.‎ ‎16、证明：（Ⅰ）因为四边形ABCD是菱形，‎ 所以AC⊥BD.‎ 又因为PA⊥平面ABCD.‎ 所以PA⊥BD.‎ 所以BD⊥平面PAC.‎ ‎（Ⅱ）设AC∩BD=O.‎ 因为∠BAD=60°，PA=PB=2,‎ 所以BO=1，AO=CO=.‎ 如图，以O为坐标原点，建立空间直角坐标系O—xyz，则 P（0，—，2），A（0，—，0），B（1，0，0），C（0，，0）.‎ 所以 设PB与AC所成角为，则 ‎.‎ ‎（Ⅲ）由（Ⅱ）知 设P（0，－，t）（t>0），‎ 则 设平面PBC的法向量,‎ 则 所以 令则 所以 同理，平面PDC的法向量 因为平面PCB⊥平面PDC,‎ 所以=0，即 解得 所以PA=‎ 九、选择题 ‎17、【解析】：循环操作4次时S的值分别为，选D。‎ ‎18、D 十、解答题 ‎19、（共13分）‎ 解（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，‎ 所以平均数为 方差为 ‎（Ⅱ）记甲组四名同学为A1，A2，A3，A4，他们植树的棵数依次为9，9，11，11；乙组四名同学为B1，B2，B3，B4，他们植树的棵数依次为9，8，9，10，分别从甲、乙两组中随机选取一名同学，所有可能的结果有16个，它们是：‎ ‎ （A1，B1），（A1，B2），（A1，B3），（A1，B4），‎ ‎ （A2，B1），（A2，B2），（A2，B3），（A2，B4），‎ ‎ （A3，B1），（A2，B2），（A3，B3），（A1，B4），‎ ‎ （A4，B1），（A4，B2），（A4，B3），（A4，B4），‎ ‎ 用C表示：“选出的两名同学的植树总棵数为‎19”‎这一事件，则C中的结果有4个，它们是：（A1，B4），（A2，B4），（A3，B2），（A4，B2），故所求概率为 十一、选择题 ‎20、B 十二、填空题 ‎21、【解析】个数为。‎ 十三、解答题 ‎22、（共13分）‎ 解（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，‎ 所以平均数为 方差为 ‎（Ⅱ）当X=9时，由茎叶图可知，甲组同学的植树棵树是：9，9，11，11；乙组同学的植树棵数是：9，8，9，10。分别从甲、乙两组中随机选取一名同学，共有4×4=16种可能的结果，这两名同学植树总棵数Y的可能取值为17，18，19，20，21事件“Y=17”等价于“甲组选出的同学植树9棵，乙组选出的同学植树8棵”所以该事件有2种可能的结果，因此P（Y=17）=‎ 同理可得 所以随机变量Y的分布列为：‎ Y ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ P EY=17×P（Y=17）+18×P（Y=18）+19×P（Y=19）+20×P（Y=20）+21×P（Y=21）=17×+18×+19×+20×+21×‎ ‎=19‎ ‎23、解：（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，‎ 所以平均数为 方差为 ‎（Ⅱ）当X=9时，由茎叶图可知，甲组同学的植树棵树是：9，9，11，11；乙组同学的植树棵数是：9，8，9，10。分别从甲、乙两组中随机选取一名同学，共有4×4=16种可能的结果，这两名同学植树总棵数Y的可能取值为17，18，19，20，21事件“Y=17”等价于“甲组选出的同学植树9棵，乙组选出的同学植树8棵”所以该事件有2种可能的结果，因此P（Y=17）=‎ 同理可得 所以随机变量Y的分布列为：‎ Y ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ P EY=17×P（Y=17）+18×P（Y=18）+19×P（Y=19）+20×P（Y=20）+21×P（Y=21）=17×+18×+19×+20×+21×‎ ‎=19‎ ‎24、（共13分）‎ 解（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，‎ 所以平均数为 方差为 ‎（Ⅱ）记甲组四名同学为A1，A2，A3，A4，他们植树的棵数依次为9，9，11，11；乙组四名同学为B1，B2，B3，B4，他们植树的棵数依次为9，8，9，10，分别从甲、乙两组中随机选取一名同学，所有可能的结果有16个，它们是：‎ ‎ （A1，B1），（A1，B2），（A1，B3），（A1，B4），‎ ‎ （A2，B1），（A2，B2），（A2，B3），（A2，B4），‎ ‎ （A3，B1），（A2，B2），（A3，B3），（A1，B4），‎ ‎ （A4，B1），（A4，B2），（A4，B3），（A4，B4），‎ ‎ 用C表示：“选出的两名同学的植树总棵数为‎19”‎这一事件，则C中的结果有4个，它们是：（A1，B4），（A2，B4），（A3，B2），（A4，B2），故所求概率为 ‎25、（共13分）‎ 解（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，‎ 所以平均数为 方差为 ‎（Ⅱ）当X=9时，由茎叶图可知，甲组同学的植树棵树是：9，9，11，11；乙组同学的植树棵数是：9，8，9，10。分别从甲、乙两组中随机选取一名同学，共有4×4=16种可能的结果，这两名同学植树总棵数Y的可能取值为17，18，19，20，21事件“Y=17”等价于“甲组选出的同学植树9棵，乙组选出的同学植树8棵”所以该事件有2种可能的结果，因此P（Y=17）=‎ 同理可得 所以随机变量Y的分布列为：‎ Y ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ P EY=17×P（Y=17）+18×P（Y=18）+19×P（Y=19）+20×P（Y=20）+21×P（Y=21）=17×+18×+19×+20×+21×‎ ‎=19‎ 十四、填空题 ‎26、‎ 十五、解答题 ‎27、解：（Ⅰ）因为 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 所以的最小正周期为 ‎ （Ⅱ）因为 ‎ 于是，当时，取得最大值2；‎ ‎ 当取得最小值—1.‎ ‎28、解：（Ⅰ）0，1，2，1，0是一具满足条件的E数列A5。‎ ‎（答案不唯一，0，1，0，1，0也是一个满足条件的E的数列A5）‎ ‎（Ⅱ）必要性：因为E数列A5是递增数列，‎ 所以.‎ 所以A5是首项为12，公差为1的等差数列.‎ 所以a2000=12+（2000—1）×1=2011.‎ 充分性，由于a2000—a1000≤1，‎ a2000—a1000≤1‎ ‎……‎ a2—a1≤1‎ ‎ 所以a2000—a≤19999，即a2000≤a1+1999.‎ ‎ 又因为a1=12，a2000=2011,‎ ‎ 所以a2000=a1+1999.‎ ‎ 故是递增数列.‎ ‎ 综上，结论得证。‎ ‎ （Ⅲ）令 ‎ 因为 ‎ ……‎ ‎ ‎ 所以 因为 所以为偶数,‎ 所以要使为偶数,‎ 即4整除.‎ 当 时，有 当的项满足，‎ 当不能被4整除，此时不存在E数列An，‎ 使得 ‎29、解：(1)，令得 当时，在和上递增，在上递减；‎ 当时，在和上递减，在上递增 ‎(2) 当时，；所以不可能对，都有；‎ 当时有（1）知在上的最大值为，所以对，都有即，故对，都有时，的取值范围为。‎ ‎30、解：（I），令；所以在上递减，在上递增；‎ ‎（II）当时，函数在区间上递增，所以；‎ 当即时，由（I）知，函数在区间上递减，上递增，所以；‎ 当时，函数在区间上递减，所以。‎