- 2021-06-03 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版七年级数学(下册)第二章测试卷(附参考答案)
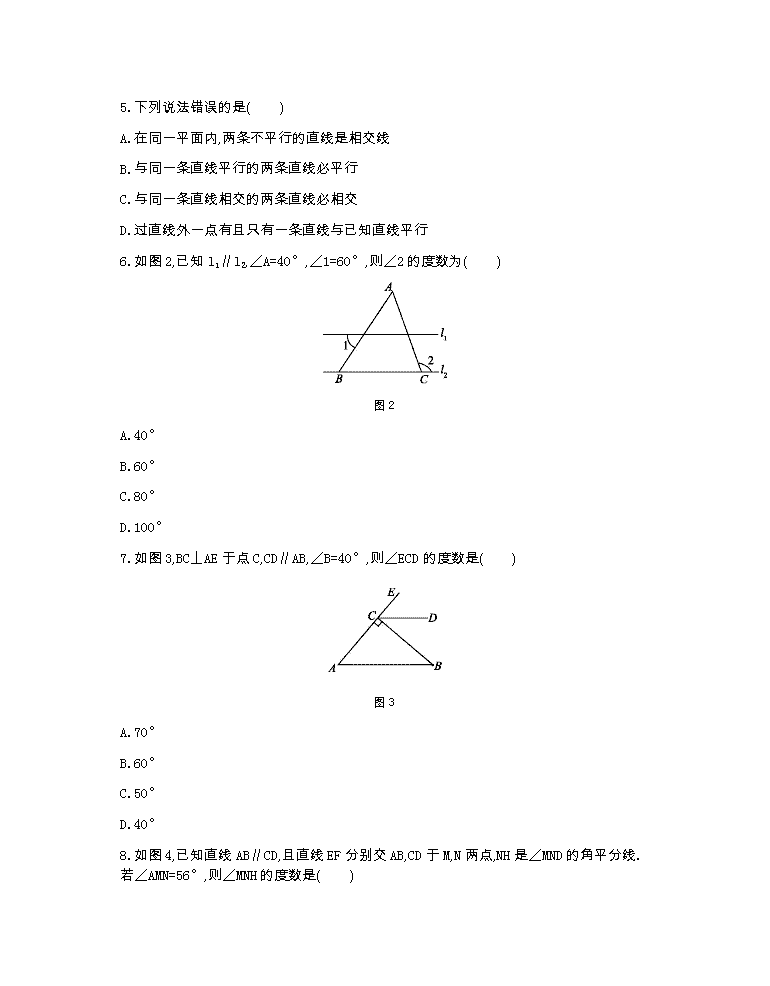
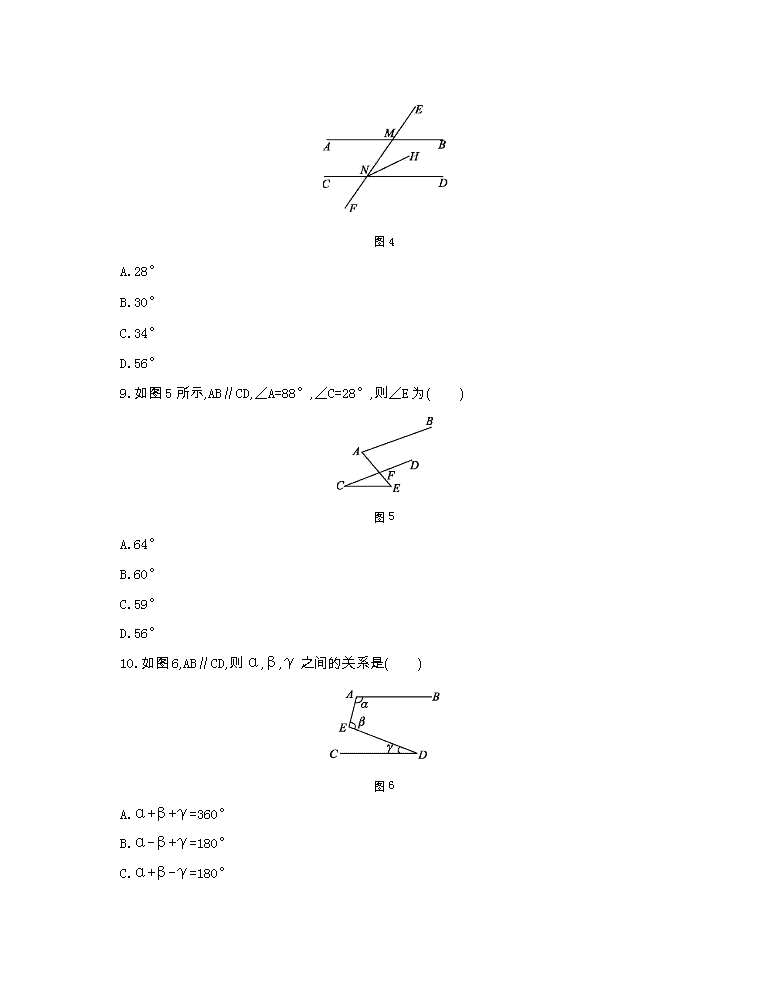
数学七下北师测试卷第二章 1.图1中共有对顶角( ) 图1 A.5对 B.6对 C.7对 D.8对 2.下列说法中:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确的个数是( ) A.2 B.3 C.4 D.5 3.下列作图语句正确的是( ) A.以点O为圆心作弧 B.延长射线AB到点C C.作∠AOB,使∠AOB=∠1 D.作直线AB,使AB=a 4.如果一个角的补角是150°,那么这个角的余角的度数是( ) A.30° B.60° C.90° D.120° 5.下列说法错误的是( ) A.在同一平面内,两条不平行的直线是相交线 B.与同一条直线平行的两条直线必平行 C.与同一条直线相交的两条直线必相交 D.过直线外一点有且只有一条直线与已知直线平行 6.如图2,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为( ) 图2 A.40° B.60° C.80° D.100° 7.如图3,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( ) 图3 A.70° B.60° C.50° D.40° 8.如图4,已知直线AB∥CD,且直线EF分别交AB,CD于M,N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( ) 图4 A.28° B.30° C.34° D.56° 9.如图5所示,AB∥CD,∠A=88°,∠C=28°,则∠E为( ) 图5 A.64° B.60° C.59° D.56° 10.如图6,AB∥CD,则α,β,γ之间的关系是( ) 图6 A.α+β+γ=360° B.α-β+γ=180° C.α+β-γ=180° D.α+β+γ=180° 11.如图7,直线a和直线b相交于点O,∠1=50°,则∠2= . 图7 12.如图8所示,已知∠1=∠2,∠B=40°,则∠3= . 图8 13.如图9,直线l1∥l2,AB⊥CD,∠1=34°,那么∠2= . 图9 14.如图10,AB∥CD,AD⊥AC,∠ADC=32°,则∠CAB的度数是 . 图10 15.如图11所示,添加条件: ,可使AC∥DF;添加条件: ,可使AB∥DE.(每空只填一个条件即可) 图11 16.将两块三角板的直角顶点重合为如图12所示的位置,若∠BOC=80°,则∠AOD= . 图12 17.如图13,AB∥CD,BC∥DE,那么∠B+∠D= . 图13 18.如图14,A,B之间是一座山,一条铁路要通过A,B两点,为此需要在A,B之间挖一条笔直的隧道,在A地测得铁路走向是北偏东63°,那么B地按南偏西 度的方向施工,才能使铁路在山腰准确接通. 图14 19.如图15,∠1=100°,∠2=100°,∠3=120°,求∠4.填空: 图15 因为∠1=∠2=100°(已知), 根据“ ”, 所以m∥n. 根据“ ” ∴∠ =∠ . 又∵∠3=120°(已知), ∴∠4= . 20.如图16,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数. 图16 21.已知:∠α,线段m,如图17所示,按下列步骤作图. (1)作∠AOB=∠α; (2)在射线OA上,顺次截取OC=CD=DE=m; (3)在射线OB上任取一点P,连接EP; (4)分别过C,D两点作EP的平行线,交OB于M,N; (5)比较OM,MN,NP的大小(借助圆规而不用刻度尺测量). 图17 22.如图18,已知AB∥CD. (1)判断∠FAB与∠C的大小关系,并说明理由; (2)若∠C=35°,AB是∠FAD的平分线. 图18 23.如图19,AF平分∠BAC,DE平分∠BDF,且∠1=∠2,试说明DE∥AF,DF∥AC. 图19 24.如图20,∠ADE=∠B,∠1=∠2,GF⊥AB,试说明:CD⊥AB. 解:因为∠ADE=∠B(已知), 图20 参考答案 1.B 2.A 3.C 4.B 5.C 6.D 7.C 8.A 9.B 10.C 11.50° 12.40° 13.56° 14.122° 15.∠ACB=∠DFE∠B=∠E 16.100° 17.180° 18.63 19.内错角相等,两直线平行两直线平行,同位角相等 3 4 120° 20.解:因为∠AOC=120°, 根据“对顶角相等”, 所以∠BOD=120°. 因为∠AOC+∠AOD=180°, 所以∠AOD=180°-120°=60°. 因为OE平分∠AOD, 所以∠AOE=∠AOD=30°. 21.由作图可知:OM=MN=NP. 22.①求∠FAD的度数; ②若∠ADB=110°,求∠BDE的度数. 解:(1)∠FAB与∠C的大小关系是相等, 理由是:因为AB∥CD, 所以∠FAB=∠C. (2)①因为∠FAB=∠C=35°, AB是∠FAD的平分线, 所以∠FAD=2∠FAB=2×35°=70°. ②因为∠ADB=110°,∠FAD=70°, 所以∠ADB+∠FAD=110°+70°=180°, 所以CF∥BD, 所以∠BDE=∠C=35°. 23.解:因为AF平分∠BAC,DE平分∠BDF,∠1=∠2, 所以∠BDF=∠BAC, 所以DF∥AC(同位角相等,两直线平行). 又因为∠2=∠BAF(角平分线定义), 所以∠1=∠BAF(等量代换), 所以DE∥AF(同位角相等,两直线平行). 24.所以DE∥BC(同位角相等,两直线平行), 所以∠1=∠3(两直线平行,内错角相等). 又因为∠1=∠2,所以∠2=∠3(等量代换), 所以GF∥DC(同位角相等,两直线平行). 又因为GF⊥AB,所以CD⊥AB.查看更多