2020年中考专题复习：垂直模型中的相似及变形

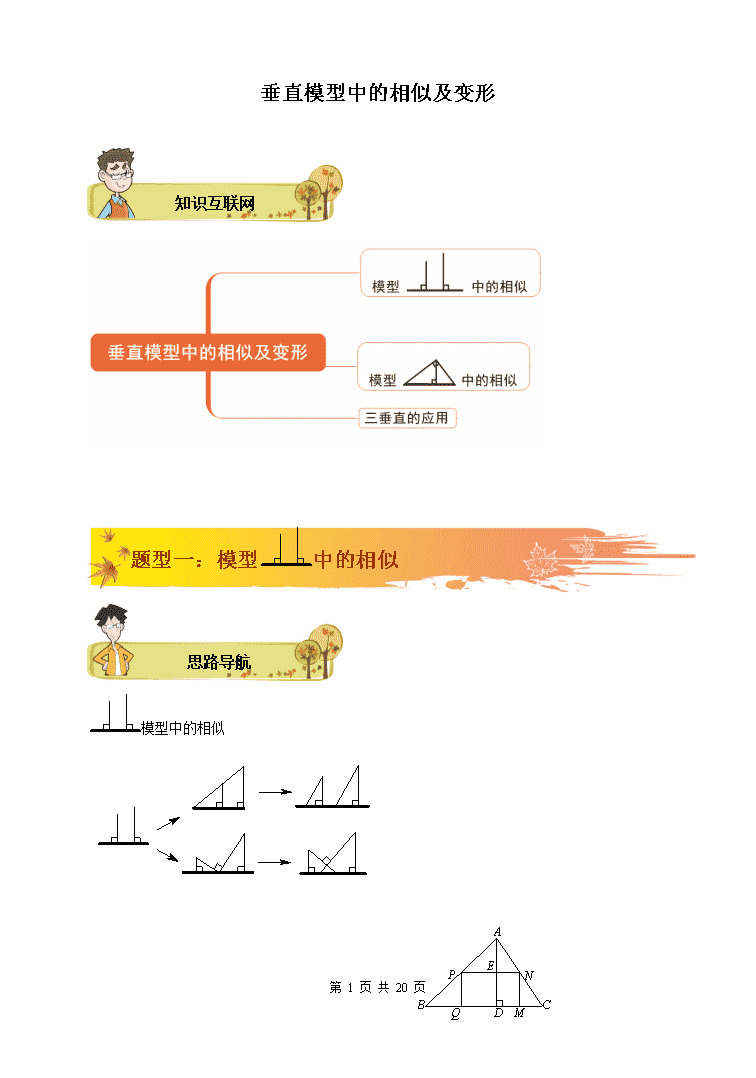
2020年中考专题复习：垂直模型中的相似及变形

垂直模型中的相似及变形 知识互联网 ‎ ‎ 题型一：模型中的相似 思路导航 模型中的相似 ‎[来源:*&^中教%网#]‎ 第 19 页 共 20 页 例题精讲 如图，是一块锐角三角形余料，边mm，高mm，要把它加工成长方形零件，使长方形的边在上，其余两个顶点分别在上．‎ ‎⑴求这个长方形零件面积的最大值；[来源:@#z%zste~*p.com]‎ ‎⑵在这个长方形零件面积最大时，能否将余下的材料剪下再拼成（不计接缝用料及损耗）与长方形大小一样的长方形？若能，试给出一种拼法；若不能，试说明理由．‎ ‎⑴ 设长方形零件的边，则．‎ ‎∵‎ ‎∴，‎ ‎∴，‎ ‎∴[来源%:中~#&教*网]‎ ‎∴ ，解得 ‎ 所以长方形的面积 当时，． ‎ ‎（mm）．‎ 所以这个长方形零件面积的最大值是． ‎ ‎⑵ ∵，‎ ‎∴从理论上说，恰能拼成一个与长方形大小一样的长方形．‎ 第 19 页 共 20 页 拼法：作的中位线，分别过、作的垂线，垂足分别为、，过作的平行线，交、的延长线于、，易知，，所以将剪下拼接到的位置，即得四边形，此四边形即为与长方形零件面积最大时大小一样的长方形．‎ 典题精练 ‎⑴ 如图，在一场羽毛球比赛中，站在场内M处的运动员 林丹把球从N点击到了对方场内的点B，已知网高 OA=1.52米，OB=4米，OM=5米，则林丹起跳后击球点N[中~国教#育出&%版网@]‎ 离地面的距离MN= 米．‎ ‎⑵ 如右图，小华为了测量所住楼房的高度，他请来同学帮 忙，测量了同一时刻他自己的影长和楼房的影长分别是米和米．已知小华的身高为米，那么他所住楼房的高度为 米．‎ ‎⑶ 如图，为估算某河的宽度，在河对岸边选定一个目标点，在近岸取点，，，使得，，点在上，并且点，，在同一条直线上，若测得，，，则河的宽度等于 A． B．‎ C． D．‎ ‎⑷ 如图，正方形中，为的中点，于点，‎ 则等于（　　）‎ A． B． C． D．‎ 第 19 页 共 20 页 ‎⑸ 如图1，用形状相同、大小不等的三块直角三角形木板，恰好能拼成如图2所示的四边形 ‎．若，，那么这个四边形的面积是_____________．‎ ‎⑴ C；⑵ ；⑶ B；⑷ D；⑸ . ‎[来*源:中^教%@网#]‎ 题型二：模型中的相似 思路导航 ‎ ‎ 在中，，于，‎ 则在这个图形中，我们可以得到个直角三角形，‎ 这个直角三角形两两相似，即 进而可以得到组比例关系，这组比例关系中，有个比例式比较特殊：‎ ‎⑴ ；⑵ ；⑶ ，‎ 这个比例式转化为乘积式为：‎ ‎⑴；⑵ ；⑶ ，‎ 这就是著名的“射影定理”‎ 第 19 页 共 20 页 典题精练 ‎[中国教^@育出~&版网%]‎ ‎⑴如图，在中，为直角，于点，，，写出其中的一对相似三角形是________和 _________；并写出它的面积比__________________．‎ ‎⑵ 如图，中，于，一定能确定 为直角三角形的条件的个数是（ ）‎ ‎①； ②； ③；‎ ‎④； ⑤[中国教育&出^*@版网#]‎ A．1　 B．2 C．3 D．4‎ ‎[来#^&源*:@中教网]‎ ‎⑶ 如图，是斜边上的高，如果两条直角边 ‎，则_______．‎ ‎⑴ 答案不唯一，和，；⑵ C； ‎ ‎⑶ ‎ 由题意，，，‎ 则，，‎ 又，，，，，‎ 则，∴．‎ ‎[来~源:*%中国教育出#版网@]‎ 如图，已知中，，是边上中线，是边上的中线，且于点，于点，若，，求的长．‎ 连结[中&@国*教^育出版~网]‎ 第 19 页 共 20 页 ‎∵，‎ ‎∴，即，‎ 又∵，且 则，，‎ ‎∴，，‎ ‎∵是边中线，是边中线，‎ ‎∴，‎ ‎∴，∴，‎ 在中，，‎ ‎∴，∴．‎ 题型三：三垂直的应用 思路导航 三垂直模型中包括三垂直全等和三垂直相似，在解题的过程中要善于发现和使用，并要学会根据具体情况构造三垂直模型.‎ 例题精讲 如图，在矩形中，点、分别在边、上，‎ 第 19 页 共 20 页 ‎，，，，求的长． ‎ ‎∵‎ ‎∴，∴，∴；‎ 在中，‎ 典题精练 ‎[中%@#国教^育*出版网]‎ ‎⑴如图，梯形中，，，为上一点，且，若，，，则= ．‎ ‎⑵如图，已知，，是线段的中点，且，，，那么 ． ‎ ‎⑴ 10；⑵ 4‎ ‎[来源:zz~step.^c%&#om]‎ ‎[来&源~^:@中教网*]‎ ‎⑴ 如图，正方形ABCD的边长为10，内部有6个全等的正方形，小正方形的顶点E.F、G、H分别落在边AD.AB.BC.CD上，则DE的长为 ．‎ ‎⑵ 如图，一个边长分别为、、的直角三角形的一个顶点与正方形的顶点重合，另两个顶点分别在正方形的两条边、‎ 第 19 页 共 20 页 上，那么这个正方形的面积是 ． [ww@w.#zzstep~.^com*]‎ ‎⑴ 2．‎ ‎⑵ ．‎ 抓住相似模型．‎ ‎，[中~国&^教育出%版网@]‎ ‎∴‎ 设，，∴‎ 在中，‎ ‎，∴‎ 正方形的面积为．‎ ‎⑴ 等边△ABC边长为6，P为BC边上一点，∠MPN=60°，且PM、PN分别于边AB.AC交于点E.F. 如图，若点P在BC边上运动，且∠MPN绕点P旋转，当CF=AE=2时，求PE的长. [来源:@#z%zstep~*.com]‎ ‎⑵ 如图，梯形中，∥，，‎ ‎，点 分别在线段上，且 ‎，若，求长．‎ ‎[来源^:中~#&教*网]‎ ‎【解析】⑴ 可证△EBP∽△PCF.‎ ‎∴ ．‎ 第 19 页 共 20 页 设BP=x，则 ．解得 .‎ ‎∴ PE的长为4或．‎ ‎⑵ 在梯形中，∥， ，，‎ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴△∽△‎ ‎∴[中~国教#育出&%版网@]‎ 即： 解得：．‎ 如图，在矩形中，为中点，交于，连结．‎ ‎⑴与是否相似？若相似，证明你的结论；若不相似，请说明理由．‎ ‎⑵设，是否存在这样的值，使得与相似， 若存在，证明你的结论，并求出的值；若不存在，说明理由．‎ ‎⑴ 相似．在矩形中，．因为，‎ 第 19 页 共 20 页 ‎、、共线，所以．‎ 又∵，[中*@^国%教育出~版网]‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴‎ 又∵‎ ‎∴‎ ‎⑵ 存在，由于，‎ ‎∴只能是，‎ ‎．‎ 由⑴知，‎ ‎∴．[www.z&^zs#tep.c*o~m]‎ ‎∴．‎ 即．‎ 反过来，在时，，，，‎ ‎，‎ ‎∴．‎ ‎∴．‎ 第 19 页 共 20 页 精讲: 相似三角形经典模型总结 ‎【探究一】模型介绍：‎ ‎⑴ A字型与反A字型；‎ ‎⑵ 8字型与反8字型；‎ ‎[中^国教育%出版&#网*]‎ ‎⑶ 双垂直模型与母子型；‎ ‎[来源:中教^~%网#@]‎ ‎⑷ 三垂直模型与一线三等角模型；‎ ‎⑸ 手拉手相似模型；‎ 第 19 页 共 20 页 ‎【探究二】模型联系： ‎ 思维拓展训练(选讲)‎ 如图，中，，于，平分 第 19 页 共 20 页 交于，于．求证：．‎ 由，，‎ ‎∴‎ ‎∴，即 又∵和中，，‎ ‎∴‎ ‎∴，∴‎ ‎∵是的平分线，，‎ ‎∴，则 已知：如图，在正方形中，，点是边上的动点（点不与端点重合），的垂直平分线分别交于点，交的延长线于点．‎ ‎⑴ 设，试用含的代数式表示的值；[来@源:#*中教^网~]‎ ‎⑵ 在⑴的条件下，当时，求的长．[中国教%育出版@#~&网]‎ ‎⑴ 过点作，分别交于两点．‎ ‎∵是线段的垂直平分线，∴．‎ ‎∵，∴‎ ‎∵H是AE的中点，∴M是AD的中点[中%@#国教^育*出版网]‎ ‎∴是的中位线，∴．‎ ‎∵四边形是正方形，∴四边形是矩形．[来源:#*中教^~网%]‎ ‎∴．‎ ‎∴．‎ 第 19 页 共 20 页 ‎∵，‎ ‎∴．‎ ‎∴，即．　‎ ‎⑵ 过点作于点，则四边形和四边形都是矩形．‎ ‎∵，解得．‎ ‎∴‎ ‎，．‎ ‎∵，‎ ‎∴，即．[来源:*中国教育~出版网@^%]‎ 又∵‎ ‎∴‎ 解得．‎ ‎∴．　‎ 已知，，，，为线段上的动点，点在射线上，且满足（如图1所示）．‎ ‎⑴ 当，且点与点重合时（如图2所示），求线段的长；‎ ‎⑵ 在图1中，连结．当，且点在线段上时，设点之间的距离为，，其中表示的面积，表示的面积，求关于的函数解析式，并写出自变量的范围； [中国&教育#*~出版^网]‎ ‎⑶ 当，且点在线段的延长线上时（如图3所示），求的大小． ‎ 第 19 页 共 20 页 ‎[来@源%:中*^~教网]‎ ‎⑴ 中，，‎ ‎∴，‎ ‎∴，即，‎ 过点作于E，如图⑴则 而 ‎⑵ 如图⑵，过点分别作于，于点.[中^国教*~育@%出版网]‎ ‎∵，[www#.~z%zst@ep^.com]‎ ‎∴‎ ‎∴‎ 设，则，‎ ‎∴‎ ‎，，∴‎ 第 19 页 共 20 页 ‎⑶ 答：‎ 证明：如图⑶，过点分别作于，于点.‎ ‎∵，‎ ‎∴[中国教育*出&%^@版网]‎ ‎∴‎ 又∵，‎ ‎∴‎ ‎∴[来~#源%*:^中国教育出版网]‎ ‎∴‎ ‎∴‎ 等腰直角中，、分别为直角边、上的点，且，过、分别作的垂线，交斜边于、．求证：．‎ 如图，延长至，使，连接 则，于是可证[来源:zzstep%.@~co&*m]‎ 于是 ‎∵‎ 第 19 页 共 20 页 ‎∴‎ ‎∴‎ ‎∴‎ ‎∴[www.%@z&zst*e#p.com]‎ ‎∴．‎ 复习巩固 题型一 模型中的相似 巩固练习 如图，是一块锐角三角形余料，边长毫米，高毫米，要把它加工成正方形零件，使正方形的一边在上，其余两个顶点分别在、上，这个正方形零件的边长是多少？‎ ‎∵四边形为正方形 ‎∴[来^#源:%中教&@网]‎ ‎∴‎ 设边长为，，即 ‎∴（毫米）[中国教&^~育出#*版网]‎ 答：边长为毫米．‎ 题型二 模型中的相似 巩固练习 如图，斜边上的高为，若，，则 ， ， ．‎ 第 19 页 共 20 页 ‎，，．‎ 如图，中，，于，是上任意一点，连结，过作于，求证：．‎ ‎∵，[来源#^:中国%教育出~*版网]‎ ‎∴‎ 又[来%源*:中^&教网#]‎ ‎∴‎ ‎∴，即 又∵为直角三角形，‎ ‎∴‎ 又[中国教育出版~*#%@网]‎ ‎∴‎ ‎∴，即 ‎∴．‎ 如图，在中，，，．点在斜边上，分别作，，垂足分别为、，得四边形．设，．‎ ‎⑴ 用含的代数式表示为 ；‎ ‎⑵ 求与之间的函数关系式，并求出的取值范围；[来#源:中教%&*网~]‎ ‎⑶ 设四边形的面积为，求与之间的函数关系式，并求出的最大值．‎ 第 19 页 共 20 页 ‎⑴ ；[www.z^#z~@ste%p.com]‎ ‎⑵ 可证 ‎∴‎ ‎∴‎ ‎∴‎ ‎⑶ ‎ 当时，取到最大值为．‎ 题型三 三垂直的应用 巩固练习 如图，矩形中，，，将矩形绕点顺时针旋转得到矩形．点为线段上一点（不包括端点），且，求的面积．‎ ‎ ‎ 如图，设，则．‎ ‎∵，∴．‎ 又，‎ ‎∴．‎ 又∵．[中国教#育出版@~^网*]‎ ‎∴‎ ‎∴．即． ‎ 第 19 页 共 20 页 解得，（不符合题意，舍去）．[w*ww.z@%z~step.c^om]‎ ‎∴，即． ‎ 当时，，‎ ‎∴，，‎ ‎． ‎ ‎ ‎ 第 19 页 共 20 页