- 2021-06-02 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010年中考数学压轴题(一)及解答
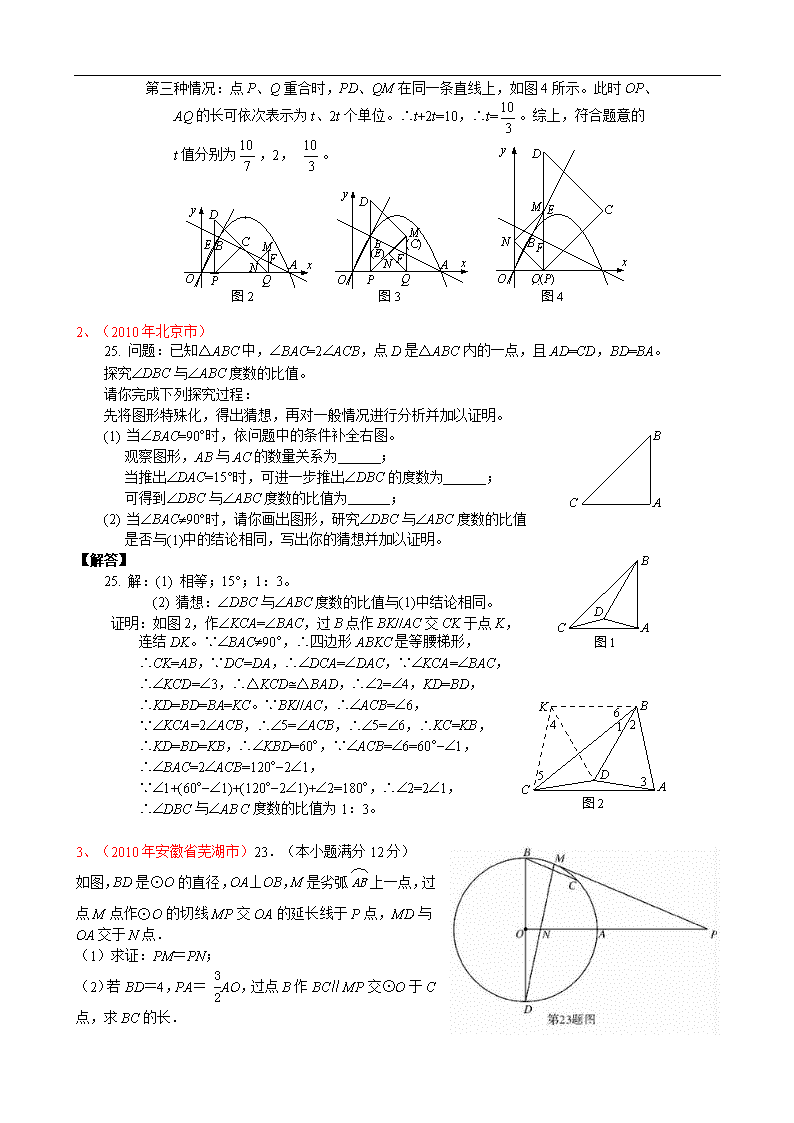
2010年中考数学压轴题(一)及解答 1、(2010年北京市)24. 在平面直角坐标系xOy中,抛物线y= -x2+x+m2-3m+2 x y O 1 1 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上。 (1) 求点B的坐标; (2) 点P在线段OA上,从O点出发向点运动,过P点作x轴的 垂线,与直线OB交于点E。延长PE到点D。使得ED=PE。 以PD为斜边在PD右侧作等腰直角三角形PCD(当P点运动 时,C点、D点也随之运动) j 当等腰直角三角形PCD的顶点C落在此抛物线上时,求 OP的长; k 若P点从O点出发向A点作匀速运动,速度为每秒1个单位,同时线段OA上另一 点Q从A点出发向O点作匀速运动,速度为每秒2个单位(当Q点到达O点时停止 运动,P点也同时停止运动)。过Q点作x轴的垂线,与直线AB交于点F。延长QF 到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当Q 点运动时,M点,N点也随之运动)。若P点运动到t秒时,两个等腰直角三角形分 别有一条直角边恰好落在同一条直线上,求此刻t的值。 【解答】 24. 解:(1) ∵拋物线y= -x2+x+m2-3m+2经过原点,∴m2-3m+2=0,解得m1=1,m2=2, 由题意知m¹1,∴m=2,∴拋物线的解析式为y= -x2+x,∵点B(2,n)在拋物线 y= -x2+x上,∴n=4,∴B点的坐标为(2,4)。 O A B C D E P y x 图1 (2) j 设直线OB的解析式为y=k1x,求得直线OB的解析式为 y=2x,∵A点是拋物线与x轴的一个交点,可求得A点的 坐标为(10,0),设P点的坐标为(a,0),则E点的坐标为 (a,2a),根据题意作等腰直角三角形PCD,如图1。可求 得点C的坐标为(3a,2a),由C点在拋物线上,得 2a= -´(3a)2+´3a,即a2-a=0,解得a1=,a2=0 (舍去),∴OP=。 k 依题意作等腰直角三角形QMN,设直线AB的解析式为y=k2x+b,由点A(10,0), 点B(2,4),求得直线AB的解析式为y= -x+5,当P点运动到t秒时,两个等腰 直角三角形分别有一条边恰好落在同一条直线上,有以下三种情况: 第一种情况:CD与NQ在同一条直线上。如图2所示。可证△DPQ为等腰直角三 角形。此时OP、DP、AQ的长可依次表示为t、4t、2t个单位。∴PQ=DP=4t, ∴t+4t+2t=10,∴t=。 第二种情况:PC与MN在同一条直线上。如图3所示。可证△PQM为等腰直角三 角形。此时OP、AQ的长可依次表示为t、2t个单位。∴OQ=10-2t,∵F点在 直线AB上,∴FQ=t,∴MQ=2t,∴PQ=MQ=CQ=2t,∴t+2t+2t=10,∴t=2。 第三种情况:点P、Q重合时,PD、QM在同一条直线上,如图4所示。此时OP、 AQ的长可依次表示为t、2t个单位。∴t+2t=10,∴t=。综上,符合题意的 图4 y x B O Q(P) N C D M E F t值分别为,2, 。 x y O A M (C) B (E) D P Q F N 图3 E x O A B C y P M Q N F D 图2 2、(2010年北京市) 25. 问题:已知△ABC中,ÐBAC=2ÐACB,点D是△ABC内的一点,且AD=CD,BD=BA。 探究ÐDBC与ÐABC度数的比值。 请你完成下列探究过程: 先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。 A C B (1) 当ÐBAC=90°时,依问题中的条件补全右图。 观察图形,AB与AC的数量关系为 ; 当推出ÐDAC=15°时,可进一步推出ÐDBC的度数为 ; 可得到ÐDBC与ÐABC度数的比值为 ; (2) 当ÐBAC¹90°时,请你画出图形,研究ÐDBC与ÐABC度数的比值 是否与(1)中的结论相同,写出你的猜想并加以证明。 D A C B 图1 【解答】 25. 解:(1) 相等;15°;1:3。 (2) 猜想:ÐDBC与ÐABC度数的比值与(1)中结论相同。 证明:如图2,作ÐKCA=ÐBAC,过B点作BK//AC交CK于点K, 连结DK。∵ÐBAC¹90°,∴四边形ABKC是等腰梯形, ∴CK=AB,∵DC=DA,∴ÐDCA=ÐDAC,∵ÐKCA=ÐBAC, ∴ÐKCD=Ð3,∴△KCD@△BAD,∴Ð2=Ð4,KD=BD, B A C D K 1 2 3 4 5 6 图2 ∴KD=BD=BA=KC。∵BK//AC,∴ÐACB=Ð6, ∵ÐKCA=2ÐACB,∴Ð5=ÐACB,∴Ð5=Ð6,∴KC=KB, ∴KD=BD=KB,∴ÐKBD=60°,∵ÐACB=Ð6=60°-Ð1, ∴ÐBAC=2ÐACB=120°-2Ð1, ∵Ð1+(60°-Ð1)+(120°-2Ð1)+Ð2=180°,∴Ð2=2Ð1, ∴ÐDBC与ÐAB C度数的比值为1:3。 3、(2010年安徽省芜湖市)23.(本小题满分12分) 如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M点作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点. (1)求证:PM=PN; (2)若BD=4,PA= AO,过点B作BC∥MP交⊙O于C点,求BC的长. 【解答】 解: 4、(2010年安徽省芜湖市)24.(本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′. (1)求折痕所在直线EF的解析式; (2)一抛物线经过B、E、B′三点,求此二次函数解析式; (3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由. 【解答】 5、(2010年安徽省) 22.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售。 九(1)班数学建模兴趣小组根据调查,整理出第天(且为整数)的捕捞与销售的相关信息如下: ⑴在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的? ⑵假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第天的收入(元)与(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本) 试说明⑵中的函数随的变化情况,并指出在第几天取得最大值,最大值是多少? 【解答】 6、(2010年安徽省)23.如图,已知△ABC∽△,相似比为(),且△ABC的三边长分别为、、(),△的三边长分别为、、。 ⑴若,求证:; ⑵若,试给出符合条件的一对△ABC和△,使得、、和、、进都是正整数,并加以说明; ⑶若,,是否存在△ABC和△使得?请说明理由。 【解答】 7、(2010年福建省德化县)25、(12分)在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0<α<120°),得△A1BC1,交AC于点E,AC分别交A1C1、BC于D、F两点. (1)如图①,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论; (2)如图②,当=30°时,试判断四边形BC1DA的形状,并说明理由; (3)在(2)的情况下,求ED的长. C1 A1 F E D C B A 图① C1 A1 F E D C B A 图② 【解答】 25、(1);提示证明……………3分 (2)①菱形(证明略)………………………………………7分 (3)过点E作EG⊥AB,则AG=BG=1 在中, 由(2)知AD=AB=2 ∴……………12分 8、(2010年福建省德化县)26、(12分)如图1,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3. (1)求该抛物线的函数关系式; (2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示). ① 当t=时,判断点P是否在直线ME上,并说明理由; 图2 B C O A D E M y x P N · 图1 B C O (A) D E M y x ② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由. 【解答】 26、解:(1)……………3分 (2)①点P不在直线ME上…………………7分 ②依题意可知:P(,),N(,) 当时,以P、N、C、D为顶点的多边形是四边形PNCD,依题意可得: =+=+= = ∵抛物线的开口方向:向下,∴当=,且时,= 当时,点P、N都重合,此时以P、N、C、D为顶点的多边形是三角形 依题意可得,==3 综上所述,以P、N、C、D为顶点的多边形面积S存在最大值.………12分 9、(2010年福建省福州市)21.(满分13分) 如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H。 (1)求证:; (2)设EF=,当为何值时,矩形EFPQ的面积最大?并求其最大值; (3)当矩形EFPQ的面颊最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式。 【解答】 10、(2010年福建省福州市)22.(满分14分) 如图1,在平面直角坐标系中,点B在直线上,过点B作轴的垂线,垂足为A,OA=5。若抛物线过点O、A两点。 (1)求该抛物线的解析式; (2)若A点关于直线的对称点为C,判断点C是否在该抛物线上,并说明理由; (3)如图2,在(2)的条件下,⊙O1是以BC为直径的圆。过原点O作O1的切线OP,P为切点(P与点C不重合),抛物线上是否存在点Q,使得以PQ为直径的圆与O1相切?若存在,求出点Q的横坐标;若不存在,请说明理由。 【解答】 11、(2010年福建省晋江市)25.(13分)已知:如图,把矩形放置于直角坐标系中,,,取的中点,连结,把沿轴的负方向平移的长度后得到. (1)试直接写出点的坐标; (2)已知点与点在经过原点的抛物线上,点在第一象限内的该抛物线上移动,过点作轴于点,连结. ①若以、、为顶点的三角形与相似,试求出点的坐标; ②试问在抛物线的对称轴上是否存在一点,使得的值最大. A O x B C M y 【解答】 25.(本小题13分) A O x D B C M y E P T Q 解:(1)依题意得:;………(3分) (2) ① ∵,,∴. ∵抛物线经过原点, ∴设抛物线的解析式为 又抛物线经过点与点 ∴ 解得: ∴抛物线的解析式为.…………………(5分) ∵点在抛物线上, ∴设点. 1)若∽,则, ,解得:(舍去)或, ∴点.………………………………………………………………(7分) 2)若∽,则, ,解得:(舍去)或, ∴点.……………………………………………………………………(9分) ②存在点,使得的值最大. 抛物线的对称轴为直线,设抛物线与轴的另一个交点为,则点.………………………………………………………………………(10分) ∵点、点关于直线对称, ∴……………………………………………………………………(11分) 要使得的值最大,即是使得的值最大, 根据三角形两边之差小于第三边可知,当、、三点在同一直线上时,的值最大. ……………………………………………………………………………(12分) 设过、两点的直线解析式为, ∴ 解得: ∴直线的解析式为. 当时,. ∴存在一点使得最大.………………………(13分) 12、(2010年福建省晋江市)26.(13分)如图,在等边中,线段为边上的中线. 动点在直线上时,以为一边且在的下方作等边,连结. (1) 填空:度; (2) 当点在线段上(点不运动到点)时,试求出的值; (3)若,以点为圆心,以5为半径作⊙与直线相交于点、两点,在点运动的过程中(点与点重合除外),试求的长. A B C 备用图(1) A B C 备用图(2) 【解答】 26.(本小题13分) (1)60;…………………………………………(3分) (2)∵与都是等边三角形 ∴,, ∴ ∴……………………………(5分) ∴≌ ∴,∴.………………………(7分) (3)①当点在线段上(不与点重合)时,由(2)可知≌,则,作于点,则,连结,则. 在中,,,则. 在中,由勾股定理得:,则.………………………(9分) ②当点在线段的延长线上时,∵与都是等边三角形 ∴,, ∴ ∴ ∴≌ ∴,同理可得:.…………………………(11分) ③当点在线段的延长线上时, ∵与都是等边三角形 ∴,, ∴ ∴ ∴≌ ∴ ∵ ∴ ∴. 同理可得:. 综上,的长是6. ………………………(13分) 13、(2010年福建省龙岩市)24.(13分) 在平面直角坐标系中,点A、B的坐标分别为(10,0),(2,4). (1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的解析式; (2)若P为抛物线上异于C的点,且△OAP是直角三角形,请直接写出点P的坐标; (3)若抛物线顶点为D,对称轴交x轴于点M,探究:抛物线对称轴上是否存在异于D的 点Q,使△AQD是等腰三角形,若存在,请求出点Q的坐标;若不存在,请说明理由. 【解答】 则结合图形,可求得满足条件的Q点坐标为(5,),(5,) 记为Q2(5,),Q3(5,); …………11分 若 则设Q(5,y),由 解得y=, 所以满足条件的Q点坐标为(5,),记为Q4(5,)…12分 所以,满足条件的点Q有 Q1(5,),,, ……13分 14、(2010年福建省龙岩市)25.(14分) 如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C逆时针旋转角(),得到Rt△,与AB交于点D,过点D作DE∥交于 点E,连结BE.易知,在旋转过程中,△BDE为直角三角形. 设 BC=1,AD=x,△BDE的 面积为S. (1)当时,求x的值. (2)求S与x 的函数关系式,并写出x的取值范围; (3)以点E为圆心,BE为半径作⊙E,当S=时,判断⊙E与的位置关 系,并求相应的值. 【解答】 过D作于,则, ∴ ∴. ………12分 ②当时,, ∴ ∴ ∴此时与相交. ……13分 同理可求出. ………14分 15、(2010年福建省南安市)25.(13分) 某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为且过顶点C(0,5)(长度单位:m) (1)直接写出c的值; (2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元 / ,求购买地毯需多少元? (3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°) 【解答】 25.(本小题13分) 解(1)c=5.……………………………3分 (2)由(1)知,OC=5,…………………………4分 令,即,解得.…………5分 ∴地毯的总长度为:,………………6分 ∴(元). 答:购买地毯需要900元.……………………7分 (3)可设G的坐标为,其中, 则. ………………………………………8分 由已知得:, 即,………………………………………9分 解得:(不合题意,舍去).………………………10分 把代入 . ∴点G的坐标是(5,3.75).…………………………………… ……11分 ∴. 在Rt△EFG中,,……………12分 ∴.…………………13分 16、(2010年福建省南安市)26.(13分)如图1,在中,,,,另有一等腰梯形()的底边与重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点. (1)直接写出△AGF与△ABC的面积的比值; (2)操作:固定,将等腰梯形以每秒1个单位的速度沿方向向右运动,直到点与点重合时停止.设运动时间为秒,运动后的等腰梯形为(如图2). ①探究1:在运动过程中,四边形能否是菱形?若能,请求出此时的值;若不能,请说明理由. F G A B D C E 图2 ②探究2:设在运动过程中与等腰梯形重叠部分的面积为,求与的函数关系式. A F G (D)B C(E) 图1 【解答】 26.(本小题13分) 解:(1)△AGF与△ABC的面积比是1:4.………………………3分 (2)①能为菱形.……………………4分 由于FC∥,CE∥, 四边形是平行四边形.…………………………5分 当时,四边形为菱形,………………… 6分 此时可求得. 当秒时,四边形为………… 7分 ②分两种情况: A F G (D)B C(E) 图3 M ①当时, 如图3过点作于. ,,,为中点, . 又分别为的中点, .…………………… 8分 方法一: 等腰梯形的面积为6. ,.…………… …………… 9分 重叠部分的面积为:. 当时,与的函数关系式为.………………10分 方法二: ,,,………… ……… 9分 重叠部分的面积为: . F G A B C E 图4 Q D P 当时,与的函数关系式为.………………10分 ②当时, 设与交于点, 则. ,, 作于,则.……………11分 重叠部分的面积为: . 综上,当时,与的函数关系式为;当时, …………………13分 17、(2010年福建省南平市)25.(14分)如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA; (2)□APCD是否为矩形?请说明理由; (3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论. 图1 A B D C E P 图2 A B D C E P M N F 【解答】 25、(1)证明:在ΔABC和ΔAEP中 ∵∠ABC=∠AEP,∠BAC=∠EAP ∴ ∠ACB=∠APE 在ΔABC中,AB=BC ∴∠ACB=∠BAC ∴ ∠EPA=∠EAP (2) 答:□ APCD是矩形 ∵四边形APCD是平行四边形 ∴ AC=2EA, PD=2EP ∵ 由(1)知 ∠EPA=∠EAP ∴ EA=EP 则 AC=PD ∴□APCD是矩形 (3) 答: EM=EN ∵EA=EP ∴ ∠EPA=90°- α ∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+ α 由(2)知∠CPB=90°,F是BC的中点,∴ FP=FB ∴∠FPB=∠ABC=α ∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α ∴ ∠EAM=∠EPN ∵ ∠AEP绕点E顺时针旋转适当的角度,得到∠MEN ∴ ∠AEP=∠MEN ∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP ∴ ΔEAM≌ΔEPN ∴ EM=EN 18、(2010年福建省南平市)26.(14分)如图1,已知点B(1,3)、C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD. (1)填空:A点坐标为(____,____),D点坐标为(____,____); (2)若抛物线y= x2+bx+c经过C、D两点,求抛物线的解析式; (3)将(2)中的抛物线沿y轴向上平移,设平移后所得抛物线与y轴交点为E,点M是平移后的抛物线与直线AB的公共点,在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由. (提示:抛物线y=ax2+bx+c(a≠0)的对称轴是x=-,顶点坐标是(-,) O y x A D B C 图1 O y x A B C 备用图 · 【解答】 26. 解:(1) A(-2,0) ,D(-2,3) (2)∵抛物线y= x2+bx+c 经过C(1,0), D(-2,3) 代入,解得:b=- ,c= ∴ 所求抛物线解析式为:y= x2 - x+ (3) 答:存在 解法一: 设抛物线向上平移H个单位能使EM∥x轴, 则平移后的解析式为:y= x2 - x++h =(x -1)² + h 此时抛物线与y轴交点E(0,+h) 当点M在直线y=x+2上,且满足直线EM∥x轴时 则点M的坐标为() 又 ∵M在平移后的抛物线上,则有 +h=(h--1)²+h 解得: h= 或 h= (і)当 h= 时,点E(0,2),点M的坐标为(0,2)此时,点E,M重合,不合题意舍去。 (ii)当 h=时,E(0,4)点M的坐标为(2,4)符合题意 综合(i)(ii)可知,抛物线向上平移个单位能使EM∥x轴。 解法二:∵当点M在抛物线对称轴的左侧或在抛物线的顶点时,仅当M,E重合时,它们的纵坐标相等。 ∴EM不会与x轴平行 当点M在抛物线的右侧时,设抛物线向上平移H个单位能使EM∥x轴 则平移后的抛物线的解析式为∵y=x²++h =(x - 1)² + h ∴ 抛物线与Y轴交点E(0,+h) ∵抛物线的对称轴为:x=1 根据抛物线的对称性,可知点M的坐标为(2,+h)时,直线EM∥x轴 将(2,+h)代入y=x+2得,+h=2+2 解得:h= ∴ 抛物线向上平移个单位能使EM∥x轴 19、(2010年福建省宁德市)25.(本题满分13分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM. E A D B C N M ⑴ 求证:△AMB≌△ENB; ⑵ ①当M点在何处时,AM+CM的值最小; ②当M点在何处时,AM+BM+CM的值最小,并说明理由; ⑶ 当AM+BM+CM的最小值为时,求正方形的边长. 【解答】 25.(满分13分)解:⑴∵△ABE是等边三角形, F E A D B C N M ∴BA=BE,∠ABE=60°. ∵∠MBN=60°, ∴∠MBN-∠ABN=∠ABE-∠ABN. 即∠BMA=∠NBE. 又∵MB=NB, ∴△AMB≌△ENB(SAS). ………………5分 ⑵①当M点落在BD的中点时,AM+CM的值最小. ………………7分 ②如图,连接CE,当M点位于BD与CE的交点处时, AM+BM+CM的值最小. ………………9分 理由如下:连接MN.由⑴知,△AMB≌△ENB, ∴AM=EN. ∵∠MBN=60°,MB=NB, ∴△BMN是等边三角形. ∴BM=MN. ∴AM+BM+CM=EN+MN+CM. ………………10分 根据“两点之间线段最短”,得EN+MN+CM=EC最短 ∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.……11分 ⑶过E点作EF⊥BC交CB的延长线于F, ∴∠EBF=90°-60°=30°. 设正方形的边长为x,则BF=x,EF=. 在Rt△EFC中, ∵EF2+FC2=EC2, ∴()2+(x+x)2=. ………………12分 解得,x=(舍去负值). ∴正方形的边长为. ………………13分 20、(2010年福建省宁德市)26.(本题满分13分)如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0). ⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______; ⑵若△EFG与梯形ABCD重叠部分面积是y,求 ①当0<x≤2时,y与x之间的函数关系式; ②当2<x≤6时,y与x之间的函数关系式; B E→ F→ C A D G ⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值. 【解答】 26.(满分13分)解:⑴ x,D点;………………3分 ⑵ ①当0<x≤2时,△EFG在梯形ABCD内部,所以y=x2;………………6分 ②分两种情况: Ⅰ.当2<x<3时,如图1,点E、点F在线段BC上, △EFG与梯形ABCD重叠部分为四边形EFNM, ∵∠FNC=∠FCN=30°,∴FN=FC=6-2x.∴GN=3x-6. 由于在Rt△NMG中,∠G=60°, 所以,此时 y=x2-(3x-6)2=.………………9分 Ⅱ.当3≤x≤6时,如图2,点E在线段BC上,点F在射线CH上, △EFG与梯形ABCD重叠部分为△ECP, ∵EC=6-x, ∴y=(6-x)2=.………………11分 ⑶当0<x≤2时,∵y=x2在x>0时,y随x增大而增大, ∴x=2时,y最大=; 当2<x<3时,∵y=在x=时,y最大=; 当3≤x≤6时,∵y=在x<6时,y随x增大而减小, ∴x=3时,y最大=.………………12分 B E C F A D G P H 图2 综上所述:当x=时,y最大=.………………13分 B E F C A D G N M 图1 21、(2010年福建省莆田市)24.(本小题满分12分) 如图1,在Rt中,点D在边AB上运动,DE平分交边BC于点E,垂足为,垂足为N. 第24题 (1)当AD=CD时,求证:; (2)探究:AD为何值时,与相似? (3)探究:AD为何值时,四边形MEND与的面积相等? 24.(本小题满分12分) 第24题 (1)证明: 1分 又∵DE是∠BDC的平分线 ∴∠BDC=2∠BDE ∴∠DAC=∠BDE 2分 ∴DE∥AC 3分 (2)解:(Ⅰ)当时,得 ∴BD=DC ∵DE平分∠BDC ∴DE⊥BC,BE=EC. 又∠ACB=90° ∴DE∥AC. 4分 ∴即 ∴AD=5 5分 (Ⅱ)当时,得 ∴EN∥BD 又∵EN⊥CD ∴BD⊥CD即CD是△ABC斜边上的高 6分 由三角形面积公式得AB·CD=AC·BC ∴CD= ∴ 7分 综上,当AD=5或时,△BME与△CNE相似. (3)由角平分线性质易得 即 8分 ∴EM是BD的垂直平分线. 第24题 ∴∠EDB=∠DBE ∵∠EDB=∠CDE ∴∠DBE=∠CDE 又∵∠DCE=∠BCD ∴ 9分 10分 即 11分 由式得 12分 22、(2010年福建省莆田市)25.(本小题满分14分) 如图1,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且. (1)求直线AC的解析式; (2)在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由. 第25题 (3)抛物线经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且沿DE折叠后点O落在边AB上处? 【解答】 25.(本小题满分14分) 解:(1)OA=1,OC=2 则A点坐标为(0,1),C点坐标为(2,0) 设直线AC的解析式为y=kx+b 解得 直线AC的解析式为 2分 (2)或 (正确一个得2分) 8分 第25题 (3)如图,设 过点作于F 由折叠知 或2 10分 23、(2010年福建省泉州市)25.(12分)我们容易发现:反比例函数的图象是一个中心对称图形.你 可以利用这一结论解决问题. 如图,在同一直角坐标系中,正比例函数的图象可以看作是:将轴所在的直线绕着原点逆时针旋转α度角后的图形.若它与反比例函数的图象分别交于第一、三象限的点、,已知点、. (1)直接判断并填写:不论α取何值,四边形的形状一定是 ; (2)①当点为时,四边形是矩形,试求、α、和有值; ②观察猜想:对①中的值,能使四边形为矩形的点共有几个?(不必说理) (3)试探究:四边形能不能是菱形?若能, 直接写出B点的坐标, 若不能, 说明理由. 【解答】 25.(本小题12分) 解:(1)平行四边形 …………(3分) (2)①∵点在的图象上,∴ ∴………………………………(4分) 过作,则 在中, α=30° ……………………………………………………………(5分) ∴ 又∵点B、D是正比例函数与反比例函数图象的交点, ∴点B、D关于原点O成中心对称 ………………………………………(6分) ∴OB=OD= ∵四边形为矩形,且 ∴………………………………………………………(7分) ∴; ……………………………………………………………(8分) ②能使四边形为矩形的点B共有2个; ………………………………(9分) (3)四边形不能是菱形. ……………………………………………(10分) 法一:∵点、的坐标分别为、 ∴四边形的对角线在轴上. 又∵点、分别是正比例函数与反比例函数在第一、三象限的交点. ∴对角线与不可能垂直. ∴四边形不能是菱形 法二:若四边形ABCD为菱形,则对角线AC⊥BD,且AC与BD互相平分, 因为点A、C的坐标分别为(-m,0)、(m,0) 所以点A、C关于原点O对称,且AC在x轴上. ……………………………………(11分) 所以BD应在y轴上,这与“点B、D分别在第一、三象限”矛盾, 所以四边形ABCD不可能为菱形. ……………………………………………………(12分) 24、(2010年福建省泉州市)26. (14分)如图所示,已知抛物线的图象与轴相交于点 ,点在该抛物线图象上,且以为直径的⊙恰 好经过顶点. (1)求的值; (2)求点的坐标; (3)若点的纵坐标为,且点在该抛物线的对称轴上运动,试探 索: ①当时,求的取值范围(其中:为△的面积,为△的面积,为四边 形OACB的面积); ②当取何值时,点在⊙上.(写出的值即可) 【解答】 26.(本小题14分) 解:(1)∵点B(0,1)在的图象上,∴………………(2分) ∴k=1………………(3分) (2)由(1)知抛物线为: ∴顶点A为(2,0) …………(4分) ∴OA=2,OB=1 过C(m,n)作CD⊥x轴于D,则CD=n,OD=m,∴AD=m-2 由已知得∠BAC=90° …………………(5分) ∴∠CAD+∠BAO=90°,又∠BAO+∠OBA=90°∴∠OBA=∠CAD ∴Rt△OAB∽Rt△DCA ∴(或tan∠OBA= tan∠CAD )…(6分) ∴n=2(m-2); 又点C(m,n)在上,∴ ∴,即 ∴m=2或m=10;当m=2时,n=0, 当m=10时,n=16;…………………(7分) ∴符合条件的点C的坐标为(2,0)或(10,16)…(8分) (3)①依题意得,点C(2,0)不符合条件,∴点C为(10,16) 此时 ……………………………… (9分) t 又点P在函数图象的对称轴x=2上,∴P(2,t),AP= t ∴= ……………………………(10分) ∵ ∴当t≥0时,S=t,∴1﹤t﹤21. ………………(11分) ∴当t﹤0时,S=-t,∴-21﹤t﹤-1 ∴t的取值范围是:1﹤t﹤21或-21﹤t﹤-1 …………(12分) ②t=0,1,17. ……………………………………(14分) 25、(2010年福建省漳州市)25.(满分13分)如图,在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P、Q分别从A、C两点同时出发,其中点P以1cm/s的速度沿AC向终点C移动;点Q以cm/s的速度沿CB向终点B移动.过P作PE∥CB交AD于点E,设动点的运动时间为x秒. (1)用含 x的代数式表示EP; (2)当Q在线段CD上运动几秒时,四边形PEDQ是平行四边形; (3)当Q在线段BD(不包括点B、点D)上运动时,求四边形EPDQ面积的最大值. 【解答】 25.解:(1)∵PE∥CB,∴∠AEP=∠ADC 又∵∠EAP=∠DAC,∴△AEP∽△ADC ……………………………………2分 ∴,∴…………3分 ∴.…………………………4分 (2)由四边形PEDQ1是平行四边形, 可得EP=DQ1.………………………5分 即, 所以.…………………………6分 ∵0 < x < 2.4……………………………7分 ∴当Q在线段CD上运动1.5秒时,四边形PEDQ是平行四边形.……8分 (3)……………………9分 ………………………………10分 又∵2.4 < x < 4,………………………………………………12分 ∴当时,S取得最大值,最大值为.………………13分 26、(2010年福建省漳州市)26.(满分14分)如图,直线分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△DOC,抛物线经过A、B、C三点. (1)填空:A( , )、B( , )、C( , ); (2)求抛物线的函数关系式; (3)E为抛物线的顶点,在线段DE上是否存在点P,使得以C、D、P为顶点的三角形与△DOC相似?若存在,请求出点P的坐标;若不存在,请说明理由. 【解答】 26.(满分14分) (1)A(-1,0),B(0,-3),C(3,0)……………………………………3分 (2)∵抛物线经过B点,∴c=-3. 又∵抛物线经过A,C两点,∴解得………………5分 ∴……………………………………………………………………6分 (3)解:过点E作EF⊥y轴垂足为点F. 由(2)得 ∴E(1,—4)。 ∵tan∠EDF=,tan∠DCO=. ∴∠EDF=∠DCO………………………7分 ∵∠DCO+∠ODC=90°, ∴∠EDF+∠ODC=90°. ∴∠EDC=90°, ∴∠EDC=∠DOC.……………………8分 ① 当时,△ODC∽△DPC, 则,∴DP=…………………9分 过点P作PG⊥y轴,垂足为点G. ∵tan∠EDF=,∴设PG=x,则DG=3x 在Rt△DGP中,DG2+PG2=DP2. ∴,∴(不合题意,舍去)………………10分 又∵OG=DO+DG=1+1=2,∴P(,).…………………………………11分 ① 当时,△ODC∽△DCP,则∴DP=. ∵DE=,∴DP=(不合题意,舍去)…………13分 综上所述,存在点P,使得以C、D、P为顶点的三角形与△DOC相似,此时点P的坐标为P(,).……………………………………………………14分查看更多