中考数学图形认识初步一轮复习

中考数学图形认识初步一轮复习

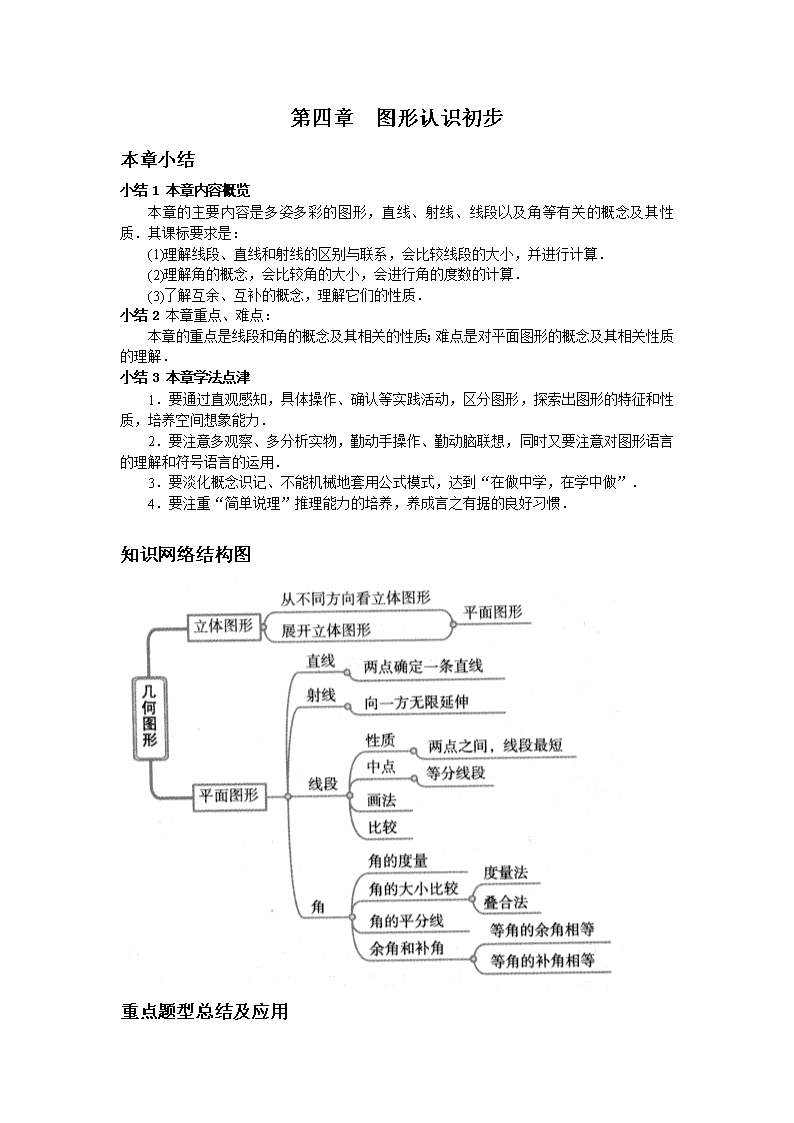
第四章 图形认识初步 本章小结 小结1 本章内容概览 ‎ 本章的主要内容是多姿多彩的图形，直线、射线、线段以及角等有关的概念及其性质．其课标要求是：‎ ‎ (1)理解线段、直线和射线的区别与联系，会比较线段的大小，并进行计算．‎ ‎ (2)理解角的概念，会比较角的大小，会进行角的度数的计算．‎ ‎ (3)了解互余、互补的概念，理解它们的性质．‎ 小结2 本章重点、难点：‎ 本章的重点是线段和角的概念及其相关的性质；难点是对平面图形的概念及其相关性质的理解．‎ 小结3 本章学法点津 ‎ ‎ 1．要通过直观感知，具体操作、确认等实践活动，区分图形，探索出图形的特征和性质，培养空间想象能力． ‎ ‎ 2．要注意多观察、多分析实物，勤动手操作、勤动脑联想，同时又要注意对图形语言的理解和符号语言的运用． ‎ ‎ 3．要淡化概念识记、不能机械地套用公式模式，达到“在做中学，在学中做”．‎ ‎ 4．要注重“简单说理”推理能力的培养，养成言之有据的良好习惯．‎ 知识网络结构图 重点题型总结及应用 题型一 计算几何图形的数量 ‎ ‎1．数直线条数 ‎ 例1 已知n(n≥2)个点P1，P2，P3，…，Pn在同一平面上，且其中没有任何三点在同一直线上．设Sn表示过这n个点中的任意2个点所作的所有直线的条数，显然，S2=1，S3＝3，S4＝6，S6＝10，…，由此推断，Sn＝ .‎ ‎ 答案：‎ ‎ 点拨 经过第一个点可以引出(n－1)条直线，经过第二个点可以新引出(n－2)条直线，经过第三个点可以新引出(n－3)条直线，…，所以n个点一共可以引出Sn＝ (n－1)＋(n－2)＋(n－3)＋…＋1＝条直线．‎ ‎2．数线段条数 ‎ 例2 如图4—4—1所示，C、D为线段AB上的任意两点，那么图中共有多少条线段?‎ 解：按照从左到右的顺序去数线段条数，以A为一个端点的线段有3条：AC、AD、AB；以C为一个端点的新线段有2条：CD、CB；以D为一个端点的新线段有1条：DB．所以共有线段3＋2＋1＝6(条)．‎ 点拨 线段的条数与线段上固定点(包括线段两个端点)的个数有密切联系，线段上有n 个点(包括线段两个端点)时，共有线段条．‎ ‎ 例3 小明在看书时发现这样一个问题：在一次聚会中，共有6人参加，如果每两人都握一次手，共握几次手呢?小明通过认真思考得出了答案．为了解决一般问题，小明设计了下列图表进行探究：‎ 参加人数 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎…‎ 握手示 意图 握手次数 ‎1‎ ‎2＋1=3‎ ‎3＋2＋1=6‎ ‎4＋3＋2＋1=10‎ ‎…‎ ‎ 请你根据上面图表归纳出参加人数与握手次数之间关系的一般结论．‎ ‎ 分析：本题研究的是握手次数问题，但可以将此问题转化成研究平面上的点构成线段的条数问题．这里把每个人看作一个点，根据图表中的信息，通过探究推理可得到问题的答案．‎ ‎ 解：若有6人参加，则共握手15次．‎ 结论：若有n(n≥2，且n为整数)人参加，则共握手(n－1)＋(n－2)＋(n－3)＋…＋4＋3＋2＋1＝ (次)．‎ 点拨 解决此类问题的关键是将实际问题抽象转化为平面图形的具体计数问题。再进行探究． ‎ ‎3．数直线分平面的块数 ‎ 例4 豆腐是我们生活中的常见食品，常被分割成长方体或正方体的小块出售．现请你用刀切豆腐，每次切三刀，能将豆腐切成多少块?‎ ‎ 分析：这三刀可以随意切，不要拘泥于规范、常见切法．从不同的角度下手，得到的小块豆腐的块数可能不同．‎ 解：如图4—4—2所示，能将豆腐切成4块、6块、7块或8块．‎ 点拨 在截一个几何体之前应充分想象截面可能的形状，然后实际操作，在比较想象结果与实际结果的差异的过程中，可以丰富我们的几何直觉，积累数学活动经验，同时培养我们的空间观察能力．‎ 题型二 两角互补、互余定义及其性质的应用 ‎ 例5 一个角的补角是这个角的4倍，求这个角的度数．‎ 解：设这个角是x°，则它的补角是(180－x)°．‎ 由题意，得180－x＝4 x，解得x＝36．所以这个角是36°．‎ 点拨 ‎ 本题主要考查补角定义的应用，数学中利用方程、转化思想，可将“形”的问题转化为“数”的问题研究，从而简捷解决问题． ‎ ‎ 例6 如果一个角的补角是120°，那么这个角的余角是( )‎ ‎ A．30° B．60° C．90° D．150°‎ ‎ 解析：本题是对余角、补角的综合考查，先根据这个角的补角是120°，求出这个角是60°，再求出它的余角是30°． 答案：A ‎ 例7 根据补角的定义和余角的定义可知，10°的角的补角是170°，余角是80°；15°的角的补角是165°，余角是75°；32°的角的补角是148°，余角是58°．…. 观察以上各组数据，你能得出怎样的结论?请用任意角α代替题中的10°、15°、32°的角来说明你的结论．‎ ‎ 解：结论为：一个角的补角比这个角的余角大90°．‎ ‎ 说明：设任意角是α(0＜α＜90°)，α的补角是180°－α，α的余角是90°－α，‎ 则 (180°－α)－(90°－α)＝90°.‎ 题型三 角的有关运算 ‎ 例8 如图4—4—3所示，AB和CD都是直线，∠AOE＝90°，∠3°=∠FOD，∠1＝27°20′，求∠2、∠3的度数．‎ ‎ 解：因为∠AOE＝90°，‎ ‎ 所以∠2＝90°－∠1＝90°－27°20′＝62°40′．‎ ‎ 又因为∠AOD＝180°－∠1＝152°40′，∠3＝∠FOD，‎ ‎ 所以∠3＝∠AOD＝76°20′．‎ ‎ 所以上2＝62°40′，∠3＝76°20′．‎ ‎ 例9 如图4—4—4所示，OB、OC是∠AOD内任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON＝α，∠BOC=β ‎，用α、β表示∠AOD．‎ ‎ 解：因为∠MON＝α，∠BOC=β，‎ ‎ 所以∠BOM＋∠CON＝∠MON－∠BOC=α－β ‎ 又OM平分∠AOB，ON平分∠COD，‎ ‎ 所以∠AOB＋∠COD＝2∠BOM＋2∠CON ‎ =2(∠BOM＋∠CON)＝2(α－β)，‎ ‎ 所以∠AOD＝∠AOB＋∠COD＋∠BOC＝2(α－β)＋β=2α－β.‎ ‎ 例10 (1)用度、分、秒表示54．12°．‎ ‎ (2)32°44′24″等于多少度?‎ ‎ (3)计算：133°22′43″÷3．‎ ‎ 解：(1)因为0．12°＝60′×0．12=7．2′，0.2′=60″×0．2=12″，‎ ‎ 所以54．12°=54°7′12″．‎ ‎ (2)因为24″=()′×24＝0．4′，44．4′=()°×44．4=0．74°，‎ ‎ 所以32°44′24″=32.74°．‎ ‎ (3)133°22′43″÷3＝(132°＋82′)÷3＋43″÷3=44°＋82′÷3＋43″÷3‎ ‎ ＝44°＋(81′＋1′)÷3＋43″÷3=44°＋27′＋1′÷3＋43″÷3‎ ‎=44°＋27′＋103″÷3≈44°＋27′＋3″=44°27′3″.‎ 方法总结 角的有关运算是指角的单位换算和角的加、减、乘、除运算．角度制的单位是 60进制的，和计量时间的时、分、秒一样．加减时，要将度、分、秒分别相加、相减，分、秒逢60要进位，而相减不够时要借1作60；度、分、秒形式乘一个数时，要将度、分、秒分别乘这个数，分、秒逢60进位；度、分、秒形式除以一个数时，也是将度、分、秒分别除以这个数，不过要将高位的余数转化成低位，与原位上的数相加后再除以这个数．‎ 题型四 钟表的时针与分针夹角问题 例11 15：25时钟面上时针和分针所构成的角是 度．‎ 解析：起始时刻定为15：00(下午3点整时，时针和分针构成的角是90°)，终止时刻为15：25，从图4—4—5中可以看出分针从12转到5用了25分钟，转了6°×25＝150°，时针转了0．5°×25＝12．5°，所以15：25时钟面上时针和分针所构成的角为150°－90°－ 12．5°＝47．5°． 答案：47．5‎ 点拨 解决此类问题时要选择恰当的起始时刻，注意时针和分针同时在运动，并牢记时针每分钟转＝o．5=0.5，分针每分钟转＝6°．‎ 题型五 图形的转化 例12 下列图形中不是正方体的平面展开图的是( )‎ 解析：通过折叠验证四个选项，可得正确答案． 答案：C 点拨 ‎ ‎ 立体图形的平面展开图是沿着立体图形的一些棱将它剪开，把立体图形展开成一个平面图形．一个正方体的平面展开图中，在同一直线上相邻的三个正方形中，首尾两个正方形是正方体中相对的两个面．‎ 例13 如图4—4—6所示，将标号为A、B、C、D的正方形沿图中虚线剪开后，得到标号为P、Q、M、N的四组图形，试按照“哪个正方形剪开后得到哪组图形”的对应关系填空：A与 对应；B与 对应；C与 对应；D与 对应．‎ 解析：按照剪开的形状，找出对应的图形． 答案：M，P，Q，N 题型六 方位角 ‎ 例14 如图4—4—7所示，我海军的两艘军舰(分别在A、B两处)同时发现了一艘敌舰，其中A舰发现它在北偏东15°的方向上，B舰发现它在东北方向上，试画出这艘敌舰的位置(用字母C表示)．‎ 解：如图4—4—8所示，分别以点A、点B为中心建立方位图，表示东北方向的射线 BE与表示北偏东15°方向的射线AD的交点C即为这艘敌舰的位置．‎ 点拨 利用角度来描述方位，以正北、正南的方向为基准，先确定是北还是南，然后确定东、西方向，最后确定偏东(或西)的角度，注意东北方向是北偏东45°．‎ 思想方法归纳 ‎ ‎1．分类讨论思想 ‎ 分类讨论，就是对问题所给对象的条件、结论、图形等不能进行统一研究时，就需要将研究对象按某个标准分类，然后对每一类分别研究得出每一类的结论，最后综合各类结果得到整个问题的解答．注意分类时要做到按同一标准且不重不漏．‎ ‎ 例1 已知线段AB＝‎8cm，在直线AB上画线段BC，使它等于‎3cm，求线段AC的长．‎ ‎ 解：本题分两种情况：‎ ‎ 如图4—4—9所示，当点C在线段AB的延长线上时，‎ ‎ AC＝AB＋BC＝8＋3＝11(crn)；‎ ‎ 如图4—4—10所示，当点C在线段AB上时，‎ ‎ AC=AB－BC＝8—3＝5(cm)．‎ ‎ 所以线段AC的长为‎11 cm或‎5cm.‎ ‎ 例2 经过任意三点中的两点共可以画出的直线条数是( )‎ ‎ A．1或3 B．‎3 C．2 D．1‎ 解析：这道题要分两种情况考虑：一是这三点都在一条直线上时，就只能画出一条直线；二是这三点不在同一条直线上时，此时共可以画出三条直线． 答案：A ‎2．数形结合思想 数形结合思想就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”，即通过抽象思维与形象思维的结合，可以使复杂问题简单化、抽象问题具体化，从而起到优化解题途径的目的，线段、直线、角的重要性质也都是通过数形结合的思想体现的．‎ ‎ 例3 如图4—4—11所示放置的三角板，把三角板较长的直角边从水平状态开始，在平面上沿着直线BC滚动一周，求B点转动的角度．‎ 解：三角板转动的路线如图4—4—12所示．由图可知第一次转动90°，第二次转动 120°，第三次没动，所以B点转动了210°．‎ 点拨 解决本题的关键是明确角的变化情况，因此，可根据题意画出从起点到终点转动一圈的示意图，然后根据图形就很容易确定出B点转动的角度了． ‎ ‎3．转化思想 ‎ 解决一个问题，往往是由未知向已知转化，由陌生向熟悉转化，由复杂向简单转化，转化思想贯穿整个数学学习的始终． ‎ 例4 将下列选项中的平面图形绕直线l旋转一周，可以得到如图4—4—13所示立体图形的是( )‎ ‎ 解析：分析立体图形可知，直线l应为初始旋转的直角梯形垂直于两底的腰所在直线． 答案：B ‎ 点拨 本题主要考查了同学们识别图形的能力．对于类似的图形识别问题我们要能从所给立体图形入手，分析形成它的基本图形，把复杂的立体图形转化为平面图形去认识、解决．‎ 中考热点聚焦 ‎ 考点1 线段 ‎ 考点突破：‎ 线段问题在中考题中一般难度不大，解题时要结合图形，认真分析，问题便会迎刃而解．‎ ‎ 例1 （2011广东佛山，12，3分）已知线段AB=6，若C为AB中点，则AC=　3　．‎ 考点两点间的距离 分析由题意可知，线段AB=6，C为AB中点，所以，AC=BC，即AC=3；‎ 解答解：如图，线段AB=6，C为AB中点，‎ ‎∴AC=BC，∴AC=3．故答案为：3．‎ 点评本题考查了两点间的距离，牢记两点间的中点到两端点的距离相等．‎ ‎（2011广西崇左，5，2分）在修建崇钦高速公路时，有时需要将弯曲的道路改直，依据是　 　．‎ ‎ 考点：线段的性质：两点之间线段最短．‎ ‎ 分析：根据线段的性质：两点之间线段最短解答．‎ ‎ 解答：解：在修建崇钦高速公路时，有时需要将弯曲的道路改直，依据是：两点之间线段最短．‎ 故答案为：两点之间线段最短．‎ ‎ 点评：本题考查了两点之间线段最短的性质，是基础题，比较简单．‎ 如图4—4—14所示，点A、 B、C是直线l上的三个点，图中共有线段的条数是( )‎ ‎ A．1 B．‎2 C．3‎ 解析：图中有线段AB、BC、AC． 答案：C 考点2 余角和补角 ‎ 考点突破：此类题在中考中的考查为基础性题目，一般为选择题或填空题，只要牢记余角和补角的定义，便能准确求解．‎ ‎ 例2 （2011清远，6，3分）已知∠α＝35°，则∠α的余角是（　　）‎ ‎ A.35° B.55° C.65° D.145°‎ 考点：余角和补角.‎ 专题：计算题.‎ 分析：根据互为余角的两个角的和为90度作答．‎ 解答：解：根据定义∠α的余角度数是90°﹣35°＝55°．故选．‎ 点评：本题考查角互余的概念：和为90度的两个角互为余角．属于基础题，较简单．‎ ‎（2011•南通）已知∠α=20°，则∠α的余角等于　70°　．‎ 考点：余角和补角。‎ 分析：若两个角的和为90°，则这两个角互余；根据已知条件可直接求出角α的余角．‎ 解答：解：∵∠α=20°，∴∠α的余角=90°﹣20°=70°．故答案为：70°．‎ 点评：本题考查了余角的定义，解题时牢记定义是关键．‎ ‎ （2011福建福州，5，4分）下列四个角中，最有可能与70°角互补的角是（　　）‎ ‎ A． B． C． D．‎ 考点：余角和补角．‎ 分析：根据互补的性质，与70°角互补的角等于180°﹣70°=110°，是个钝角；看下4个答案，哪个符合即可；‎ 解答：解：根据互补的性质得，70°角的补角为：180°﹣70°=110°，是个钝角；∵答案A．B．C都是锐角，答案D是钝角；∴答案D正确．故选D．‎ 点评：本题考查了角互补的性质，明确互补的两角和是180°，并能熟练求已知一个角的补角．‎ ‎ 例3 如果∠α＝60°，那么∠α的余角的度数是( )‎ ‎ A．30° B．60° C．90° D．120°‎ ‎ 解析：∠α的余角的度数为90°－60°＝30°． 答案：A ‎30°角的补角是( )‎ ‎ A．30°角 B．60°角 C．90°角 D．150°角 解析：30°角的补角度数为180°－30°＝150°． 答案：D 考点3 钟表上的角度问题 ‎ 考点突破：此类题是近几年中考中的热点问题，考查形式为选择题或填空题．解决此类问题需明确：在钟表上，1分钟分针走6°，1小时时针走30°．‎ ‎ 例4 从3时到6时，钟表的时针旋转角的度数是( )‎ ‎ A．30° B．60° C．90° D．120°‎ 解析：从3时到6时共3小时，时针旋转角的度数为30°×3＝90°． 答案：C 考点4 从不同方向看立体图形 ‎ 考点突破：从不同方向看立体图形是中考的热点问题，几乎每套中考题中都会出现，解决问题时应发挥空间想象能力，把立体图形转化为平面图形．‎ 例5如图4—4—15所示四个几何体中，从上面看得到的平面图形是圆的几何体共有( )‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎ 解析：题图中从上面看得到的平面图形是圆的几何体是圆柱和球． 答案：B 例6如图4—4—16所示的几何体是由7个大小相同的小正方体组成的，该几何体从上面看得到的平面图形为( )‎ 答案：C 综合验收评估测试题 一、选择题 ‎1. 下列说法正确的是( )‎ A．平角是一条直线 B．周角是一条射线 C．用2倍的放大镜看‎1 cm的线段，这条线段变成了‎2 cm D．用2倍的放大镜看30°的角，这个角变成了60°‎ ‎2．下列说法正确的是( )‎ A．直线AB与直线BA不是同一条直线 B．线段AB与线段BA不是同一条线段 C．射线OA与射线AO不是同一条射线 D．射线OA与射线AO是同一条射线 ‎3. 如图4—4—17所示，AB＝CD，则AC与BD的大小关系是( )‎ A．AC＞BD B．AC＝BD C．AC＜BD D．不能确定 ‎4. 如果线段AB＝‎6 cm，BC=‎5cm，那么A、C两点间的距离是( )‎ A．‎1 cm B．5．‎5 cm C．‎11 cm D．‎11 cm或‎1 cm ‎5. 若∠α的补角是42°，∠β的余角是52°，则∠α和∠β的大小关系是( )‎ A．∠α＞∠β B．∠α＜∠β C．∠α＝∠β D．不能确定 ‎6. 如图4—4—18所示，∠1＝15°，∠AOC＝90°，B、O、D三点在一条直线上，则∠3等于( )‎ A．75° B．105° C．15° D．165°‎ ‎7. 一个角和它的补角的度数比为1∶8，则这个角的余角为( )‎ A．10° B．20° C．70° D．80°‎ ‎8. 如图4—4—19所示，已知∠AOC＝∠BOD=∠78°，∠BOC＝ 35°，则∠AOD等于( )‎ A．113° B．121° C．156° D．86°‎ 二、填空题 ‎9. 29°30′= 度，18．25°＝ 度 分 秒．‎ ‎10. 15分钟时间，时钟上的时针转了 度，分针转了 度．‎ ‎11. 如图4—4—20所示，由点B观测点A的方向是 ．‎ ‎12. 一个画家有14个棱长为‎1米的正方体，他在地面上把它们摆成如图4—4—21所示的形式，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积为 ． ‎ 三、解答题 ‎13. 请仔细观察如图4—4—22所示的折纸过程，然后回答下列问题：‎ ‎ (1)求∠2的大小．‎ ‎ (2)∠1与∠3有何关系?‎ ‎ (3)∠1与∠AEC，∠3与∠BEF分别有何关系?‎ ‎14. 如图4—4—23所示，已知AC=CD＝DB，AC＝2AM，BN＝BM，如果MN＝‎5cm，求AB、CN的长．‎ ‎15. 如图4—4—24所示，一只蚂蚁从O点出发，沿北偏东30°方向爬行2．‎5 cm，碰到障碍物B后，又沿西北方向爬行‎3 cm到达C处．‎ ‎(1)画出蚂蚁爬行的路线；‎ ‎(2)求∠OBC的度数；‎ ‎(3)测出线段OC的长度(精确到0．‎1 cm)．‎ 答案 ‎1. C 2. C 3. B 4. D 5. A 6. B 7. C 8. B ‎9. 29．5，18，15，0 ‎ ‎10. 7．5，90 ‎ ‎11. 南偏西65° ‎ ‎12. 33平方米 ‎ 13. 解：(1)因为从图中可知∠1＋∠3＝∠2，且∠1＋∠3＋∠2＝180°，‎ ‎ 所以∠2＝×18°＝90°．‎ ‎ (2)因为∠1＋∠3=∠2=90°，所以∠1与∠3互余．‎ ‎ (3)因为∠1＋∠AEC＝180°，所以∠l与∠AEC互补；‎ 同理∠3与∠BEF互补．‎ ‎ 14. 解：因为AC=CD＝DB，所以AB＝‎3AC.‎ ‎ 因为AC=2AM，所以AM＝CM=AC.‎ ‎ 又因为BN=BM，所以BN＝MN＝‎5cm．‎ ‎ 所以AB－AM＝BM＝2MN，‎ ‎ 即‎3AC－AC＝2× 5．‎ ‎ 所以AC＝4(cm)．‎ ‎ 所以AB＝‎3AC＝‎12 cm，‎ ‎ CN=MN—CM＝5－×4＝3(cm)．‎ ‎ 15. 解：(1)蚂蚁爬行的路线如图4—4—25所示．‎ ‎ (2)因为蚂蚁从O点出发沿北偏东30°方向爬行2．‎5 cm到达B处，即∠OBD＝30°，则∠ABO＝60°．‎ ‎ 又因为蚂蚁到达B处后又沿西北方向爬行了‎3 cm，即∠ABC＝45°．‎ ‎ 所以∠OBC＝∠ABO＋∠ABC＝60°＋45°＝105°．‎ ‎(3)用刻度尺测量OC的长约为4．‎4 cm．‎