贵州省遵义航天高级中学2019届高三第四次模拟考试数学（文）试题 Word版含答案

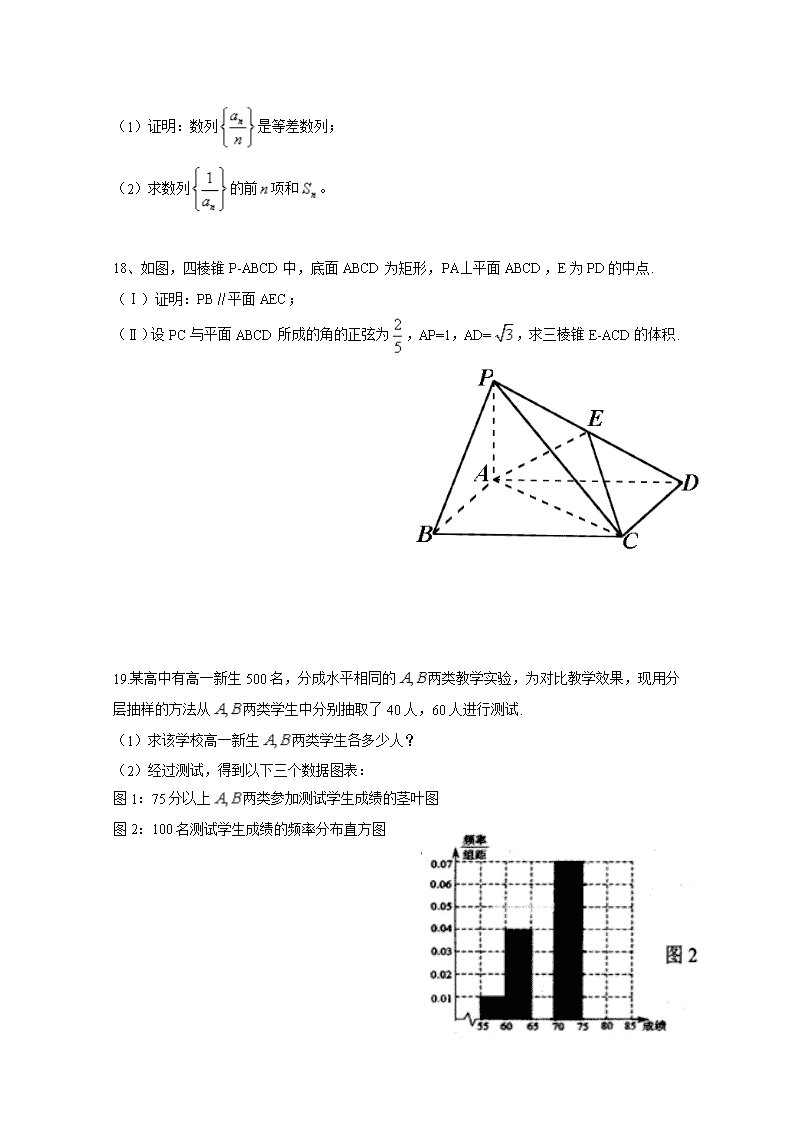
贵州省遵义航天高级中学2019届高三第四次模拟考试数学（文）试题 Word版含答案

高三四模文科数学试题 一、 选择题：‎ 1、 已知集合 ‎ A. ‎ B. C. D.‎ ‎2、已知为虚数单位，则= ‎ A. 1 B. C. D. -1‎ ‎3、已知命题；命题，则.下列命题中为真命题的是 A. B. C. D. ‎ ‎4、已知向量，则下列结论正确的是 A. B.‖ C. D. ‎ 5. 某方便面生产线上每隔15分钟抽取一包进行检验，该抽样方法为①，从某中学的40名数学爱好者中抽取5人了解学习负担情况，该抽样方法为②，那么①和②分别为 A. ①系统抽样，②简单随机抽样 B. ①分层抽样,②系统抽样 C. ①系统抽样, ②分层抽样 D.①分层抽样,②简单随机抽样 ‎6、某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是 A．2 B．4 C．6 D．8‎ ‎7、在等差数列中，若，，则等于（ ） ‎ A.9 B.7 C.6 D.5‎ ‎8、一次数学考试后，甲说：我是第一名，乙说：我是第一名，丙说:乙是第一名。丁说：我不是第一名，若这四人中只有一个人说的是真话且获得第一名的只有一人，则第一名的是（ ‎ A.甲 B.乙 C. 丙 D. 丁 ‎ A.2 B. 3 C . 4 D. 5 ‎ ‎10、在长方体中，，，则异面直线与所成角的余弦值为 A． B． C． D．‎ ‎11．已知，是椭圆的左，右焦点，是的左顶点，点在过且斜率为的直线上，为等腰三角形，，则的离心率为 A． ‎ B． C． D．‎ 12、 已知定义在上的函数满足：函数的图像关于直线对称，且当时，.若，则a,b,c的大小关系是（ ）‎ A. a>b>c B. b>a>c C. c>a>b D.a>c>b 一、 填空题：‎ ‎15.A,B,C,D均在同一个球上，且AB,AC,AD两两互相垂直，且AB=1,AC=2,AD=3，则该球的表面积为 ‎ .‎ ‎16．已知点和抛物线，过的焦点且斜率为的直线与交于，两点．若，则________．‎ 二、 解答题：‎ 17. 在数列中，，且 （1） 证明：数列是等差数列；‎ （2） 求数列的前项和。‎ ‎18、如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.‎ ‎（Ⅰ）证明：PB∥平面AEC；‎ ‎（Ⅱ）设PC与平面ABCD所成的角的正弦为，AP=1，AD=，求三棱锥E-ACD的体积.‎ ‎19.某高中有高一新生500名，分成水平相同的两类教学实验，为对比教学效果，现用分层抽样的方法从两类学生中分别抽取了40人，60人进行测试.‎ ‎（1）求该学校高一新生两类学生各多少人？‎ ‎（2）经过测试，得到以下三个数据图表：‎ 图1：75分以上两类参加测试学生成绩的茎叶图 图2：100名测试学生成绩的频率分布直方图 下图表格：100名学生成绩分布表：‎ ‎①先填写频率分布表中的六个空格，然后将频率分布直方图（图2）补充完整；‎ ‎②该学校拟定从参加考试的79分以上（含79分）的类学生中随机抽取2人代表学校参加市比赛，求抽到的2人分数都在80分以上的概率.‎ 20. 椭圆的左、右焦点分别为，右顶点为A，上顶点为B，且满足向量 ‎ （1） 若，求椭圆的标准方程;‎ （2） 设为椭圆上异于顶点的点，以线段PB为直径的圆经过F1，问是否存在过F2的直线与该圆相切？若存在，求出其斜率；若不存在，说明理由。‎ 21. 设函数。‎ （1） 若是的极值点，求的值。‎ （2） 已知函数，若在区间（0,1）内有零点，求的取值范围。‎ ‎22.[选修4—5：参数方程选讲]（10分）在直角坐标系中，曲线的参数方程是 ‎（t是参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程是 （1） 求曲线的普通方程和曲线的直角坐标方程；‎ （2） 若两曲线交点为A、B，求 ‎23．[选修4—5：不等式选讲]（10分）‎ 设函数．‎ ‎⑴画出的图像；‎ ‎⑵当， ，求的最小值．‎ 文科数学答案 一、选择题：1----5ACBDA,6-------10CBCAD 11-----12DB 二、 填空题：13. 14. 15. 16.2‎ 三、 解答题：‎ ‎17.解析：（1）的两边同除以，得 ‎，又，..............4分 所以数列是首项为4，公差为2的等差数列.............6分 ‎(2)由（1）得，即,...........8分 故................10‎ 所以=..........12分 ‎18.答案：(1)连接BD交AC于点F，连接EF 则在三角形BDP中，点E是PD的中点，点F是BD的中点，即线段EF是的中位线 所以‖EF，又因为平面AEC，平面AEC，所以‖平面AEC......6‎ (2) 所以，所以 所以........12分 ‎19解：（1）由题意知A类学生有（人）则B类学生有500－200=300（人）. …2分 ‎（2）①表一 ‎…………………5分 图二 组号 分组 频数 频率 ‎1‎ ‎5‎ ‎0.05‎ ‎2‎ ‎20‎ ‎0.20‎ ‎3‎ ‎25‎ ‎0.25‎ ‎4‎ ‎35‎ ‎0.35‎ ‎5‎ ‎10‎ ‎0.10‎ ‎6‎ ‎5‎ ‎0.05‎ 合计 ‎100‎ ‎1.00‎ ‎…………………8分 ‎②79分以上的B类学生共4人，记80分以上的三人分别是，79分的学生为.‎ 从中抽取2人，有（12）、（13）、（1a）、（23）、（2a）、（3a）共6种抽法；‎ 抽出2人均在80分以上有：（12）、（13）、（23）共3种抽法 则抽到2人均在80分以上的概率为…………………12分 20、 解析：（1）易知，因为 所以为等腰三角形 所以b=c，由可知 故椭圆的标准方程为：.............5分 ‎（2）由已知得 设椭圆的标准方程为，的坐标为..........7分 因为,所以 由题意得,所以 又因为P在椭圆上，所以,由以上两式可得 因为P不是椭圆的顶点，所以，故 设圆心为，则 圆的半径.........9分 假设存在过的直线满足题设条件，并设该直线的方程为 由相切可知,所以 即，解得...........12 分 故存在满足条件的直线。‎ 20. 解析：（1），，‎ 因为是的极值点，所以，解得..........5分 ‎(2)，‎ ‎。‎ ‎①当时，‎ 恒成立，单调递减，又 因此函数在区间内没有零点。‎ ‎②当时，单调递增 时，单调递减 又，因此要使函数在区间内有零点，必有，‎ 所以 解得，舍去 ‎③当时，，，单调递减 又，因此要使函数在区间内有零点，必有，‎ 解得满足条件 综上可得，的取值范围是（-）.............12‎ 22. 解：（1）曲线的普通方程是:‎ 曲线的直角坐标方程是：.............5分 ‎(2)因为是过点（）的直线 所以的参数方程为： （为参数）‎ 代入的普通方程，得 解得，故...........10分 ‎23．（1）的图像如图所示．‎ ‎.......5‎ ‎（2）由（1）知，的图像与轴交点的纵坐标为，且各部分所在直线斜率的最大值为，故当且仅当且时，在成立，因此的最小值为．........10‎