2013新课标全国卷Ⅱ(文)数学试题
2013·新课标全国卷Ⅱ(文科数学)
1. 已知集合M={x|-3
b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( )
A. B.
C. D.
5.D [解析] 设PF2=x, 则PF1=2x,由椭圆定义得3x=2a,结合图形知,=⇒=,故选D.
6. 已知sin 2α=,则cos2=( )
A. B.
C. D.
6.A [解析] cos2===,故选A.
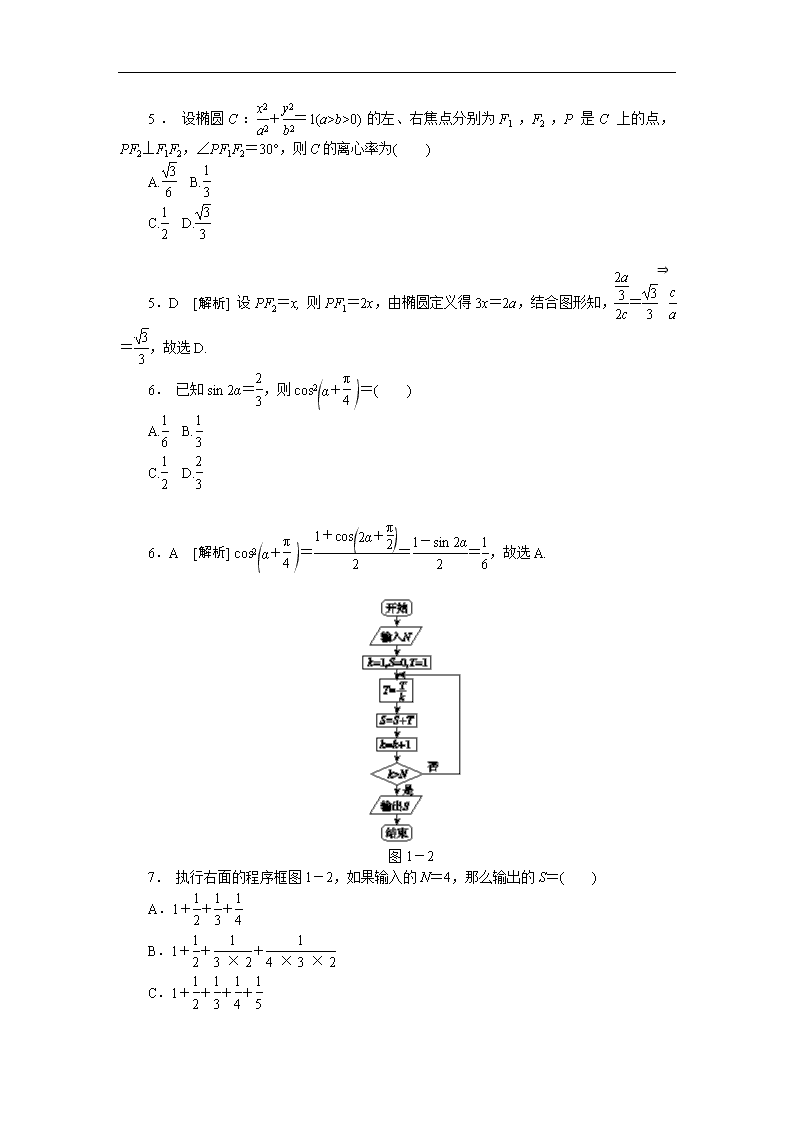
图1-2
7. 执行右面的程序框图1-2,如果输入的N=4,那么输出的S=( )
A.1+++
B.1+++
C.1++++
D.1++++
7.B [解析] k=1,T=1,S=1;k=2,T=,S=1+;k=3,T=,S=1++;k=4,T=,S=1+++,k=5>4成立,输出S,答案为B.
8., 设a=log32,b=log52,c=log23,则( )
A.a>c>b B.b>c>a
C.c>b>a D.c>a>b
8.D [解析] a-b=log32-log52=-=>0⇒a>b,c=log23>1,a<1,b<1,所以c>a>b,答案为D.
9. 一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为( )
图1-3
9.A [解析] 在空间直角坐标系O-xyz中画出三棱锥,由已知可知三棱锥O-ABC为题中所描叙的四面体,而其在zOx平面上的投影为正方形EBDO,故选A.
图1-4
10. 设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为( )
A.y=x-1或y=-x+1
B.y=(x-1)或y=-(x-1)
C.y=(x-1)或y=-(x-1)
D.y=(x-1)或y=-(x-1)
10.C [解析] 抛物线的焦点为F(1,0),若A在第一象限,如图1-5,设AF=3m,BF=m.过B作AD的垂线交AD于G,则AG=2m,由于AB=4m,故BG=2m,tan∠GAB=.∴直线AB的斜率为.同理,若A在第四象限,直线AB的斜率为-,故答案为C.
图1-5
11.,,, 已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
A.∃x0∈,f(x0)=0
B.函数y=f(x)的图像是中心对称图形
C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)单调递减
D.若x0是f(x)的极值点,则f′(x0)=0
11.C [解析] x→-∞时,f(x)<0,x→+∞时,f(x)>0,又f(x)连续,∃x0∈,f(x0)=0,A正确.通过平移变换,函数可以化为f(x)=x3+c,从而函数y=f(x)的图像是中心对称图形,B正确.若x0是f(x)的极小值点,可能还有极大值点x1,若x1x-成立,即a>.由于x-是(0,+∞)上的增函数,故x->0-=-1,所以a>-1.答案为D.
13. 从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是________.
13.0.2 [解析] 任取两个数有10种取法,和为5的取法有2种,故概率为=0.2.
14., 已知正方形ABCD的边长为2,E为CD中点,则·=________.
14.2 [解析] 如图建立平面直角坐标系,则
=(1,2),=(-2,2),所以·=2.
图1-6
15. 已知正四棱锥O-ABCD的体积为,底面边长为,则以O为球心,OA为半径的球的表面积为________.
15.24π [解析] 设O到底面的距离为h,则×3×h=⇒h=,OA==,故球的表面积为4π×()2=24π.
16. 函数y=cos(2x+φ)(-π≤φ<π)的图像向右平移个单位后,与函数y=sin的图像重合,则φ=________.
16. [解析] 由已知,y=cos(2x+φ)的图像向右平移得到y=cos(2x-π+φ)=-cos(2x+φ).y=sin=-cos=-cos,两个函数图像重合,故φ=π.
17., 已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
17.解:(1)设{an}的公差为d.由题意,a=a1a13,
即(a1+10d)2=a1(a1+12d),
于是d(2a1+25d)=0.
又a1=25,所以d=0(舍去),d=-2.
故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.从而
Sn=(a1+a3n-2)
=(-6n+56)
=-3n2+28n.
18.,, 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2,求三棱锥C-A1DE的体积.
图1-7
18.解:(1)证明:联结AC1交A1C于点F,则F为AC1中点.又D是AB中点,联结DF,则BC1∥DF.因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.
图1-8
(2)因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2 得∠ACB=90°,CD=,A1D=,DE=,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以VC-A1DE=××××=1.
图1-9
19., 经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图1-9所示.经销商为下一个销售季度购进了130 t该产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率.
19.解:(1)当X∈[100,130)时,
T=500X-300(130-X)
=800X-39 000.
当X∈[130,150]时,T=500×130=65 000.
所以T=
(2)由(1)知利润T不少于57 000元当且仅当
120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
20., 在平面直角坐标系xOy中,已知圆P在x轴上截得线段长为2 ,在y轴上截得线段长为2 .
(1)求圆心P的轨迹方程;
(2)若P点到直线y=x的距离为,求圆P的方程.
20.解:(1)设P(x,y),圆P的半径为r.
由题设y2+2=r2,x2+3=r2.从而y2+2=x2+3.
故P点的轨迹方程为y2-x2=1.
(2)设P(x0,y0),由已知得
=.
又P点在双曲线y2-x2=1上,从而得
由得
此时,圆P的半径r=.
由得
此时,圆P的半径r=.
故圆P的方程为x2+(y-1)2=3或x2+(y+1)2=3.
21., 已知函数f(x)=x2e-x.
(1)求f(x)的极小值和极大值;
(2)当曲线y=f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围.
21.解:(1)f(x)的定义域为(-∞,+∞).
f′(x)=-e-xx(x-2).①
当x∈(-∞,0)或x∈(2,+∞)时,f′(x)<0;
当x∈(0,2)时,f′(x)>0.
所以f(x)在(-∞,0),(2,+∞)单调递减,在(0,2)单调递增.
故当x=0时,f(x)取得极小值,极小值为f(0)=0;当x=2时,f(x)取得极大值,极大值为f(2)=4e-2.
(2)设切点为(t,f(t)),则l的方程为
y=f′(t)(x-t)+f(t).
所以l在x轴上的截距为
m(t)=t-=t+=t-2++3.
由已知和①得t∈(-∞,0)∪(2,+∞).
令h(x)=x+(x≠0),则当x∈(0,+∞)时,h(x)的取值范围为[2 ,+∞);当x∈(-∞,-2)时,h(x)的取值范围是(-∞,-3).
所以当t∈(-∞,0)∪(2,+∞)时,m(t)的取值范围是(-∞,0)∪[2 +3,+∞).
综上,l在x轴上的截距的取值范围是(-∞,0)∪[2 +3,+∞).
22. 选修4-1:几何证明选讲
如图1-10,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
图1-10
22.解:(1)因为CD为△ABC外接圆的切线,所以∠DCB=∠A,由题设知=,故△CDB∽△AEF,所以∠DBC=∠EFA.
因为B,E,F,C四点共圆,所以∠CFE=∠DBC,故∠EFA=∠CFE=90°.
所以∠CBA=90°,因此CA是△ABC外接圆的直径.
图1-11
(2)联结CE,因为∠CBE=90°,
所以过B,E,F,C四点的圆的直径为CE,
由DB=BE,有CE=DC.
又BC2=DB·BA=2DB2,
所以CA2=4DB2+BC2=6DB2.
而DC2=DB·DA=3DB2,
故过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为.
23. 选修4-4:坐标系与参数方程
已知动点P,Q都在曲线C:(t为参数)上,对应参数分别为t=α与t=2α(0<α<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.
23.解:(1)依题意有P(2cos α,2sin α),Q(2cos 2α ,2sin 2α),因此M(cos α+cos 2α,sin α+sin 2α).
M的轨迹的参数方程为(α为参数,0<α<2π).
(2)M点到坐标原点的距离
d==(0<α<2π).
当α=π时,d=0,故M的轨迹过坐标原点.
24. 选修4-5:不等式选讲
设a,b,c均为正数,a+b+c=1.
证明:(1)ab+bc+ca≤;
(2)++≥1.
24.证明:(1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca得a2+b2+c2≥ab+bc+ca.
由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤.
(2)因为+b≥2a,+c≥2b,+a≥2c,
故+++(a+b+c)≥2(a+b+c),
即++≥a+b+c.
所以++≥1.