- 2021-05-28 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
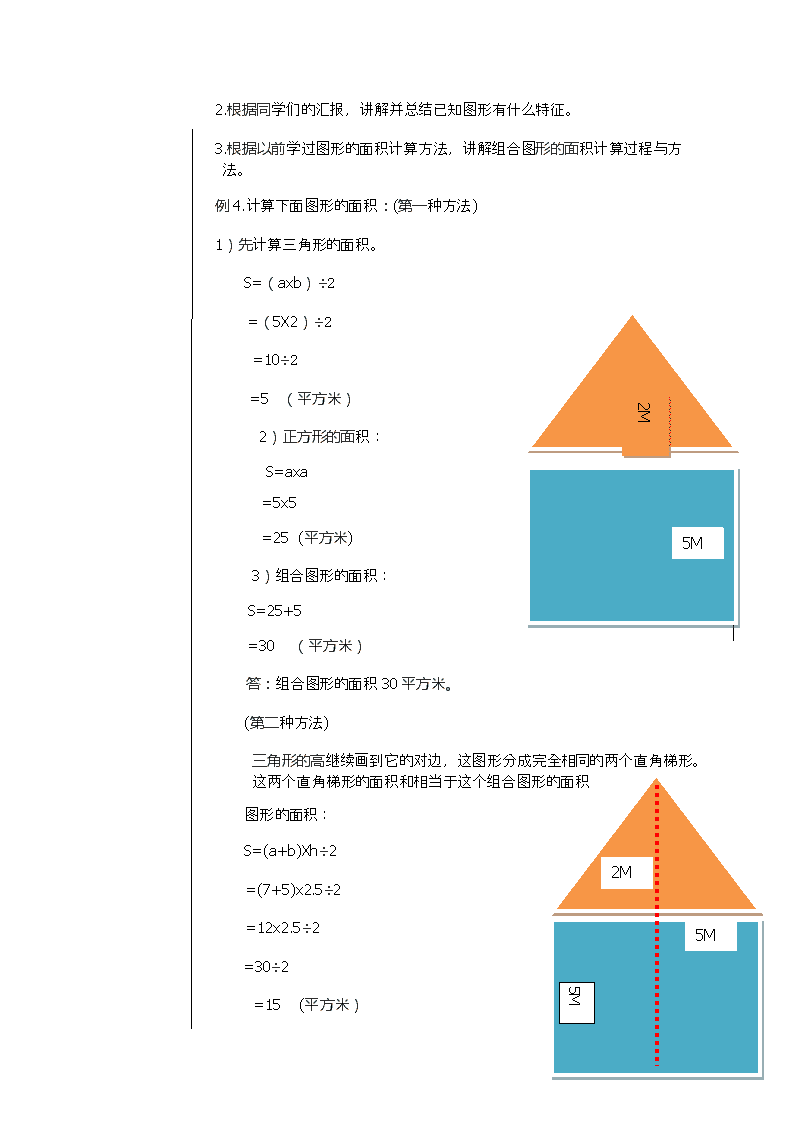
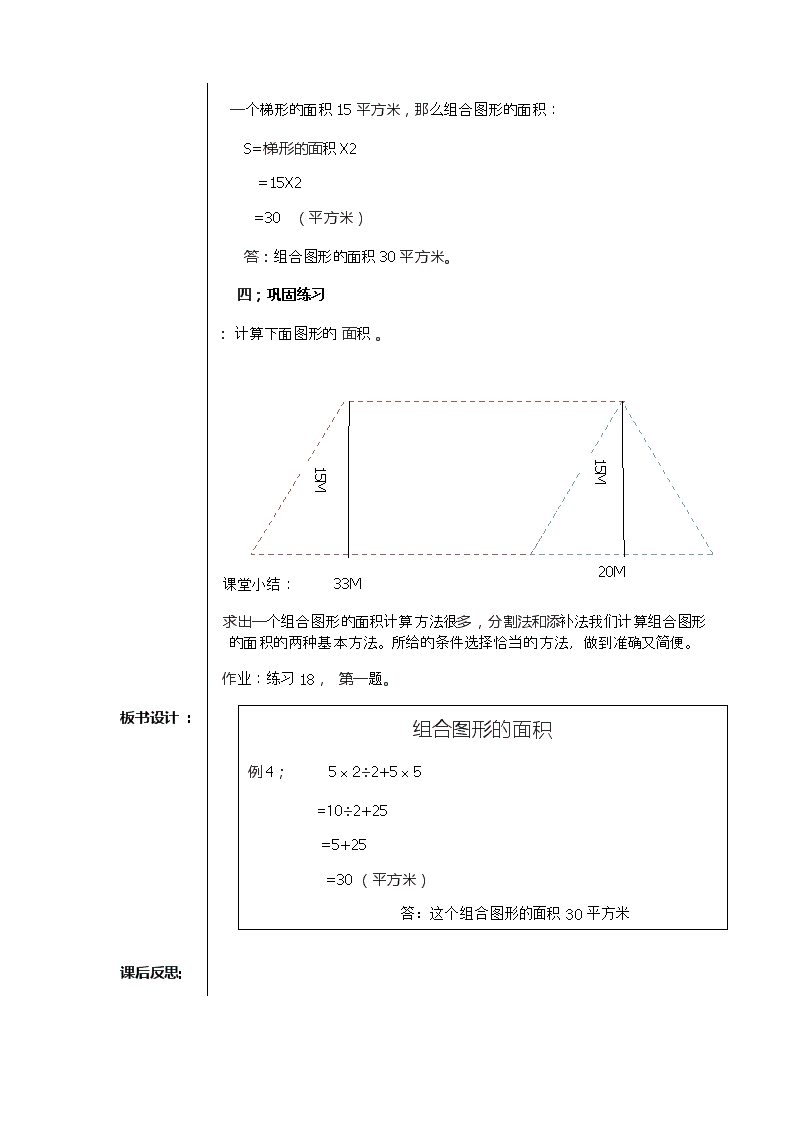
五年级上册数学教案-5 组合图形的面积 ︳青岛版 (2)
组合图形的面积 课题 : 组合图形的面积 教学内容 : 教学例4. 教学时间 ; 教学目标: 1.知识与技能 在自主探索活动中,理解计算组合图形面积的多方法,掌握用分解法求组合图形的面积。 2.过程与方法 能根据各种组合图形的条件,有效地选择计算方法并进行正确解答。 3.情感态度与价值观 提高学生运用新知识解决实际问题能力,在自主探索中培养他们的创新精神。 教学重点 : 在自主探索活动中,理解计算组合图形面积的多种解法,掌握用分解法求组合图形的面积。 教学难点 : 用恰当的方法,能准确求出组合图形的面积。 教法 : 讲解法,启示法,练习法。 学法 : 合作学习,自主学习。 课型 : 新授课 课程资源 : 直尺,课件。 教学过程 : 一;前提测评: 同学们我们学过了那些图形的面积计算?谁来说一说?谁能上黑板画一画? 二;导入新课: 问这道题并总结而导入新课。 三;新课内容: 1.让学生观察书上的插图并板书课题。 2.根据同学们的汇报,讲解并总结已知图形有什么特征。 3.根据以前学过图形的面积计算方法,讲解组合图形的面积计算过程与方法。 例4.计算下面图形的面积:(第一种方法) 1)先计算三角形的面积。 S=(axb)÷2 =(5X2)÷2 =10÷2 2M =5 (平方米) 2)正方形的面积: 5M S=axa =5x5 5M =25 (平方米) 3)组合图形的面积: S=25+5 =30 (平方米) 答:组合图形的面积30平方米。 (第二种方法) 5M 2M 5M 三角形的高继续画到它的对边,这图形分成完全相同的两个直角梯形。这两个直角梯形的面积和相当于这个组合图形的面积 图形的面积: S=(a+b)Xh÷2 =(7+5)x2.5÷2 =12x2.5÷2 =30÷2 =15 (平方米) 一个梯形的面积15平方米,那么组合图形的面积: S=梯形的面积X2 =15X2 =30 (平方米) 答:组合图形的面积30平方米。 四;巩固练习 : 计算下面图形的 面积 。 15M 15M 20M 33M 课堂小结: 求出一个组合图形的面积计算方法很多,分割法和添补法我们计算组合图形的面积的两种基本方法。所给的条件选择恰当的方法,做到准确又简便。 作业:练习18, 第一题。 组合图形的面积 例4; 5ⅹ2÷2+5ⅹ5 =10÷2+25 =5+25 =30 (平方米) 答:这个组合图形的面积30平方米 板书设计 : 课后反思: 课题:组合图形的面积 班级: 学号: 查看更多