华师版九年级上册数学同步练习课件-第23章 图形的相似-23相似三角形的应用(第五课时)

华师版九年级上册数学同步练习课件-第23章 图形的相似-23相似三角形的应用(第五课时)

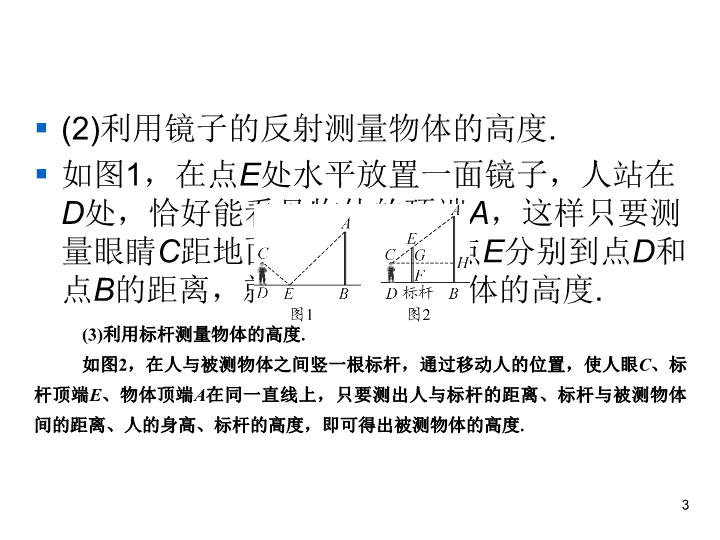
第23章　图形的相似 23.3　相似三角形 4　相似三角形的应用(第五课时) § 知识点1　测量物体的高度 § 利用相似三角形的有关性质可以计算那些不 能直接测量的物体的高度. § (1)利用阳光下的影子测量物体的高度. § 测量同一时刻物体的影长L和自己(或标杆)的 影长l，再结合自己的身高，就能得出物体的 高度. 2 § (2)利用镜子的反射测量物体的高度. § 如图1，在点E处水平放置一面镜子，人站在 D处，恰好能看见物体的顶端A，这样只要测 量眼睛C距地面的高度CD及点E分别到点D和 点B的距离，就能得出被测物体的高度. 3 (3)利用标杆测量物体的高度. 如图2，在人与被测物体之间竖一根标杆，通过移动人的位置，使人眼C、标 杆顶端E、物体顶端A在同一直线上，只要测出人与标杆的距离、标杆与被测物体 间的距离、人的身高、标杆的高度，即可得出被测物体的高度. § 答案：4.4 4 § 知识点2　测量不能到达的两点间的距离 § 方法：通过测量便于测量的线段，利用三角 形相似对应边成比例，可求得不能到达的两 点间的距离. § 原理：常常构造“A”型或“X”型相似三角 形，为了使问题简便，尽量构造直角三角形. 5 § 【典例2】如图，要测量的A、B两点被池塘隔开，小李在AB外任 选一点C，连结CA、CB，分别在CA、CB上取点E、F，使 EF∥AB且CE＝AE，量得E、F两点间的距离等于12.5米，则A、 B两点间的距离是________米. 6 § 答案：25 7 § 1．【2018·山东临沂中考】如图，利用标杆BE测量建筑物的高 度.已知标杆BE高1.2 m，测得AB＝1.6 m，BC＝12.4 m，则建筑 物CD的高是 (　　) § A．9.3 m　 § B．10.5 m　 § C．12.4 m　 § D．14 m 8 B　 § 2．如图，小明用自制的直角三角形纸板DEF 测量树AB的高度，测量时，使直角边DF保 持水平状态，其延长线交AB于点G；使斜边 DE所在的直线经过点A．测得边DF离地面的 高度为1 m，点D到AB的距离等于7.5 m.已知 DF＝1.5 m，EF＝ 0.6 m，那么树AB的高 度等于 (　　) § A．4 m　 § B．4.5 m　 § C．4.6 m　 § D．4.8 m 9 A　 § 3．如图，为了估计河的宽度，在河的对岸选 定一个目标点P，在近岸取点Q和S，使点P、 Q、S在一条直线上，且直线PS与河岸垂直， 在过点S且与PS垂直的直线a上选择适当的点 T，连结PT，PT过点Q且与PS垂直的直线b 的交点为R.如果QS＝ 60 m，ST＝120 m， QR＝80 m，则河的宽度PQ为 (　　) § A．40 m　 § B．60 m　 § C．120 m　 § D．180 m 10 C　 § 4．【四川绵阳中考】为测量操场上旗杆的高 度，小丽同学想到了物理学中平面镜成像的 原理.她拿出随身携带的镜子和卷尺，先将镜 子放在脚下的地面上，然后后退，直到她站 直身子刚好能从镜子里看到旗杆的顶端E， 标记好脚掌中心位置为B，测得脚掌中心位 置B到镜面中心C的距离是50 cm，镜面中心 C距离旗杆底部D的距离为4 m，如图所示.已 知小丽同学的身高是1.54 m，眼睛位置A距 离小丽头顶的距离是4 cm，则旗杆DE的高度 等于 (　　) § A．10 m　 § B．12 m　 § C．12.4 m　 § D．12.32 m 11 B　 § 5．如图，小军、小珠之间的距离为2.7 m，他们在同一盏路灯下的影长 分别为1.8 m、1.5 m，已知小军、小珠的身高分别为1.8 m、1.5 m，则 路灯的高为_____ m. 12 3　 13 § 6．如图，身高为1.8米的某学生想测量学校 旗杆的高度，当他站在B处时，他头顶端的 影子正好与旗杆顶端的影子重合，并测得AB ＝2米，BC＝18米，则旗杆CD的高度是 ______米. 14 18　 § 7．【2018·吉林中考】如图是测量河宽的示意图，AE与BC相交于点D， ∠B＝∠C＝90°，测得BD＝120 m，DC＝60 m，EC＝50 m，求得河 宽AB＝_______m. 15 100　 § 8．兴趣小组的同学要测量树的高度.在阳光 下，一名同学测得一根长为1米的竹竿的影长 为0.4米，同时另一名同学测量树的高度时， 发现树的影子不全落在地面上，有一部分落 在教学楼的第一级台阶上，测得此影子长为 0.2米，一级台阶高为0.3米，如图所示，若 此时落在地面上的影长为4.4米，则树高为 __________. 16 11.8米　 17 § 9．如图，在△ABC中，AB＝AC，BD＝CD， CE⊥AB于点E.求证：BD·BC＝BE·BA． 18 § 10．一块材料的形状是锐角△ABC，边BC＝ 120 mm，高AD＝80 mm，把它加工成正方 形零件如图所示，使正方形的一边在BC上， 其余两个顶点分别在AB、AC上. § (1)求证：△AEF∽△ABC； § (2)求这个正方形零件的边长. 19 20