- 2021-05-28 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三年级数学下册课件-2整理和复习人教版 (2)
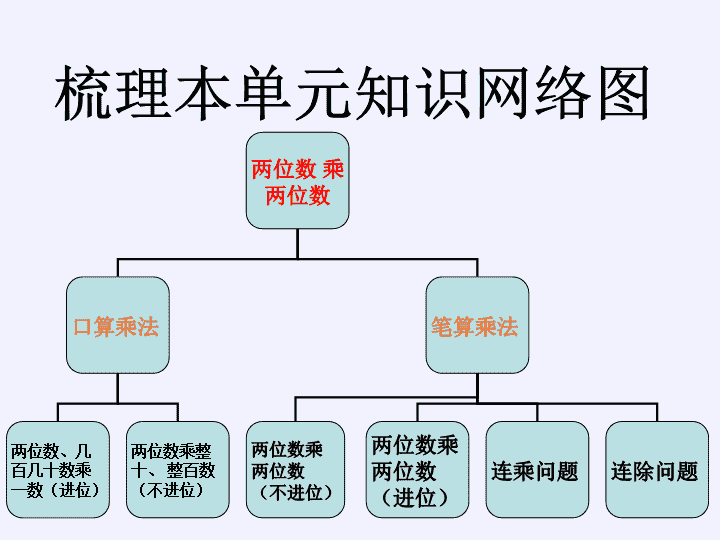
整理和复习 两位数 乘 两位数 口算乘法 笔算乘法 两位数、几 百几十数乘 一数(进位 ) 两位数乘整 十、 整百数 (不进位) 两位数乘 两位数 (不进位 ) 两位数乘 两位数 (进位) 连乘问题 连除问题 梳理本单元知识网络图 观察表格,小组 讨论: 哪些积是口算 得到的?是怎样 口算的? 440 460 480 500 520 540 560 580 600 650 660 690 720 750 780 810 840 870 900 1050 1200 1160 1120 1080 1040 1000 960 920 880 1350 1100 1150 1200 1250 1300 1350 1400 1450 1500 1650 1320 1380 1440 1500 1560 1620 1680 1740 1800 观察表格,小组 讨论: 哪些积是口算 得到的?是怎样 口算的? 40×4= 120×30= 16 0 36 00 口算两位数乘整十、整百数: 先把两个因数0前面的数字相乘,再 看两个因数一共有几个0,就在乘积的 末尾添上几个0。 440 460 480 500 520 540 560 580 600 650 660 690 720 750 780 810 840 870 900 1050 1200 1160 1120 1080 1040 1000 960 920 880 1350 1100 1150 1200 1250 1300 1350 1400 1450 1500 1650 1320 1380 1440 1500 1560 1620 1680 1740 1800 观察表格,小组 讨论: 哪些积是笔算 得到的?是怎样 笔算的? 梳理笔算方法 1 5 6 6 × 2 9 5 4 6 8 4 8 1 0 3 两位数乘两位数的计算方 法: ①先用第二个因数个位上 的数去乘第一个因数,得 数的末尾和因数的个位对 齐; ②再用第二个因数十位上 的数去乘第一个因数,得 数的末尾和因数的十位对 齐; ③然后将两次乘得的数相 加。 下面的计算正确吗?把错误的改正过来。 √ ( )( ) 2 3 6 2 2 5 9 81 1 8 1 1 6 9 4 × 3 4 2 1 46 × ×× 8 1 1 1 2 9 8 3 6 7 1 4 √ 68 注意: 笔算时,要注意 每次乘得的数的 末位应该和哪一 位对齐,还要注 意记住进位数, 正确处理进位问 题。 (1)今年冬冬家一共收获橘子多少千 克? 冬冬家有4行橘子树,每行8棵,今年 平均每棵收获橘子25千克。 梳理解决问题的方法 : (1)今年冬冬家一共收获橘子多少千 克? 8×4=32(棵) 32×25=800(千克) 答:今年冬冬家一共收获橘子800千克。 冬冬家有4行橘子树,每行8棵,今年 平均每棵收获橘子25千克。 梳理解决问题的方法 : 25×8=200(千克)200×4=800(千克 ) 答:今年冬冬家一共收获橘子800千克。 (2)把这些橘子装箱,每箱8千克。 用5辆三轮车运走,平均每车运多少箱? 冬冬家有4行橘子树,每行8棵,今年 平均每棵收获橘子25千克。 梳理解决问题的方法 : (2)把这些橘子装箱,每箱8千克。 用5辆三轮车运走,平均每车运多少箱? 800÷5=160(千克)160÷8=20(箱) 答:平均每车运20箱。 冬冬家有4行橘子树,每行8棵,今年 平均每棵收获橘子25千克。 梳理解决问题的方法 : 800÷8=100(箱) 100÷5=20(箱) 答:平均每车运20箱。 (1)今年冬冬家一共收获橘子多少千 克? (2)把这些橘子装箱,每箱8千克。用 5辆三轮车运走,平均每车运多少箱? (3)如果每千克橘子卖2元钱。你能提 出数学问题并解答吗? 冬冬家有4行橘子树,每行8棵,今年 平均每棵收获橘子25千克。 梳理解决问题的方法 : 我们既可以从已知信息出发,边读边想: 这两个信息可以求出什么?与其他信息 有什么关系?能求出什么?我们也可以 从问题出发进行分析:要求出这个问题 需要知道哪些信息?所需要的信息题目 中能直接找到吗?如果没有可以通过哪 些信息求出来?其实很多问题都可以用 这两种方法进行分析,它们能够帮助我 们很快找到解决问题的途径。 我们既可以从已知信息出发,边读边想: 这两个信息可以求出什么?与其他信息 有什么关系?能求出什么?我们也可以 从问题出发进行分析:要求出这个问题 需要知道哪些信息?所需要的信息题目 中能直接找到吗?如果没有可以通过哪 些信息求出来?其实很多问题都可以用 这两种方法进行分析,它们能够帮助我 们很快找到解决问题的途径。 我们既可以从已知信息出发,边读边想: 这两个信息可以求出什么?与其他信息 有什么关系?能求出什么?我们也可以 从问题出发进行分析:要求出这个问题 需要知道哪些信息?所需要的信息题目 中能直接找到吗?如果没有可以通过哪 些信息求出来?其实很多问题都可以用 这两种方法进行分析,它们能够帮助我 们很快找到解决问题的途径。 一、看谁算的又对又快。 30×23= 13×20= 24×5= 100×70= 22×40= 60×70= 31 ×3= 14×50= 17×400= 690 260 7000 4200 93 6800 120 880 700 二、辨是非,对的打“√ ”,错 的打“×”。 1.两位数乘两位数,积不 是四位数,就是三位数。 ( ) 2.12×4的积与16×3的积 相等。( ) 3.两个数相乘,乘数末尾 没有0,积的末尾也没有0。 ( ) √ √ × 三、将正确答案的字母填在 括号里。 1.3个蛋糕装一袋,6袋蛋糕装一 盒,36盒有多少个蛋糕?下面算式 正确的是( )。 A.36÷(6×3) B.36÷6÷3 C .36×6×3 2.将240本书分给2各班,每个班 有4个小组,平均每个小组多少本书? 下面算式错误的是( )。 A.240÷2÷4 B.240÷(2×4) C .2×4×240 C C 四、比较每组算式得数的大小,你 发现了什么? (1)30 × 30 = (2)50 × 50 = 31 × 29 = 51 × 49 = 32 × 28 = 52 × 48 = 33 × 27 = 53 × 47 = 发现: 900 899 896 891 2500 2499 2496 2491 在乘法中,当两个因数的和不变时,这 两个因数的差越小,它们的积越大。 两位数 乘 两位数 口算乘法 笔算乘法 两位数、几 百几十数乘 一数(进位 ) 两位数乘整 十、 整百数 (不进位) 两位数乘 两位数 (不进位 ) 两位数乘 两位数 (进位) 连乘问题 连除问题 梳理本单元知识网络图 谢 谢查看更多