九年级数学上册第二十二章二次函数22-1二次函数的图象和性质3y=a(x-h)2+k教学课件新版 人教版

九年级数学上册第二十二章二次函数22-1二次函数的图象和性质3y=a(x-h)2+k教学课件新版 人教版

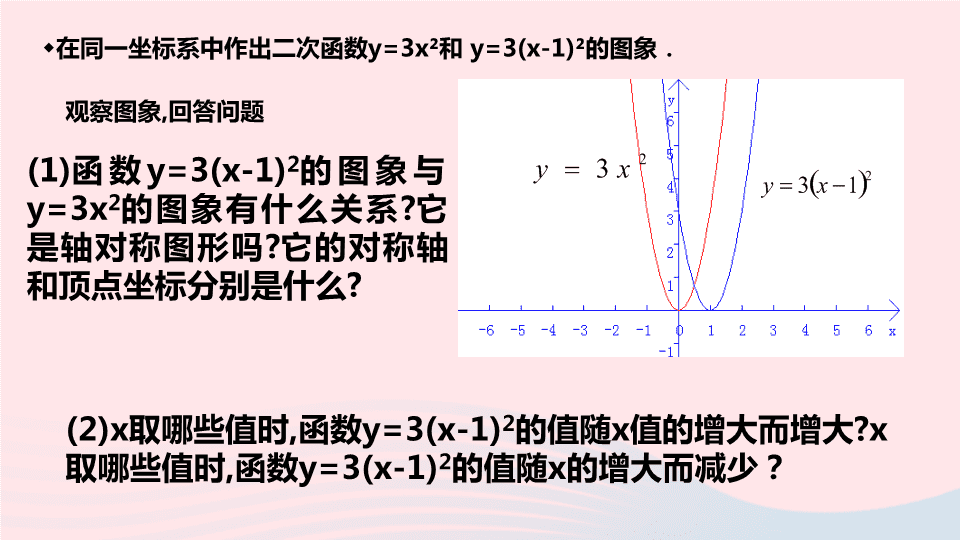
第 22 章：二次函数 22.1 二次函数的图像和性质 22.1.3 y=a(x-h)²+k 学习目标： 1.经历探索二次函数y=a(x-h)²+k 的图象及性质的过程，了解y=a(x-h)²+k与y=ax²、 y=ax²+k、 y=a(x-h)²的图象之间的关系。 2.会用描点法画出二次函数y=a(x-h)²+k 的图象，熟练掌握二次函数y=a(x-h)²+k 的有关性质。 3.能够灵活运用二次函数y=a(x-h)²+k 的图象和性质解决有关问题。 观察图象 , 回答问题 (1) 函数 y=3(x-1) 2 的图象与 y=3x 2 的图象有什么关系 ? 它是轴对称图形吗 ? 它的对称轴和顶点坐标分别是什么 ? (2)x 取哪些值时 , 函数 y=3(x-1) 2 的值随 x 值的增大而增大 ?x 取哪些值时 , 函数 y=3(x-1) 2 的值随 x 的增大而减少？ 在同一坐标系中作出二次函数 y=3x² 和 y=3(x-1)² 的图象． 二次函数 y=-0.5x ² , y=-0.5(x+1) 2 和 y=-0.5(x+1) 2 -1 的图象有什么关系 ? 它们的开口方向 , 对称轴和顶点坐标分别是什么 ? 例 3 画出函数 y=-0.5 （ x+1 ） ²-1 的图像，指出它的开口方向、对称轴及顶点，抛物线 y=-0.5x² 经过怎样的变换可以得到抛物线 y=-0.5 （ x+1 ） ² -1 ？ 思考： 二次函数 y=-0.5(x+1) 2 -1 的 图象可以看作是抛物线 y=-0.5x 2 先沿着 x 轴向左平移 1 个单位 , 再沿直线 x=-1 向 上平移 1 个单位后得到的 . 二次函数 y=-0.5(x+1) 2 -1 的图象 和抛物线 y=-0.5x ² , y=-0.5(x+1) 2 有什么关系 ? 它的开口方向 , 对称轴和顶点坐标分别是什么 ? y=-½(x+1)² -1 y=-½x² y=-½(x+1)² 对称轴仍是平行于 y 轴的直线 (x=-1); 增减性与 y=-0.5x 2 类似 . 顶点是 (-1,-1) . 开口向下 , 当 x=-1 时 y 有 最大值 : 且 最大值是 -1. 先猜一猜 , 再 做一做 , 在同一坐标系中作二次函数 y=0.5(x+1) 2 -1, 会是什么样 ? 在同一坐标系中作出二次函数 y=-3(x-1) 2 +2 , y=-3(x-1) 2 -2,y=-3x ² 和 y=-3(x-1) 2 的图象 二次函数 y=-3(x-1) 2 +2 与 y=-3(x-1) 2 -2 和 y=-3x ² , y=-3(x-1) 2 的图象有什么关系 ? 它们是轴对称图形吗 ? 它的开口方向、对称轴和顶点坐标分别是什么 ? 当 x 取哪些值时， y 的值随 x 值的增大而增大 ? 当 x 取哪些值时， y 的值随 x 值的增大而减小 ? 对称轴仍是平行于 y 轴的直线 (x=1); 增减性与 y= -3x 2 类似 . 顶点分别是 (1,2) 和 (1,-2) . 二次函数 y=-3(x-1) 2 +2 与 y=-3(x-1) 2 +2 的图象可 以看作是抛物线 y=-3x 2 先沿着 x 轴向右平移 1 个 单位 , 再沿直线 x=1 向上 ( 或向下 ) 平移 2 个单位后 得到的 . 二次函数 y=-3(x-1) 2 +2 与 y=-3(x-1) 2 -2 的图象 和抛物线 y=-3x ² , y=-3(x-1) 2 有什么关系 ? 它的开口方向 , 对称轴和顶点坐标分别是什么 ? 当 x 取哪些值时， y 的值随 x 值的增大而增大 ? 当 x 取哪些值时， y 的值随 x 值的增大而减小 ? 开口向下 , 当 x=1 时 y 有 最大值 : 且 最大值 = 2 ( 或最大值 =-2). y X=1 与 y=-3x² 有关哟 一般地 , 由 y=ax² 的图象便可得到二次函数 y=a(x-h)²+k 的图象 : y=a(x-h)²+k(a≠0) 的图象可以看成 y=ax² 的图象先沿 x 轴整体左 ( 右 ) 平移 |h| 个单位 ( 当 h>0 时 , 向右平移 ; 当 h<0 时 , 向左平移 ), 再沿对称轴整体上 ( 下 ) 平移 |k| 个单位 ( 当 k>0 时向上平移 ; 当 k<0 时 , 向下平移 ) 得到的 . 因此 , 二次函数 y=a(x-h) ² +k 的图象是一条抛物线 , 它的开口方向、对称轴和顶点坐标与 a,h,k 的值有关 . 抛物线 y=a(x-h)²+k 有如下特点： （ 1 ）当 a ＞ 0 时，开口向上 ; 当 a ＜ 0 时，开口向下； （ 2 ）对称轴是直线 x=h ； （ 3 ）顶点坐标是 （ h ， k ） 。 二次函数 y=a(x-h) ² +k 与 y=ax² 的关系 二次函数 y=a(x-h) 2 +k 的图象和性质 １ . 顶点坐标与对称轴 ２ . 位置与开口方向 ３ . 增减性与最值 抛物线 顶点坐标 对称轴 位置 开口方向 增减性 最值 y=a(x-h) 2 +k (a>0) y=a(x-h) 2 +k (a<0) （ h ， k ） （ h ， k ） 直线 x=h 直线 x=h 由 h 和 k 的符号确定 由 h 和 k 的符号确定 向上 向下 当 x=-h 时 , 最小值为 k. 当 x=-h 时 , 最大值为 k. 在对称轴的左侧 ,y 随着 x 的增大而减小 . 在对称轴的右侧 , y 随着 x 的增大而增大 . 在对称轴的左侧 ,y 随着 x 的增大而增大 . 在对称轴的右侧 , y 随着 x 的增大而减小 . 根据图形填表： y x 例 4 要修建一个圆形喷水池，在池中心竖立安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线型柱在与池中心的水平距离为 1m 处达到最高，高度为 3m ，水管应多长？ 点（ 1 、 3 ）是顶点，知道 h=1 ， k=3 ，求出 a 就好啦 ! 点（ 3 、 0 ）在抛物线上，求 a 没问题。 解：如图建立直角坐标系，点（ 1 、 3 ）是顶点， 设抛物线的解析式为 Y=a （ x-1 ） ²+3 （ 0≤x≤3 ） 点（ 3 、 0 ）在抛物线上，所以有 0=a （ 3-1 ） ²+3 ∴ a=- ∴ y=- （ x-1 ） ²+3 （ 0≤x≤3 ） 当 x=0 时， y=2.25 ， 即 水管应长 2.25m 。 3 4 3 4 1. 指出下列函数图象的开口方向对称轴和顶点坐标及最值 : 　　　　 2.(1) 二次函数 y=3(x+1)2 的图象与二次函数 y=3x2 的图象有什么关系 ? 它是轴对称图形吗 ? 它的对称轴和顶点坐标分别是什么 ? （ 2 ）二次函数 y=-3(x-2)2 +4 的图象与二次函数 y=-3x 2 的图象有什么关系 ? ３．对于二次函数 y=3(x+1) 2 , 当 x 取哪些值时 ,y 的值随 x 值的增大而增大 ? 当 x 取哪些值时 ,y 的值随 x 值的增大而减小 ? 二次函数 y=3(x+1) 2 +4 呢 ? 4. 指出下列函数图象的开口方向 , 对称轴和顶点坐标 . 必要时作出草图进行验证 . 5. 填写下表 : y=a(x-h) ² +k 开口方向 对称轴 顶点坐标 a>0 向上 X=k （ h 、 k ） a<0 向下 X=k （ h 、 k ）