八年级数学上册第五章一次函数5-2一次函数复习课件苏教版

八年级数学上册第五章一次函数5-2一次函数复习课件苏教版

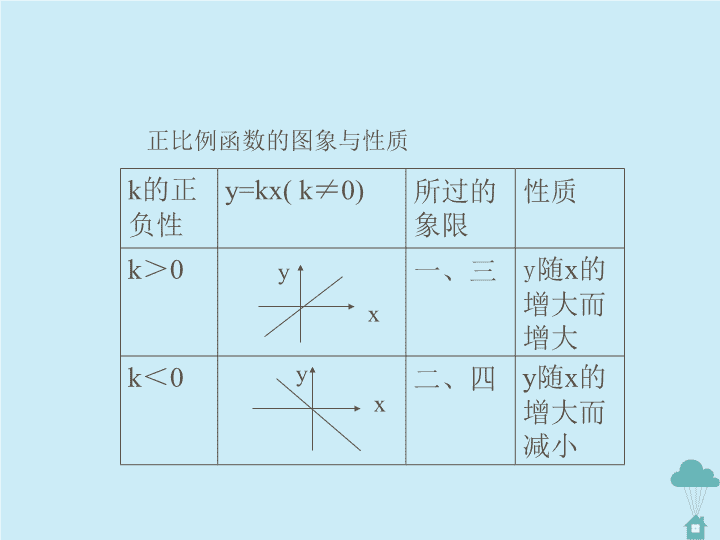
一次函数 1、一次函数的定义 一般地，如果y=kx+b（k、b是常数，k≠0），则y叫做x的 一次函数。特别地，当b=0时，y=kx(k≠0),这时 y叫做x的正 比例函数。 正比例函数y=kx(k≠0)的图象是过原点的一条直线。 正比例函数的图象与性质 k的正 负性 y=kx( k≠0) 所过的 象限 性质 k＞0 一、三 y随x的 增大而 增大 k＜0 二、四 y随x的 增大而 减小 x y x y 一次函数y=kx+b(k≠0)的图象与性质见下表(说明： k确定方向，b确定位置。 ) k、b的正 负 y=kx+b(k≠0)的 图象 所过象限 性质 k＞ 0 b＞0 一、二、 三 y随x的 增大而 增大 b＜0 一、三、 四 k＜ 0 b＞0 一、二、 四 y 随 x的 增大而 减小 b＜0 二、三、 四 x y xy x y xy 4.y=kx+b的图象与x轴交于点（-b/k,0)，与y轴交于点(0,b)。 5.关于y=kx+b的图象与坐标轴围成的三角形的面积。如图， 一次函数y=kx+b（k ≠ 0)于坐标轴交于A,B两点，则三角形 AOB的面积S＝[︱ -b/k︱ ×b]/2；或是已知三角形的面积， 可以求出在x轴与y轴上的截距，即是一次函数与两个坐标 轴的交点坐标，因此也可以求出函数解析式。 6、求两个一次函数的交点坐标的坐标，即是把两个一次函 数联列组成一个二元一次方程组，然后求出的方程组的解 即是两个一次函数的交点坐标。 A(0,b) B (-b/k,0) O x y 1、函数 y=kx+k与y=k/x(k≠0)在同一直角坐标系中的图象是 ( ) o x y A o x y B o x y C o x y D 范例: 已知y与 x+1成正比例，当x=5时，y=12，求y与x的函数关 系式 。 解：设y=k(x+1),由题意，当x=5时，y=12，即 12=k（5+1） 12=6 k k=2 故y=2(x+1) 已知y=y1+y2，y1与x成正比，y2与x成反比，并当x=1 时，y=-2，当x=2时y=-7，求y与x之间的函数关系式.。 解：设y1=k1x，y2=k2/x,则y=k1x+k2/x 由已知当x=1时，y=-2；x=2时，y=-7， 所以有 -2=k1+ k2 -7=2 k1+k2/2 解出k1=-4， k2=2 所以y=-4x+2/x 已知一个正比例函数和一个一次函数，它们的函数图象都过M（-2，1）， 且一次函数的图象与y轴交与Q（0，3）。 1） 求两个一次函数的解析式； 2） 在同一坐标系中画出两个一次函数的图象； 3） 设一次函数与x轴交与点P，求出三角形PQO的面积。 o 解：1）由已知可得一次函数经过了点P和点Q，正比例函数过了 点P，所以设正比例函数解析式为y=k1x，一次函数解析式为 y=k2x+b于是由1=-2k1，得k1=-1/2，故正比例函数解析式为y=-x/2； 而 1=-2k2+b b=3 解出k2=1，所以一次函数解析式为y=x+3 2）图象如右图 3）先求出P的坐标，即当y=0时，x=-3，所以P（-3，0）。三角 形PQO的面积S= │-3│× 3/2=9/2 y Q（0，3） x P y（元） 2 4 6 x 分 2 4 6 3.6 某市向北京打长途电话，设通话时间x(分)， 需付电话费y（元）。通话3分钟以内话费为 3.6元，请根据如图中y随x的变化图象，找出 通话5分钟，需付电话费为 元。 某天早晨，小强从家出发，以v1的速度前往学校，途中在 一家饮食店吃早点，之后，以v2的速度想学校行进。已知 v1＞v2，下面的图象中表示小强从家到学校的时间t（分） 与路程s（千米）之间的关系是( ) t(分钟） S（千米） t(分钟） t(分钟） t(分钟） S（千米） S（千米） S（千米） (A) (B) (C) (D) 某地区的水电资源丰富，并且得到了较好的开发，电力充足。某供电公司 为了鼓励居民用电，采用分段计费的方法计算电费。月用电量（度）与相 应的电费y（元）之间的函数关系的图象如图所示。 （1） 月用量为100度时，应交电费多少元？ （2） 当x≥100时，求y与 x之间的函数关系式。 （3） 用电量为260度时，应交电费多少元？ x(度） y(元） 60 110 100 2000 解（1）由图象可知，当月用量为100度时，应交电费60元； （2）当x≥100时，一次函数图象过了点（100，60）和（200， 110），于是设函数解析式为y=kx+b，代入两个点的坐标，有 60=100k+b 110=200k+b 解出k=1/2，b=10，所以解析式为y=x/2+10 （3）当x=260时，y=260/2+10=140 1、一根蜡烛长20cm，点燃后每小时燃烧4cm，燃烧过程中 蜡烛的高度ycm与燃烧时间x小时的函数关系用图象表示为 （ ） y(cm) x(小时）x(小时） y(cm)y(cm) y(cm) y(cm) x(小时） x(小时）5 10 10 20 20 20 20 10 10 10 5 5 510 10 10 (A) (B) (C) (D) x( 千克） 3 4 2 4 y(cm) 已知一挂重不超过10千克的弹簧，其长度y（cm）与挂重x（千 克）之间的函数关系如图所示，请根据图象回答下列问题（不 必写出过程） （1）( 1 ) y与x之间的函数关系式为 ； （2） 自变量x的取值范围为 ； （3） 弹簧本身的长度为 cm； ( 4 ) 当挂重为6千克时，弹簧的长度为 cm 。 1、某单位计划在新年期间组织员工到某地旅游，参加的人数估计在 10—25人，甲、乙两家旅行社的服务质量相同，且报价都是每人200 元。经过协商，甲旅行社表示可以给予每位七五折优惠；乙旅行社 表示可以免去一位的费用，其余的给予八折优惠。该单位选择哪家 旅行社支付的费用较少？ 解：该单位参加这次旅游的人数是x人，选择甲旅行社所需的费用为为y1元， 选择乙旅行社时所需的费用为y2元，则 y1=200× 0.75x，即y1=150x y2=200× 0.8（x-1），即y2=160x-160 讨论：1）若y1＞y2，得150x ＞160x-160,解得x＜16 2) 若y1＜y2，得150x＜160x-160,解得x＞16 3）若y1= y2，得150x=160x-160,解得x=16 因为参加的人数为10—25人，所以当x=16时，甲、乙两家收费相同；当 17≤x≤25时，选择甲旅行社费用较少；当10≤x≤15时，选择乙旅行社费用 较少。 练习 1、在函数y=2x+1，y=(3x-2)/5,y=x,y=2x/3,y=3x-5x2中，一次函数有 个 2、已知y+3与x-2成正比，且当x=1/2时，y=0，求当x=8时y的值。 3、如图，l甲、l乙分别是甲、乙两弹簧的长ycm与所挂物体质量 xkg之间的函数关系的图象。设甲每挂1kg的物体伸长的长度为k甲， 乙弹簧每挂1kg的物体伸长的长度为k乙， 则k甲与k乙的大小关系为 l乙 l甲 12 8 1 x(kg) 0 y(cm) 函数y=（m-1）x与反比例函数y=4m/x的图象大致 位置不可能的是（ ） o x y o A x y o B x y o C x y o D 某单位要制作一批宣传材料。甲公司提出：每份材料收费20元，另收3000元 的设计费；乙公司提出：每份材料收费30元，不收设计费。 （1） 什么情况下选择甲公司比较合算？ （2） 什么情况下选择乙公司比较合算？ （3） 什么情况下两家的收费相同？