- 2021-05-27 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件:17-1 勾股定理 (共17张PPT)_人教新课标
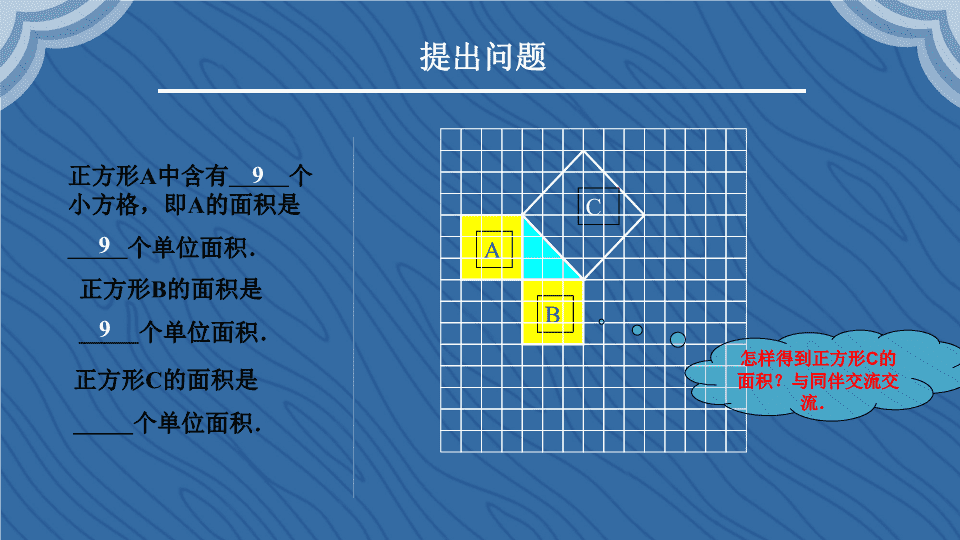
18.1勾股定理 提出问题 我们也来观察下图中的地 面,看看有什么发现? 毕达哥拉斯(公元前 572——前492年), 古希腊著名的哲学家、 数学家、天文学家。 概念:以等腰直角三角形两 直角边为边长的小正方形的面积 和, 等于以斜边为边长的正方形的面积。 即我们惊奇地发现等腰直角三角形的 三边之间有一种特殊的关系:斜边的 平方等于两直角边的平方和。 提出问题 A B C 正方形A中含有 个 小方格,即A的面积是 个单位面积. 正方形B的面积是 个单位面积. 正方形C的面积是 个单位面积. 9 9 9 怎样得到正方形C的 面积?与同伴交流交 流. 第一种方法:把C分割 成若干个直角边为整 数的三角形. C A B CS正方形 14 3 3 18 2 第二种方法:把C看成 边长为6的正方形面积 的一半. CS正方形 21 6 2 18 C A B 2.观察右边两个 图并填写下表: A B C 图1-2 A B C 图1-3 图1-3 图1-2 C的面积B的面积A的面积 16 9 25 4 9 13 A B C 图1-2 A B C 图1-3 3.三个正方形A,B, C面积之间有什么关系? SA+SB=SC 即:一个直角三角形两条直角 边上的正方形面积之和等于斜 边上的正方形的面积. A B C 图1-2 A B C 图1-3 4.你能发现直角三角形 三边长度之间存在什么关 系吗?与同伴交流. 面积关系:SA+SB=SC 2a 2b 2c=+三边关系: 5.分别以5厘米、12厘米 为直角边作出一个直角三 角形,并测量斜边的长 度.第4 题中的关系式对这 个三角形仍然成立吗? 语言表述:直角三角形两直角边的平方和等于斜边的平方. 归纳猜想命题 a b c 2 2 2a b c 理论证明:“赵爽弦图”的证法 赵爽弦图拼法 (b - a)2 中黄实 c a b 朱实 2 2 4 ( ) 4 2 S S S abc b a 大正方形 小正方形 直角三角形 c a b 化简得: c2 =a2+ b2. 结论 勾股定理:如果直角三角形两直角边分别为a、b, 斜边为c,那么 a2+b2=c2. a b c 解决实际问题:应用列举 例1、如下图,受台风影响,一棵树在离地面4米处断裂,树的 顶部落在离树根底部3米处,这棵树折断前有多高? 解:在直角△ABC中,由勾股定理得: 2534 22222 BCABAC 因此,AC=5 所以,折断前树高为AC+AB=5+4=9(米) 4米 3米 A B C 基本练习 1 2 3S S S 1.如图,分别以Rt△ABC 三边为边向外作三个正 方形,其面积分别用S1、 S2、S3表示,容易得出S1、 S2、S3之间有的关系式 为 . 课堂小结 谈谈你的收获! 勇敢的说一说! 1.这节课你的收 获是什么? 2.理解“勾股定 理”应该注意什 么问题? 3.你觉得“勾股 定理”有用么? 作用在哪里? 老师寄语 希望你们好好学习! 要养成用数学的思维去解读世界的习惯。 只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。 其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们 的身边,我们的眼前, 还有很多像 “勾股定理”那样的知识等待着我们去探 索,等待着我们去发现…… 作业快餐 作业一 作业二 作业三 作业四 •完成课本习题18.1(1、2、 3)(必做) •课后小实验:如图,分别以 直角三角形的三边为直径作 三个半圆,这三个半圆的面积 之间有什么关系?为什么? (必做) •做一棵美丽的勾股树(选做) •同学们课后探讨证明勾股定 理的其他方法 (选做) 感谢聆听 敬请指导查看更多