第8章 第3节 电路动态变化问题-2021年初中物理竞赛及自主招生大揭秘专题突破

第8章 第3节 电路动态变化问题-2021年初中物理竞赛及自主招生大揭秘专题突破

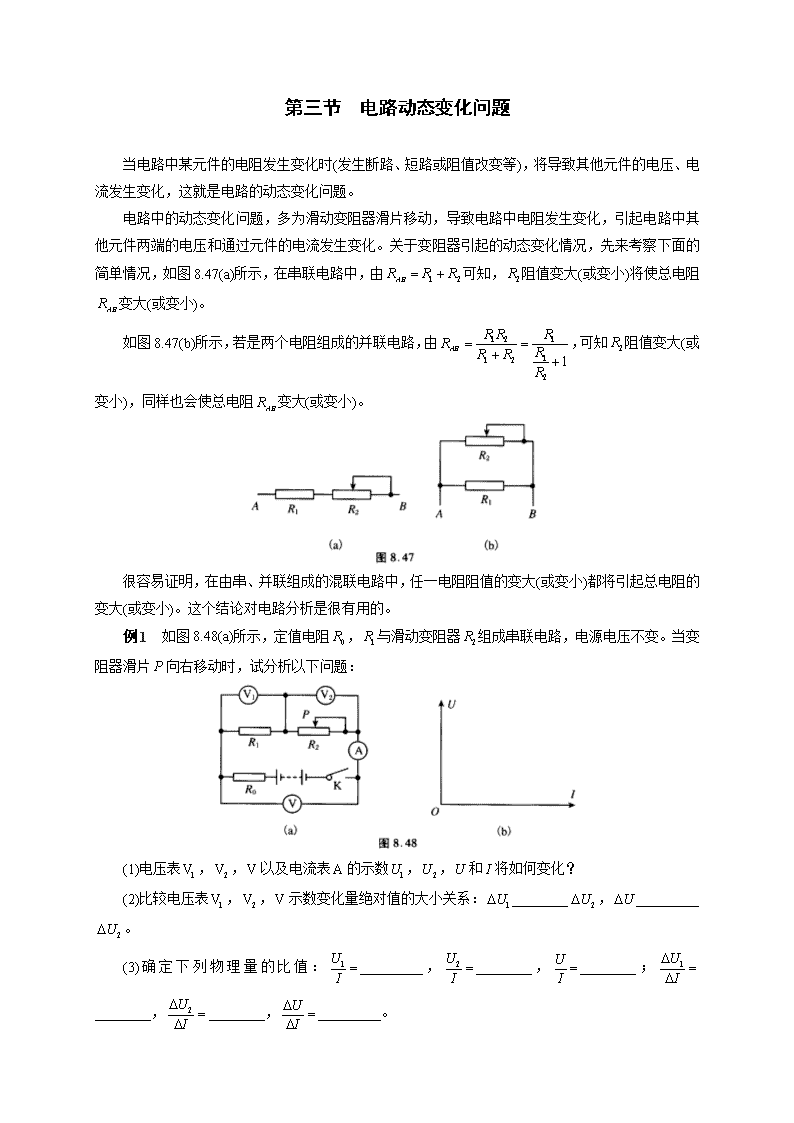
第三节 电路动态变化问题 当电路中某元件的电阻发生变化时(发生断路、短路或阻值改变等)，将导致其他元件的电压、电 流发生变化，这就是电路的动态变化问题。 电路中的动态变化问题，多为滑动变阻器滑片移动，导致电路中电阻发生变化，引起电路中其 他元件两端的电压和通过元件的电流发生变化。关于变阻器引起的动态变化情况，先来考察下面的 简单情况，如图 8.47(a)所示，在串联电路中，由 1 2ABR R R  可知， 2R 阻值变大(或变小)将使总电阻 ABR 变大(或变小)。 如图 8.47(b)所示，若是两个电阻组成的并联电路，由 1 2 1 11 2 2 1 AB R R RR RR R R    ，可知 2R 阻值变大(或 变小)，同样也会使总电阻 ABR 变大(或变小)。 很容易证明，在由串、并联组成的混联电路中，任一电阻阻值的变大(或变小)都将引起总电阻的 变大(或变小)。这个结论对电路分析是很有用的。 例 1 如图 8.48(a)所示，定值电阻 0R ， 1R 与滑动变阻器 2R 组成串联电路，电源电压不变。当变 阻器滑片 P 向右移动时，试分析以下问题： (1)电压表 1V ， 2V ， V 以及电流表 A 的示数 1U ， 2U ，U 和 I 将如何变化？ (2) 比 较 电 压 表 1V ， 2V ， V 示 数 变 化 量 绝 对 值 的 大 小 关 系 ： 1U ________ 2U ， U _________ 2U 。 (3)确定下列物理量的比值： 1U I  _________， 2U I  ________，U I  ________； 1U I   ________， 2U I   ________， U I   _________。 (4)若滑片 P 从最左端缓慢滑到最右端，在图 8.48(b)中画出 1U ， 2U ，U 随电流 I 的图像，并标 清楚关键点的坐标。设电源电压为U总 。 分析与解 (1)滑片 P 向右滑动时，变阻器电阻连人电路部分的阻值变大，则整个电路的总电阻 变大，因此电路中的电流 I 减小，定值电阻 0R ， 1R 两端的电压分别为 0 0U IR ， 1 1U IR ，则 0U ， 1U 减小；而 2R 阻值变大，I 减小，由 2 2U IR 无法判断出 2U 的变化情况。可这样考虑： 0U ， 1U 与 2U 之 和等于电源电压U总 ，则  2 0 1U U U U  总 ，可见 2U 增大。又 0U U U 总 ，所以U 增大。 (2)考虑到 1 2U U U  ，且 1U 减小、 2U 增大、U 增大，因此 1 2U U   ，且 2U U   . (3)根据欧姆定律，有 1 1 U RI  ， 2 2 U RI  ， 1 2 U R RI   。由于电阻 1R 为定值电阻， 1U 1IR ， 1U I 图像为正比例函数图像，则斜率 1 1 U RI   ；考虑到 2 2U IR ， 2R 不是定值，因此 2 2 U RI   ，由于    2 0 1 0 1U U U U U I R R     总 总 ，可见 2U I 图像也为直线，其斜率绝对值 2 0 1 U R RI    ；同 理， 0 0U U U U IR   总 总 ， 0 U RI   。 (4) 1R 两端的电压 1 1U IR ， 1U I 的图像如图 8.49 中图线 1 所示；变 阻器 2R 两端的电压  2 0 1U U I R R  总 ， 2U I 的图像如图线 2 所示；电 压表 V 的示数 0U U IR 总 ，U I 的图像如图线 3 所示。值得注意的是， 当 滑 动 变 阻 器 阻 值 取 得 最 大 值 2R 时 ， 电 路 中 电 流 取 得 最 小 值 2 min 0 1 U RI R R  总 ；当滑动变阻器阻值 2 0R  时，电路中电流取得最大值 maxI  0 1 U R R 总 ，实际上电流只会在 minI 与 maxI 之间变化，因此在 min0 ~ I 范围内的图像用虚线表示。 直线 2，3 的截距均为电源电压U总 ，当 2 0R  时， 2 0U  ，此时电压表 1V 与 V 示数相同，即 1U U ， 对应图线 1，3 的交点儿 A 。当 2 0R  时， 2V 与 1V 示数相同， 2 1U U ，对应直线 1，2 的交点 B 。 例 2 如图 8.50 所示，电源电压不变，闭合电键，将滑动变阻器 2R 的滑片向下滑动，理想电压 表 3V 示数变化量的绝对值为 3U ，理想电流表 1A ， 2A 的示数变 化量的绝对值分别为 1I ， 2I ，则( )。 A． 2A 示数增大 B． 2V 示数与 1A 示数的比值减小 C． 3U 与 1I 的比值小于 12R D． 1I 小于 2I 分析与解 由电路图可知， 1R 与 2R 并联，然后再与 3R 和 4R 串联，电压表 3V 测量并联部分的电 压，电压表 1V 测量 3R 两端电压，电压表 2V 测量并联部分与 3R 两端电压之和。电流表 1A 测通过电條 的总电流， 2A 测通过 2R 的电流。当变阻器 2R 的滑片向下滑动时， 1R 与 2R 的并联电阻变小，则电路 总电阻变小，总电流 1I 变大，因此 3R 与 4R 两端电压均变大，则 1R 两端电压变小，即 3V 的示数变小； 2V 的示数等于电源电压与 4R 两端电压之差，则 2V 的示数变小； 1V 的示数变大。 电流表 1A 的示数 1I 等于电流表 2A 的示数 2I 与通过 1R 的电流 1RI 之和，即 11 2 RI I I  ，由 1I 增大， 1RI 减小，可知 2I —定增大，且 2I 的增加量 2I —定大于 1I 的增加量 1I ，选项 AD 正确；电压表 2V 的 示数与电流表 1A 的示数的比值等于 1R ， 2R 和 3R 的等效电阻，显然三者的等效电阻变小，选项 B 正 确，由于 3V 的示数 3 1 3 4( )U U I R R   ，可见 3 3 4 1 U R RI    ，与 12R 的关系不能确定，因此选项 C 错误，正确选项为 ABD。 例 3 如图 8.51 所示，电源电压U 不变， 0R ， 1R 均为定值电阻，滑 动变阻器的最大阻值为 R ，在变阻器滑片 P 由 b 端缓慢滑到 a 端的过程 中，试求： (1) A ， B 两点间的电阻 ABR 的变化情况。 (2)电流表 A ， 1A ， 2A 示数的变化情况。 分析与解 (1)由电路图可知， 1R 与滑动变阻器的 Pb 部分并联，再与 Pa 部分串联，不妨设 PbR x ， 则 PaR R x  ，当滑片由 b 向 a 端滑动时， x 增大， A ， B 间的阻值 2 1 11 1 2 1 1AB R x xR R x R R RR x R x x x          显然，当 x 增大时， ABR 减小。 (2)设 A ， 1A ， 2A 的示数分别为 I ， 1I ， 2I ，则由并联电路的规律，有 1 2I I I  ， 1 1 2I R I x ， 解得 1 1 xI IR x   ， 1 2 1 RI IR x   。 由欧姆定律，得 0AB UI R R   ，所以 x 增大时， ABR 减小， I 增大。 1 2 1 1 0 1 0 1 AB x x U x UI I xR x R x R R R x R R R x                  2 2 0 1 0 1 0 Ux Ux R R R x x x R R x R R R             1 0 0 U R R Rx R R x      可见，当 x 增大时，上式分母减小， 1I 增大。又 1 1 1 2 2 1 1 0 1 0 1 AB R R RU UI I xR x R x R R R x R R R x                   1 1 2 2 0 1 0 0 1 UR UR R R R x x x R R x R R R          上 述 2I 表 达 式 中 的 分 母 为 关 于 x 的 二 次 函 数 ， 易 得 当 0 2 R Rx  时 ， 2I 取 得 最 大 值 2maxI    1 0 1 0 4 4 UR R R R R R     。但实际上滑动变阻器的最大阻值为 R ，0 x R„ „ ，因此应做如下讨论： ①若 x 取得最大值 R 时，仍有 0 2 R Rx  „ ，即 0R R„ ，则 2I 表达式的分母一直变大， 2I 减小。 ②若 x 取得最大值 R 时，已经出现 0 2 R Rx  ，即 0R R ，则 2I 表达式的分母先变大后变小， 2I 将先变小，后变大。 例 4 在如图 8.52 所示的电路中，已知电源电压U 不变，电阻 1R 的 阻值小于滑动变阻器的最大阻值 0R 。闭合电键S ，在滑动变阻器的滑片 P 由最左端向右滑动的过程中，试分析以下问题。 (1)说明滑动变阻器滑片 P 由最左端向右滑动的过程中，电路总电 阻 R总 的变化情况，并指出 R总 取得极值的条件。 (2)试分析滑动变阻器滑片 P 由最左端向右滑动的过程中，电压表 1V ， 2V ，电流表 1A ， 2A ， 3A 示数的变化情况。 (3)试分析电压表 1V ， 2V 示数的变化量的绝对值 1U ， 2U 与电流表 3A 示数变化量绝对值 3I 的 比值是否为定值，并指出比值所代表的物理意义。 分析与解 (1)如图 8.52 所示，设滑动变阻器 Pb 段阻值为 x ，则 Pa 段阻值为 0R x ，电路中 AB 部 分 实 际 是 1R 与 Pa 段 电 阻 串 联 后 ， 再 与 Pb 段 并 联 ， 则 根 据 并 联 电 路 的 电 阻 规 律 ， 有 1 1 1 1 AB Pa PbR R R R   ，解出 ABR 并利用基本不等式，可得     2 1 1 1 1 1 1 2 4AB x R R x x R R x R RR R R R R              „ 当且仅当 1 0x R R x   时，即 1 0 2 R Rx  时，不等式取等号。由题意 1 0R R ，可知不等式可以取等 号， ABR 的最大值为 1 max 4AB R RR  。 因此外电阻 1 0 2 0 2maxmax 4ABR R RR R RR R     总 。 所以滑动变阻器滑片 P 由最左端向右滑动的过程中，外电路总电阻 R总 先变大再变小。 (2)由(1)的分析可知，滑片 P 由最左端向右滑动的过程中， ABR 以及电路总电阻 R总 先变大再变小， 总电流 I 先变小再变大，因此电流表 3A 的示数先变小再变大，电压表 2V 的示数先变小再变大。电压 表 1V 的示数先变大再变小。 对于电流表 1A ， 2A 的示数 1I ， 2I 的变化，可以采用下列方式分析： 设滑片在位置 O 时， A ， B 间电阻达到最大值 maxABR 。 ①滑片由 a 滑向 O 时， ABR 逐渐增大，因此 ABU 逐渐增大而总电流 I 减小， 1A 的示数 1I AB Pb U R  ， 由于 PbR 逐渐减小，则 1I 增大。又 1 2I I I  ，可知在 1I 增大而 I 减小的情况下， 2I 必然减小。 ②滑片由 O 滑向 b 时， ABR 逐渐减小，因此 ABU 逐渐减小而总电流 I 增大， 2A 的示数 2I Pa ABU R  ， 由于 PaR 逐渐增大，则 2I 减小。又 1 2I I I  ，可知在 2I 减小而 I 增大的情况下， 1I 必然增大。 综上所述，滑片 P 由最左端向右滑动的过程中，电压表 1V 的示数先增大后减小， 2V 的示数先减 小后增大，电流表 1V 的示数一直增大， 2V 的示数一直减小， 3A 的示数先变小后变大。滑动变阻器 的这种接法对两支路的电流表变化情况可记忆如下：滑片向哪个方向滑动，哪边支路的电流变大， 另一支路的电流变小。 (3)电压表 1V ， 2V 的示数 1U ， 2U 与电流表 3A 的示数 3I 满足一定的函数关系，可以先根据电路 中电流、电压的关系写出它们的关系： 1 3 0U U I R  ， 2 3 2U I R ，由此可见， 1U ， 2U 与 3I 均为线性 关系，比值 1 3 U I   ， 2 3 U I   即为直线斜率的绝对值。则 1 0 3 U RI   ， 2 2 3 U RI   。 从前面几个例题可以看出，对于动态电路问题，往往要以阻值发生变化的电阻为突破口，例如， 可以按照滑动变阻器滑片滑动→变阻器连入电路部分阻值变化→总电阻变化→总电流变化→某部分 电压变化→变阻器所在部分电压变化→变阻器所在支路电流变化的思路来思考，即局部→整体→局 部的策略。 对于电压变化量 U 与电流变化量 I 的比值问题，要与电压U 与电流 I 的比值区别开来。一般 凡是遇到 U I   问题，都要写出U 与 I 的关系式，利用一次函数的斜率 Uk I   来求解。另外要注意可 变电阻的U 与 I 的关系(斜率为负的一次函数)与定值电阻的U 与 I 的关系(正比例函数)的区别。 练习题 1．(上海第 29 届大同杯初赛)下图中，通过滑动变阻器可以调节灯泡亮度的电路图是( )。 A． B． C． D． 2．(上海第 14 届大同杯初赛)在下图所示的电路中，AB 为粗细均匀的长为 L 的电阻丝，以 AB 上 各点对 B 点的电压U 为纵坐标，各点距 A 点的距离为横坐标，则U 随 x 变化的图线应为( )。 A． B． C． D． 3．(上海第 14 届大同杯初赛)如图 8.53 所示， 1 20 R   ， 2 25 R   ，当电键 1K 闭合、 2K 断开 时，电压表的示数为 2.8 V ，当电键 1K 断开、 2K 闭合时，电压表示数可能的数值是( )。 A． 4.0 V B．3.5 V C． 3.3 V D． 2.5 V 4．(上海第 19 届大同杯初赛)在图 8.54 所示的电路中，电源电压为 4.5 V ，且保持不变，电阻 1R 的阻值为 5  变阻器 2R 的最大阻值为 20  ，电流表的量程为 0 ~ 0.6 A ，电压表的量程为 0 ~ 3 V 。 为保护电表，变阻器接入电路的阻值范围是( )。 A． 2.5 ~ 10  B． 0 ~ 20  C． 2.5 ~ 20  D． 0 ~ 10  5．(上海第 23 届大同杯初赛)在图 8.55 所示的电路中，电源电压保持不变，当闭合电键 S 后， 将滑动变阻器的滑片向左滑动时( )。 A．灯 1L ， 3L 变亮，灯 2L 变暗 B．灯 1L ， 2L 变亮，灯 3L 变暗 C．灯 2L ， 3L 变亮，灯 1L 变暗 D．灯 1L ， 2L ， 3L 都变亮 6．(上海第 19 届大同杯初赛)在图 8.56 所示的电路中，当滑动变阻器的滑片 P 移动时，电压表 2V 的读数变大，则下列关于其他电表读数变化情况的说法中，正确的是( )。 A． 1V ， A 读数均变大 B． 3V ， V 读数均变大 C． V ， A 读数均变大 D． 3V ， 1V 读数均变大 7．(上海第 13 届大同杯初赛)如图 8.57 所示，闭合电键 K ，当滑动变阻器的滑片 P 在某两点之 间来回滑动时，电流表的示数范围是1.0 ~ 2.0 A ，电压表的示数范围是 7.2 ~ 2.4 V ，则电源电压为 ( )。 A．15 V B．12 V C．10 V D．无法判定 8．(上海第 12 届大同杯初赛)在图 8.58 所示的电路中，闭合电键 K ，当滑片 P 向右移动时( )。 A．电压表读数变小，电流表读数变大 B．电压表读数变大，电流表读数变小 C．电压表读数不变，电流表读数变大 D．电压表读数不变，电流表读数变小 9．(上海第 24 届大同杯初赛)在图 8.59 所示的电路中，电源电压保持不变。下列关于电路故障 的判断，正确的是( )。 A．若 1R 断路，电流表示数变小，电压表示数为零 B．若 2R 断路，电流表示数变小，电压表示数变大 C．若 3R 断路，电流表示数为零，电压表示数变小 D．若 4R 短路，电流表示数变小，电压表示数变大 10．(上海第 16 届大同杯初赛)如图 8.60 所示，电源电压保持不变， 0R 为定值电阻，闭合电键 K ， 电压表的示数为 0U 。移动滑动变阻器 R 的滑动触头 P ，使得变阻器的电阻值减小为原来的 1/3 时， 电压表的示数将由 0U 。增大到 02U ，则下列说法中错误的是( )。 A．通过滑动变阻器 R 的电流增大为原来的 2 倍 B． 0: 3:1R R  C．滑动变阻器 R 两端的电压减为原来的 1/3 D．当滑动触头 P 滑到 R 的最右端时，电压表的示数为 04U 11．如图 8.61 所示，电源电压不变，闭合电键S 后，将滑动变阻器 0R 滑片向下滑动，理想电压 表 1V ， 2V ， 3V 的示数变化量的绝对值分别为 1U ， 2U ， 3U ，理想电流表 A 的示数变化量的绝 对值为 I ，则( ) A．电流表 A 的示数减小 B． 1 2U U   C． 3U rI   D． 2 1 3U U U     12．(上海第 32 届大同杯初赛)在如图 8.62 所示的电路中，电源电压保持不变， 1 1 R   ， 2 3 R   。 闭合电键S 后，移动滑动变阻器 3R 的滑片 P ，使电压表 1V ， 2V ， 3V 示数的变化量的绝对值分别为 1U ， 2U ， 3U ，若 1 0.3 VU  ，则( )。 A． 2 0.1 VU  ， 3 0.2 VU  B． 2 0.4 VU  ， 3 0.1 VU  C． 2 0.2 VU  ， 3 0.4 VU  D． 2 0.1 VU  ， 3 0.4 VU  13．(上海第 32 届大同杯初赛)在如图 8.63 所示的电路中，电路两端电压恒定， 0R 为定值电阻， 1R 为滑动变阻器，且其最大阻值满足 1 02R R 。当变阻器 1R 的滑片 P 由最左端 a 滑到最右端 b 的过 程中( )。 A． 1A 表示数一直变小， 2A 表示数先变大后变小 B． 1A 表示数一直变小， 2A 表示数一直变大 C． 1A 表示数先变小后变大， 2A 表示数先变大后变小 D． 1A 表示数先变小后变大， 2A 表示数一直变大 14．(上海第 32 届大同杯初赛)在图 8.64(a)所示的电路中， 0R ， 1R 均为定值电阻， 1 4 R   。电 源电压U 保持不变，在滑动变阻器 2R 的滑片 P 由 a 端移动到b 端的过程中，电流表 1A ， 2A 的示数 1I 与 2I 对应关系所得到的完整图线如图 8.64(b)所示，其中 C 点位于图线最低点，对应的横坐标和纵坐 标分别为1.0 A 和 0.50 A ， A 点对应的横坐标为 0.75 A ，则( )。 A．电源电压U 的大小为 6 V B．滑动变阻器 2R 的最大阻值为8  C．图 8.64(b)中 A 点对应的纵坐标为 0.75 A D．图 8.64(b)中 B 点对应的纵坐标为 0.75 A 15．(上海第 31 届大同杯初赛)在如图 8.65 所示的电路中，电源电压U 保持不变， 1R ， 2R ， 3R 为 定值电阻，移动滑动变阻器的滑片，使电压表 1V ， 2V 的示数分别增大 1U ， 2U 在这个过程中( )。 A． 2 1U U   B．通过电阻 1R 的电流增加 1 1/U R C．通过电阻 2R 的电流减小 2 3/U R D．电阻 3R 两端的电压增大 2U 16．(上海第 30 届大同杯初赛)在如图 8.66 所示的电路中，无论电路中的电阻如何变化，设定流 入电路的总电流始终保持恒定。当变阻器 0R 的滑动触头向上滑动时，电压表 V 、电流表 V 的示数变 化量分别为 U ， I ，则 U I   为( )。 A． 1R B． 2R C． 1 2R R D． 1 2R R 17．(上海第 29 届大同杯初赛)在如图 8.67 所示的电路中，电源电压U 保持不变。电路中的定值 电阻阻值 R 大于 0R 。将滑动变阻器滑片向下滑动，电压表 1V ， 2V ， 3V 示数的变化量的绝对值分别 为 1U ， 2U ， 3U ，电流表 A 示数的变化量的绝对值为 I ，则( )。 A．电流表 A 的示数增大 B．电压表 2V 的示数增大 C． 1U 大于 2U D． 2U 与 I 的比值大于 0R 18．(上海第 28 届大同杯初赛)某同学做电学实验，改变滑动变阻器接入电路的电阻大小，并测 量记录了多组电压表和电流表的示数，根据数据分析，连接的电路可能是下面电路中的( )。 / VU 0.6 0.7 0.8 0.9 1.0 1.1 / AI 0.18 0.21 0.25 0.27 0.30 0.33 A B C D 19．(上海第 28 届大同杯初赛)在图 8.68 所示的电路中，灯 1L ， 2L 的电阻分别为 1R ， 2R ，变阻 器的最大电阻为 0R ，灯的电阻保持不变，当变阻器的滑片 P 由 a 端向 b 端移动时，灯 1L ， 2L 的亮度 变化情况是( )。 A．当 2 0R R 时， 1L 变暗， 2L 变亮 B．当 2 0R R 时， 1L 先变暗后变亮， 2L 先变亮后变暗 C．当 2 0R R 时， 1L 先变暗后变亮， 2L 先变亮后变暗 D．当 2 0R R 时， 1L 先变备后变亮， 2L 不断变亮 20．(上海第 27 届大同杯初赛)在如图 8.69 所示的电路中， 0R ， 1R 为定值电阻， 2R 为滑动变阻 器。闭合电键S ，当滑动变阻器的滑片 P 向下滑动时，四个理想电表的示数都发生变化，电表的示 数分别用 I ， 1U ， 2U 和 3U 表示，电表示数的变化量分别用 I ， 1U ， 2U 和 3U 表示，则在滑片 P 向下滑动的过程中( )。 A． 1U I 不变， 1U I   不变 B． 2 1 3U U U  C． 3U I 不变， 3U I   不变 D． 2 1 3U U U     21．(上海第 27 届大同杯初赛)设计一个如图 8.70 所示的电路 a 表示定值电阻，b 表示滑动变阻 器，电源电压保持不变。其中，有阻值分别为 1R ， 2R 的两个定值电阻可供 a 选择，有最大阻值分别 为 3R ， 4R 的两个滑动变阻器可供 b 选择，且 1 2 3 4R R R R   。要求：在移动变阻器滑片 P 的过程中， 电流表示数的变化量最大。则正确的选择是( )。 A． a 选 1R ，b 选 4R B． a 选 1R ， b 选 3R C． a 选 2R ， b 选 3R D． a 选 2R ， b 选 4R 22．(上海第 26 届大同杯初赛)在图 8.71(a)所示的电路中，电源电压U 保持不变， 1R ， 2R 为定 值电阻，R 为滑动变阻器，闭合电键S ，将滑动变阻器的滑片 P 从右端滑到左端的过程中，电压表 1V ， 2V 的示数随电流表 A 的示数变化的完整图线如图 8.71(b)中①，②图线所示。下列选项中能正确反映 该过程中电压表 3V 的示数随电流表 A 的示数变化的完整图线的是( )。 A B C D 23．(上海第 20 届大同杯初赛)在图 8.72(a)所示电路中， 0R ， 2R 为定值电阻，电流表、电压表 都是理想电表。改变滑动变阻器 1R 的滑片位置，电压表 1V ， 2V 和电流表 A 的示数均要发生变化。 两电压表示数随电流表示数的变化图线如图 8.72(b)所示。则下列判断中正确的是( )。 A．电压表 1V 示数变化图线为 a ，且电阻 0R 为1  B．电压表 1V 示数变化图线为 a ，且电阻 0R 为 2  C．电压表 1V 示数变化图线为 b ，且电阻 0R 为1  D．电压表 1V 示数变化图线为 b ，且电阻 0R 为 2  24．(上海第 22 届大同杯初赛)在如图 8.73 所示的电路中，电源电压保持不变， 0R ， 1R 和 3R 均 为定值电阻， 2R 为滑动变阻器。当 2R 的滑片在 a 端时，闭合电键S ，三个电表 1A ， 2A 和 V 的示数 分别为 1I ， 2I 和U 。现将 2R 的滑片向 b 端移动，则三个电表示数的变化情况是( )。 A． 1I 增大， 2I 不变，U 增大 B． 1I 减小， 2I 增大，U 减小 C． 1I 增大， 2I 减小，U 增大 D． 1I 减小， 2I 不变，U 减小 25．(上海第 21 届大同杯初赛)如图 8.74 所示，电源电压保持不变。当滑动变阻器的滑片 P 向左 移动时，电压表和电流表的示数变化情况是( )。 A． 1A 增大， 1V 减小 B． 2A 增大， 2V 减小 C． 1A 减小， 1V 减小 D． 2A 增大， 2V 增大 26．(上海第 20 届大同杯初赛)在如图 8.75 所示的电路中，电源电压不变，电流表、电压表都是 理想电表，当滑动变阻器 R 的滑片 P 从 a 端移到 b 端的过程中( )。 A． V 表示数先减小后增大， A 表示数增大 B． V 表示数先增大后减小， A 表示数减小 C． V 表示数先减小后增大， A 表示数先增大后减小 D． V 表示数先增大后减小， A 表示数先减小后增大 27．(上海第 20 届大同杯初赛)如图 8.76 所示， AB ， CD 为两根平行且均匀的相同电阻丝，直 导线 EF 可以在 AB ，CD 上滑行并保持与 AB 垂直， EF 与 AB ， CD 接触良好。 B ， D 之间的电压 U 保持不变， A ，C 之间接一个理想电压表，当 EF 现处于图中位置时电压表示数为 6.0 V ，将 EF 由图中位置向左移动一段距离 L 后电压表示数变为 5.0 V ，若将 EF 由图中位置向右移动一段相同 距离 L 后，电压表示数将变为( )。 A． 6.5 V B． 7.0 V C． 7.5 V D．8.0 V 28．(上海第 20 届大同杯初赛)在图 8.77 所示的电路中，电源电压恒定，滑片 P 把变阻器分为 5 PaR   ， 10 PbR   两部分，要求当电键 K 闭合时，c ，d 间的电压不得低于电键断开时 c ，d 间 电压的 90% ，则电阻 xR 的允许取值范围是( )。 A． 10 xR „ B． 30 xR „ C． 10 xR … D． 30 xR … 29．(上海第 20 届大同杯初赛)在图 8.78 所示的电路中， A ， B 两点之间电压U 保持不变，电 路连接完好且使用的电表均为理想电表。当滑动变阻器的滑片 P 向右滑动时( )。 A．电压表 1V 和电流表 A 的示数之比增大 B．电压表 2V 和电流表 A 的示数之比不变 C．电压表 1V 示数的变化量和电流表 A 示数的变化量的比值的绝对值 1U I   增大 D．电压表 2V 示数的变化量和电流表 A 示数的变化量的比值的绝对值 2U I   不变 30．(上海第 16 届大同杯初赛)某同学在实验室按图 8.79 所示电路进行实验，当把滑动变阻器的 滑动触头 P 分别滑到 a ，b ，c ，d 四个位置时，记下每个位置所对应的电流表和电压表的示数。当 他回到教室对测量数据进行分析时，才发现由于自己在记录数据时的不规范和随意性，只记录了电 流表的示数分别为 4 / 3 A 、6 / 5 A 、2 / 3 A 和1 A ；电压表的示数分别为 6 V 、8 V 、4 V 和 4.8 V 。 但电表示数之间的对应关系、电表示数和滑动触头 P 所处位置之间的对应关系均已搞不清楚。假如 该同学实验测得的数据是准确的，则可以分析出当滑动触头 P 滑到 b 位置时电流表和电压表的示数 应该是( )。 A． 4 / 3 A ，8 V B．1 A ， 6 V C． 6 / 5 A ， 4 V D． 2 / 3 A ， 4.8 V 31．(上海第 16 届大同杯初赛)在图 8.80 所示电路中，电源电压保持不变。 1R ， 2R 均为定值电 阻。当滑动变阻器 R 的滑动触头 P 由左向右移动时( )。 A．电流表 1A 示数始终在增大，电流表 2A 示数先减小后增大 B．电流表 2A 示数始终在增大，电流表 1A 示数先减小后增大 C．电流表 1A 示数先增大后减小，电流表 2A 示数先减小后增大 D．电流表 2A 示数先增大疴减小，电流表 1A 示数先减小后增大 32．(上海第 13 届大同杯初赛)在如图 8.81 所示电路中，电源电压保持不变，当滑动变阻器的滑 片 P 自 a 向b 移动的过程中，图中各电表示数变化的情况是( )。 A． 1A ， 2A 变大， V 变小 B． A ， 1A ， V 变大， 2A 变小 C． A ， 2A ， V 变小， 1A 变大 D． A ， 1A ， V 变小， 2A 变大 33．(上海第 24 届大同杯初赛)在图 8.82(a)所示的电路中，电源 电压保持不变。将滑动变阻器 R 滑片 P 由 a 端移到 b 端，电压表 1V ， 2V 的示数与电流表 A 示数的变 化关系图线如图 8.82(b)所示。根据图线可以知道，滑动变阻器 R 的最大阻值为________  ，定值电 阻 2R 的阻值为_______  。 34．(上海第 23 届大同杯初赛)在图 8.83(a)所示的电路中，电源电压保持不变， 1R 为定值电阻， 2R 为滑动变阻器。闭合电键S ，调节滑动变阻器，将滑动变阻器的滑动触头 P 从最左端滑到最右端， 两电压表的示数随电路中电流变化的完整过程图线如图 8.83(b)所示。则图线________(填“甲”或“乙”) 是电压表 2V 示数随电流变化的图线。滑动变阻器的最大阻值为________  ，如果将定值电阻 1R 阻值 换为 20  ，同样将滑动变阻器的滑动触头 P 从最左端滑到最右端。请在图 8.83(c)中画出两电压表的 示数随电路中电流变化的完整过程图线。 35．(上海第 23 届大同杯复赛)在如图 8.84 所示的电路中，可以通过调整变阻器 R 和 R ，使通 过电阻 1R 和 2R 的电流达到规定的值 1I 和 2I ，并由电流表指示出其电流值。 正确的操作步骤是： ①电路接通前，变阻器的滑片应放在________(选填“ A ”或“ B ”)端，变阻器的滑片应放在 ________(选填“ a ”或“ b ”)端； ②电路接通后，先调节电阻________(选填“ R ”或“ R ”)，使电流表 1A 和电流表 2A 的示数 比值为 1 2/I I ，再调节________(选填“ R ”或“ R”)，使电流表_________(选填“ 1A ”或“ 2A ”) 的示数达到________(选填“ 1I ”或“ 2I ”)。 36．(上海第 9 届大同杯复赛)在图 8.85 所示的电路图中，定值电阻 1R 为 3  ，滑动变阻器 2R 的 最大阻值为12  ，电源电压恒定为 6 V ，电流表的电阻不计。求当滑片 P 移动时，电流表示数的变 化范围。 37．(上海第 7 届大同杯复赛)图 8.86 所示是一个分压电路。图中的负载电阻 1 160 R   ，允许 通过的最大电流是 0.15 A ，电源电压是14 V ，电压表的量程为 0 ~ 15 V ，滑动变阻器 ABR 上标有 “120  ， 0.15 A ”的字样。当滑片 P 自左向右移动时，电源电压保持不变，但电压表的示数会发 生变化。问： (1)电阻 1R 和 APR ， PBR 中哪一个通过的电流最大(说明理由)？ (2)滑片 P 在移动过程中(自 A 移向 B )，各元件是否安全(通过分析和估算电流加以说明)？ (3)在不损坏电路元件的前提下，电压表示数的变化范围是多少？ 参考答案 1．C。略。 2．C。设 AB 上一点 C 到 A 点的距离为 x ， C ， B 之间的距离为 L x 。设电阻丝 AB 的总阻值 为 R ，则 C ， B 之间的电阻为 ( )CB RR L xL   ，流过 AB 的电流 UI R  则 C ， B 之间的电压 ( )CB CB UU IR L xL    ，这是一个一次函数，选项 C 正确。 3．C。由于 2 1R R ，根据串联分压，当只闭合 2K 时，电压表读数应大于 2.8 V 。假设只闭合 1K 和只闭合 2K 时，电路中电流不改变，则只闭合 2K 时电压表的读数应为只闭合 1K 时的 5 4 倍，即为 5 2.8 V 3.5 V4   ，实际上由于电流要减小，电压表读数应小于 3.5 V 。综上所述，电压表读数应大 于 2.8 V 而小于3.5 V 。 4．A。电流表不超过 0.6 A ，则 4.5 V 0.6 A5 R  „ ，解得 2.5 R … ；电压表两端电压不超过 3 V ， 则 4.5 V 3 V5 RR   „ ，解得 10 R „ 。 5．B。变阻器与灯 1L 串联后，再与灯 3L 并联，最后并联部分再与 2L 串联。当变阻器滑片向左 滑动时，变阻器连入电路部分的阻值变小，并联部分总阻值变小，由分压关系可知，并联部分总电 压变小，灯 3L 的电压、电流均变小， 3L 变暗；由于整个电路的总电阻变小，总电流变大，所以灯 2L 变亮。灯 3L 的电流加上灯 1L 的电流等于总电流，可知 1L 的电流变大，灯 1L 变亮。 6．A。电压表 1V ， 2V ， 3V 分别测电阻 1R ， 2R ， 3R 两端的电压，电压表 V 测量 1R ， 2R ， 3R 的 电压之和。当 2V 读数变大时，说明电路中电流增大， A 表读数变大，则 1V 读数也变大。电路中电 流变大是滑动变阻器 3R 阻值减小引起的，根据串联分压规律，电阻 3R 减小，则 3V 读数变小；由于 4R 两端电压增大，电压表 V 的读数等于电源电压与 4R 两端电压之差，因此电压表 V 的读数减小。 7．B。随着变阻器阻值的变化，电压表示数U 与电流表示数 I 均发生变化，且 I 增大时，U 减 小。电源电压 0U U IR 总 ，当 7.2 VU  时， 1.0 AI  ；当 2.4 VU  时， 2.0 AI  ，代入联立解方 程，可得 12 VU 总 ， 0 4.8 R   。 8．C。电压表测电源电压，读数不变，滑动变阻器只有滑片右侧的部分连入电路，滑片向右移 动时，变阻器连入电路的阻值变小，电流表读数变大。 9．D。提示：若 1R 断路，则并联部分少了一个支路，并联部分总电阻变大， 3R 的电压、电流均 变大，且电压表由原来测 1R 的电压改为测 3R 的电压，电压表读数变大，选项 A 错误；若 2R 断路， 并联部分亦少了一个支路，则剩余并联部分总电阻变大，所分的电压也变大，使得电压表、电流表 读数均变大，选项 B 错误；若 3R 断路，则电流表示数为零，但电压表示数变大，选项 C 错误；若 4R 短路，则并联部分电阻变小，并联部分所分电压变小，通过电阻 2R ， 3R 的电流变小，但总电流变大， 因此通过电阻 1R 的电流要变大，电压表读数变大，选项 D 正确。 10．C。设电源电压为U ，开始时滑动变阻器接入电路的电阻为 1R ，则闭合电键 K 时： 1 1 0 UI R R   ， 0 0 1 0 1 0 URU I R R R    ，当变阻器的电阻值减小为 1 1 3 R 时： 2 1 0 1 3 UI R R   ， 02U 0 2 0 1 0 1 3 URI R R R    。将 0U 。 和 02U 的表达式两边相除，可解得 1 03R R ， 04U U ，且易得 2 12I I 。当滑动触头 P 滑到 R 的最 右端时，电压表的读数等于电源电压U 。因此只有选项 C 符合题意。 11．C。 0R 滑片向下滑动， 0R 阻值变小， 3V 的示数 3U 变小，又电路总电阻变小，电流表 A 的 示数 I 变大，选项 A 错误。 1V 的示数 1U 变大，电阻 r 两端的电压变大，则 2V 的示数 2U 变小，因为 2 1 3U U U  ，且 2 3 1U U U     ，因此无法判断 1U 与 2U 的大小关系，选项 BD 错误，结合 3 ( )U U I R r   ，可得 3U R r rI     ，所以选项 C 正确。 12．D。由三个电压表的示数与电流的函数关系： 1 2U IR ， 2 1U U IR  ， 3U U   1 2I R R ， 可 得 1 2 U RI   ， 2 1 U RI   ， 3 1 2 U R RI    ， 由 于 电 流 的 变 化 量 I 都 相 同 ， 因 此 1 2 3 2 1 1 2: : : : ( ) 3:1: 4U U U R R R R      ，由题意，解得 2 0.1 VU  ， 3 0.4 VU  ，选项 D 正确。 13 ． D 。 设 变 阻 器 Pa 部 分 的 阻 值 为 x ， 则 Pb 部 分 的 阻 值 为 1R x 。 电 路 总 电 阻 1R R x 总 2 0 1 1 00 0 2 1 1 R x xR R RR x R x x x        ，可见当滑片右移时， x 变大， R总 变小，则总电流变 大，即 2A 的示数变大。 通过 1A 的电流 0 00 1 2 2 0 0 0 0 1 1 0 R I U U RRI xR x R x x R x R RR R x          总 总 总 ，当 0 2 Rx  时， 1I 的表达式的 分母取得最大值， 1I 取得最小值。由于 1 02R R ，因此 x 的取值可以大于 0 2 R ，则滑片 P 由最左端向 最右端滑动时， 1I 应先变小，再变大。选项 D 正确。 14．AC。设 PbR x ，则 2PaR R x  ，当滑片由b 向 a 端滑动时， x 增大，因此，有 2 1 0 2 0 2 0 2 11 1 2 1 1 R x xR R R x R R R R RR x R x x x             总 显然，当 x 增大时， R总 减小，电流表 1A 读数 1I 随 x 的增大而增大。当 0x  时，即滑片在 b 点，此 时 1R 被短路， 1 2I I ，且 1I 取得最小值 0.75 A ，因此，图像上 A 点对应纵坐标为 0.75 A ，C 选项正 确。 由并联电路的电流规律，易得 1 1 1 2 2 2 1 1 0 2 1 0 2 1 ( )( ) R R URUI I xR x R x R R R x xR R R x           1 2 0 2 0 2 1( ) ( ) UR x R R x R R R       分析 2I 的分母可知，当 0 2 2 R Rx  时， 2I 取得最小值： 1 2min 0 1 0 4 0.5 A( )(4 ) URI R R R R R     ，对应 图 8.64(b)曲线上的 C 点，而此时通过电阻 1R 的电流 1 1 A 0.5 A 0.5 ARI    ，则可知 0 2 12 R Rx R  ， 所以 0 2 12 8 R R R    ，选项 B 错误。将 0 2 8 R R   代入到 2minI 的表达式，可知 6 VU  ，选项 A 正确。若图 8.64(b)中 B 点对应的纵坐标为 0.75 A ，则 2I  1 2 0 2 0 2 1 0.75 A( ) ( ) UR x R R x R R R      ， 将 0 2 8 R R   代入，解得 28 x R   选项 D 错误。 15．ABC。当 1V ， 2V 的示数分别增大时，说明滑片向左移动，变阻器 R 的阻值变大，则总电 阻变大，总电流变小，因此 2R ， 3R 两端的电压均减小，D 选项错误。设电阻 2R ， 3R 两端的电压分 别为 2U  ， 3U  ，由电路图可知， 1 2 2U U U  ， 1U 增大， 2U  减小， 2U 增大，因此 1U 的增大量大于 2U  的减少量，且 1U 增大量大于 2U 的增大量，即 1 2U U   ， 1 2U U   ，A 选项正确。由于 1R 为定值 电阻，通过 1R 的电流增加 1 1 U R  ，B 选项正确。又 2 3U U U  ，因此 2 3U U   ，所以通过电阻 2R 的 电流减小 3 2 3 3 U U R R   ，选项 C 正确。 16．A。要求出 U I   的值，最直接的方法是写出电压表读数U 与电流表读数 I 的函数关系式。 设流过电路的总电流为 0I ，则流过 1R 的电流为 0I I ，电压表的示数 0 2 0(U I R I   1)I R ，可得到U 与 I 的一次函数：  0 1 2 1U I R R IR   ，该直线的斜率的绝对值 1 U RI   。 17．AC。略，可参考本节例 2 的解法。 18．B。提示：由表格中数据可知， U I 等于定值，电压表和电流表应是测定值电阻的电压和电 流。 19．D。滑动变阻器的 Pb 部分与灯 2L 串联后再与变阻器的 Pa 部分并联，并联部分的总电阻 2 2 2 0 2 ( ) ( ) ( ) Pa Pb Pa Pb Pa Pb P R R P R RR R R R R R     并 ， R并 随滑片 P 的移动而变化，当 2Pa PbR R R  时， R并 取得最 大值。易得若使 2Pa PbR R R  成立，应有 2 0R R„ 。当 2 0R R 时，R并 将先变大，再变小，电路中的总 电阻也先变大后变小，因此通过 1L 的电流先变小后变大， 1L 先变暗后变亮。根据本小节例 3 的结论， 在滑动变阻器的这种接法中，滑片向左滑动，左边支路的电流增大，灯 2L 不断变亮。 20．AD。略，可参考本节例 1 的解法。 21．A。设电源电压为U ， a ，b 的阻值分别以 aR ， bR 表示，则 bR 当取零时，电流表的读数最 大： max a UI R  ，当 bR 取得最大值时，电流表的读数最小： min a b UI R R   ，则电流表示数的变化量  max min 2 b aa a b a a b a b R UU U UI I I RR R R R R R RR          ，可见， aR 越小，同时 bR 越大的情况下， I 越 大，即 a 应选 1R ， b 应选 4R 。 22．A。由题图可知，电路中电流的变化范围为 0.2 ~ 0.4 A ，图线①的延长线过坐标原点，结合 定值电阻 1R 两端电压与电流的关系： 1 1U IR ，因此图线①对应的是定值电阻 1R ，由图线①的斜率 可 求 得 1 1 4 2 10 0.4 0.2 UR I        。 结 合 变 阻 器 R 两 端 电 压 2U 与 电 流 I 的 关 系 ： 2 1 2( )U U I R R   ， 图 线 ② 对 应 的 是 2U 与 电 流 I 的 关 系 ， 因 此 可 得 2 1 2R UR I    3 0 15 0.4 0.2     ，则可知 2 5 R   。电压表 3V 测量的是变阻器 R 与电阻 2R 电压之 和 ， 当 0.2 AI  时 ， 3 2 2 3 V 0.2 5 V 4 VU U IR      ， 当 0.4 AI  时 ， 3 2 2 0 V 0.4U U IR    5 V 2 V  ，又 3 1U U IR  ， 3 1 10 U RI     ， 3U I 图像为直线，显然 选项 A 正确。 23．D。提示：电压表 1V 的示数与电流表 A 的示数关系为 1 0U U IR  ，电压表 2V 的示数与电 流表 A 的示数关系为 2 2U IR ，则图线 a 为电压表 2V 示数变化的图线，图线 b 为电压表 1V 示数变化 的图像。图线 b 的斜率的绝对值即为 0R 的阻值，则 0 10 V 4 V 2 4 A 1 AR    。 24．B。 2R 的滑片向 b 端滑动时， 2R 阻值变小，则 2R 与 1R 并联后的阻值 R并 变小，电压表 V 测 量并联部分与电阻 3R 的电压之和，由于 3R R并 变小，根据串联分压，可知 V 的示数变小。R并 变小， 则并联部分的电压U并 变小，可知流过电阻 1R 的电流 1I 变小，由于总电阻变小，总电流 I 变大， 1 2I I I  ，则 2R 的电流 2I 变小。 25．B。略，参照练习题 24 题的解答，注意电表的测量对象。 26．B。略，可参照本节例 4 的解法以及结论。 27．C。设 AB ，CD 导线单位长度的电阻为 r ，棒 EF 接入电路的阻值为 R ，再设初始 EF 到 BD 的距离为 L ，则 1 2 UI R Lr   ， 1 1 2 URU I R R Lr    。 当 EF 向左移动一段距离 L 后，有 2 2( ) UI R L L r     ， 2 2 2( ) URU I R R L L r      将 EF 由图 8.76 中位置向右移动 L 后，有 3 2( ) UI R L L r     ， 3 3U I R  2( ) UR R L L r   。 比较 1U ， 2U ， 3U 的倒数关系，不难得到： 2 1 1 3 1 1 1 1 U U U U    ，解得 3 7.5 VU  。 28．D。设电源电压为U ，则当 K 断开时， PaR 与 PbR 串联，故 2 3cd UU  ，当 K 闭合时， xR 与 PbR 并联后，再与 PaR 串联，则 Pb x Pb x Pa R RR R R R   总 ， Pb x Pa Pb x U UI R RR R R R     总 总 10 9 2 50 15 10 3 Pb x x cd Pb x Pb x x Ra Pb x R R URU UU I R R R R RR R R R        总 总 … 解得 30ΩxR … 。 29．D。略，可参考本节例 1 的解答和结论。 30．B。当滑片由 a 逐渐向 d 点滑动时，变阻器接入电路部分的阻值变大，变阻器与 1R 并联的部 分阻值变大，则 1R 两端电压增大，电流表 A 读数变大，对应地， 2R 两端电压变小，即电压表 V 读数 变小。可见，在滑片由 a 点逐渐向 d 点滑动的过程中，电流表读数逐渐变大，而电压表读数逐渐变 小。a ，b ，c ，d 四个位置所对应的电流、电压分别为( 2 / 3 A ，8 V )，(1 A ，6 V )，( 6 / 5 A ，4.8 V )， ( 4 / 3 A ， 4 V )。 31．A。画出等效电路如图 8.87 所示，滑动变阻器滑片左右两部分的阻值分别设为 aR ， bR ，则 aR ， bR ， 1R 三者并联，然后再与 2R 串联。设总电流为 I总 ， 1A ， 2A 的示数分别为 1I ， 2I ， 1A 测流经 bR 与 1R 的电流之和. 2A 测流 经 aR 与 bR 的电流之和。当滑片由最左端向最右端滑动时， aR 由 0 逐渐增大到 R ， aR 与 bR 并联之后的等效阻值 ||a bR 在 2a RR  时取 得最大值。下面分过程来讨论 1I ， 2I 的变化情况。 (1)当 aR 由 0 逐渐增大到 2 R 的过程中， ||a bR 增大，并联部分的总电阻 R并 增大，并联部分的电压U并 增大，则通过电阻 1R 的电流 1RI 增大，而 2R 上的电压变小，总电流 I总 变小，结合 12 RI I I  总 ，可知 2I 减小。再由U并 增大而 bR 减小，则 bRI 增大，故 11 bR RI I I  ，增大。 (2)当 aR 由只逐渐增大到 R 的过程中， ||a bR 减小，并联部分的总电阻 R并 减小，并联部分的电压U并 减小，则 1RI 减小。而 2R 上的电压增大，总电流 I总 增大，结合 12 RI I I  总 ，可知 2I 增大。由于U并 减 小， aR 变大，则 aRI 变小，结合 1 aRI I I  总 ，可知 1I 增大。 综上所述， 1I 一直增大， 2I 先减小后增大。 32．C。略。 33．9，2．略可参考本节例 1 的解答和结论。 34．乙，20，见图 8.88。由图 8.83(b)可知电源电压 1 2 6 VU UU   ， 电阻 1R 两端的电压 1 1U IR ，图像延长线为过原点的倾斜直线，因此甲 为 1R 的图线，且 1 1 UR I   6 2 10 0.6 0.2     。变阻器 2R 两端的电压 2 1U U IR  ，因此乙为 2R 的图线。结合图 8.88(b)可知，电流最小值 为 min 0.2 AI  ，此时变阻器阻值为最大值 2maxR ，则 minI  1 2 max U R R ， 解得 2max 20 R   。 当 1R 阻值换成 1 20 R   时，对应的最小电流 min 1 2max 6 A 0.15 A20 20 UI R R       ，此时滑动变 阻器阻值取得最大值 2max 20 R   ，变阻器两端电压 2max 3 VU  ， 1R两端电压 1minU 3 V 。电路中最 大电流 x 1 ma 6 A 0.3 A20I U R     ，此时变阻器阻值为零，两端电压为零， 1R 两端电压 1max 6 VU  。 两电压表的示数随电路中电流变化的完整过程图线如图 8.88 所示。 35.① B ， a ；② R ， R ， 21A (A ) ， 1 2( )I I 。电路接通前，为了防止干路电流过大，应将变阻 器 R 的滑片放在 B 端，变阻器 R的滑片应放在 a 端，则电路接通后，电流表 1A 读数为某一值，而电 流表 2A 读数为零。然后将 R的滑片从 a 向b 缓慢滑动， 1A 的读数会变小， 2A 的读数会变大，当观 察到 1A 和 2A 示数的比值为 1 2/I I 时，停止调节 R ，接着再调节 R 的滑片，容易得出当仅调节 R 的 滑片时， 1 2/I I 并不会发生变化，只需要使电流表 1A 的读数等于 1I ，或电流表 2A 的读数等于 2I ，即 可使通过电阻 1R 和 2R 的电流达到规定的值 1I 和 2I 。 36.设变阻器滑片右侧部分的阻值为 x ，则滑片左边部分的阻值为 R x ，电路总电阻 R总 2 1 1 1 R x xR x RR x R x       ，电路总电流 UI R  总 ，设电流表的读数为 AI ，通过电阻 1R 的电流为 1I ， 结 合 并 联 电 路 的 规 律 ， 有 A 1I I I  总 ， 1A 1I x I R ， 解 得 1 1 A 1 1 R RI IR x R x     1 2 2 1 1 URU x x Rx R RR R x      。 令 2 1y x Rx R R    ，代入数据并配方可得 2 212 36 ( 6) 72y x x x        ，考虑到 0 12x„ „ ， 可得 36 72y„ „ ，因此 A0.25 A 0.5 AI„ „ 。 37．(1)由题给电路图可知， 1R 和 APR 并联后，再与 PBR 串联，则通过 PBR 的电流为干路电流，最 大。 (2)由于电源电压为14 V ，电压表量程取 0 ~ 15 V ，电压表不会超出量程。 设电路总电流为 I总 ， APR x ，则 PB ABR R x  ，电路中的总电阻 R总 可表达为 2 1 11 1 2 1 1AB ABAB R x xR R x R R RR x R x x x          总 可见， x 越大， R总 越小。当 120 x   时， R总 取得最小值： 1 1 120 160 120 160 AB AB R R R R R   总 480 7   ， 因此最大总电流 max min 49 A 0.204 A 0.15 A240 UI R   总 总 。这样，滑动变阻器右端 PB 部分超过允许 通过的最大电流。 (3) 当 总 电 流 0.15 AI总„ 时 ， 电 路 中 各 元 件 方 能 不 损 坏 。 则 当 0.15 AI 总 时 ， 有 2 1 0.15 A AB U xI R R U R x     总 总 ， 代 入 数 据 ， 可 解 得 80 x   ， 此 时 通 过 1R 的 电 流 11 1 3I I  1 0.15 A 0.05 A3   ，则电压表读数 1 1 1 0.05 A 160 8 VU I R     ，当 0x  时， 1R 被短路， 1 0U  ，因此电压表的读数范围为 0 ~ 8 V 。