- 2021-05-27 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教版(理)第2章第8讲函数与方程作业
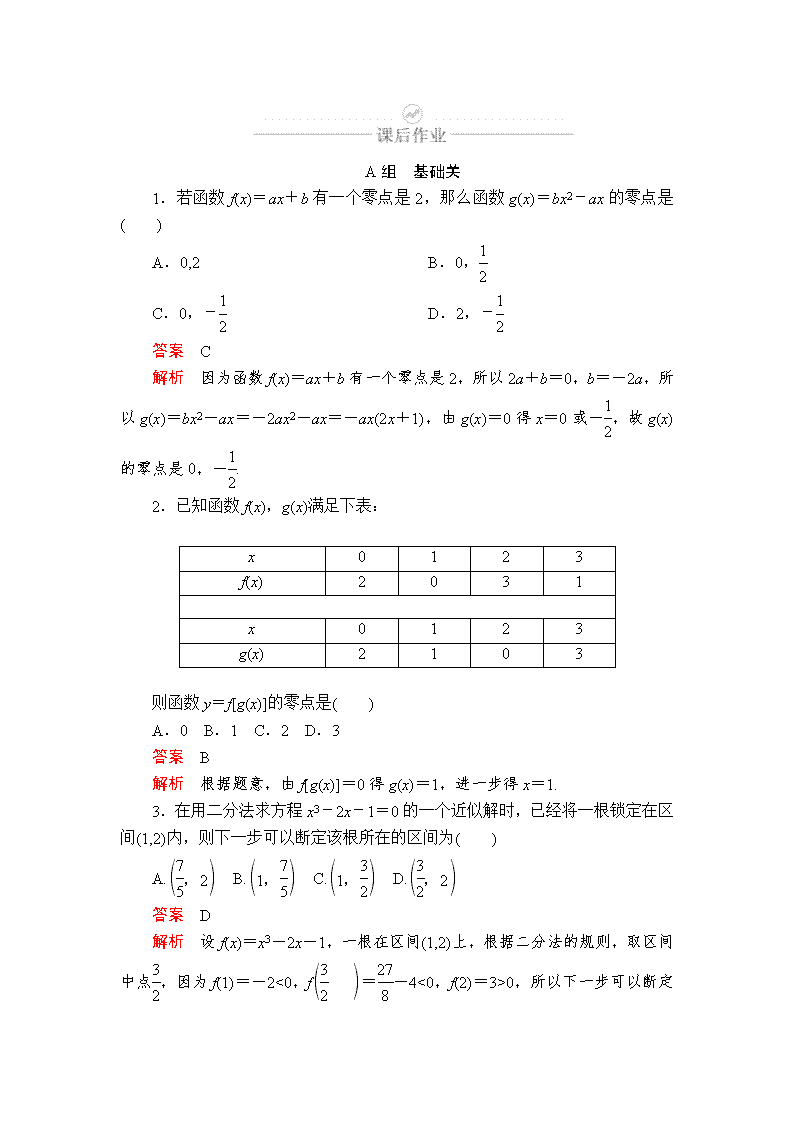
A组 基础关 1.若函数f(x)=ax+b有一个零点是2,那么函数g(x)=bx2-ax的零点是( ) A.0,2 B.0, C.0,- D.2,- 答案 C 解析 因为函数f(x)=ax+b有一个零点是2,所以2a+b=0,b=-2a,所以g(x)=bx2-ax=-2ax2-ax=-ax(2x+1),由g(x)=0得x=0或-,故g(x)的零点是0,-. 2.已知函数f(x),g(x)满足下表: x 0 1 2 3 f(x) 2 0 3 1 x 0 1 2 3 g(x) 2 1 0 3 则函数y=f[g(x)]的零点是( ) A.0 B.1 C.2 D.3 答案 B 解析 根据题意,由f[g(x)]=0得g(x)=1,进一步得x=1. 3.在用二分法求方程x3-2x-1=0的一个近似解时,已经将一根锁定在区间(1,2)内,则下一步可以断定该根所在的区间为( ) A. B. C. D. 答案 D 解析 设f(x)=x3-2x-1,一根在区间(1,2)上,根据二分法的规则,取区间中点,因为f(1)=-2<0,f=-4<0,f(2)=3>0,所以下一步可以断定该根所在的区间是,故选D. 4.若函数f(x)=2x--a的一个零点在区间(1,2)内,则实数a的取值范围是( ) A.(1,3) B.(1,2) C.(0,3) D.(0,2) 答案 C 解析 因为函数f(x)=2x--a在区间(1,2)上单调递增,又函数f(x)=2x--a的一个零点在区间(1,2)内,则有f(1)·f(2)<0,所以(-a)(4-1-a)<0, 即a(a-3)<0,解得0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档