九年级数学上册第四章图形的相似4探索三角形相似的条件第2课时利用两边及夹角判定三角形相似教学课件新版北师大版

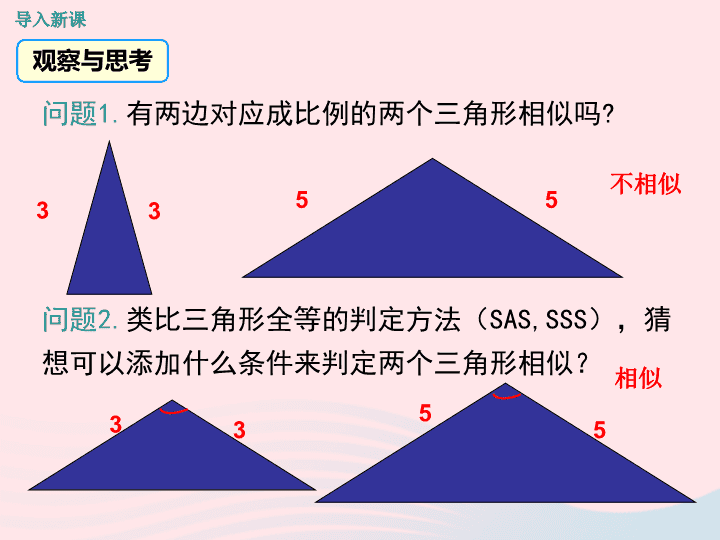
九年级数学上册第四章图形的相似4探索三角形相似的条件第2课时利用两边及夹角判定三角形相似教学课件新版北师大版

第四章 图形的相似 4.4 探究三角形相似的条件 第 2 课时 利用两边及夹角判定三角形相似 导入新课 讲授新课 当堂练习 课堂小结 学习目标 1. 掌握相似三角形的判定定理 2 ；（重点） 2. 能熟练运用相似三角形的判定定理 2 ．（难点） 问题 1 . 有两边对应成比例的两个三角形相似吗? 3 3 5 5 不相似 观察与思考 问题 2 . 类比三角形全等的判定方法（ SAS,SSS ），猜想可以添加什么条件来判定两个三角形相似？ 3 3 5 5 相似 导入新课 ①任意画 △ ABC ; ② 再画△ A′B′C ′ ，使∠ A ′ =∠ A , 且 ③ 量出 B′C ′ 及 BC 的长，计算 的值，并比较是否三边都对应成比例？ ④量出 ∠ B 与 ∠ B′ 的度数， ∠ B′= ∠ B 吗？由此可推出∠ C′ = ∠ C 吗？为什么？ ⑤由上面的画图，你能发现△ A′B′C ′ 与△ ABC 有何关系？与你周围的同学交流 . 我发现这两个三角形是相似的 相似三角形的判定定理 2 一 画一画 讲授新课 如图，在 △ ABC 与 △ A′B′C ′ 中，已知 ∠ A = ∠ A′ ， 证明：在△ A′B′C ′ 的边 A′B ′ 上截取点 D , 使 A′D=AB ． 过点 D 作 DE ∥ B′C ′, 交 A′C ′ 于点 E . ∵ DE ∥ B′C ′, ∴△ A′DE ∽△ A′B′C ′. 求证：△ A′B′C ′ ∽△ ABC . B A C B' A' D E C' 验证猜想 ∵ A′D=AB ， ∴ A′E = AC. 又∠ A′= ∠ A. ∴△ A′DE ≌ △ ABC ， ∴△ A′B′C′ ∽△ ABC . B A C D E B ' A' C ' 如果△ ABC 与 △A'B'C' 两边成比例，且其中一边 所对的角相等，那么这两个三角形一定相似吗？ 由此你能得到什么结论？ 你有疑问吗 ？ 3 3 C C 60° ) 4 A B ) 【结论】判定两个三角形相似角必须两边的夹角 . C ′ 1.5 B ′ 2 60° A ′ 三角形的判定定理 2 ： 两边成比例且夹角相等的两个三角形相似． 归纳总结 解：∵ AE =1.5 ， AC =2 ， ∴ ∵ ∴ 又∵∠ EAD =∠ CAB , ∴△ ADE ∽△ ABC ( 两边成比例且夹角相等的两个三角形相似 ) ∴ ∴ BC =3. ∴ DE = 例1 : 如图所示， D ， E 分别是△ ABC 的边 AC , AB 上的点， AE =1.5 ， AC =2 ， BC =3 , 且 ，求 DE 的长 . A C B E D 典例精析 例2 : 如图， 在 △ ABC 中 ， C D 是边 AB 上的高，且 　　　　　　　求证： ∠ ACB =90 ° ． A B C D 解： ∵ CD 是边 AB 上的高 , ∴ ∠ ADC = ∠ CDB =90°. ∴ △ ADC ∽ △ C DB . ∴ ∠ ACD = ∠ B . ∴ ∠ ACB = ∠ ACD + ∠ BCD = ∠ B + ∠ BCD = 90°. 1. 如图， D 是 △ ABC 一边 BC 上一点，连接 AD ,使 △ ABC ∽ △ DBA 的条件是 （ ） A . AC : BC=AD : BD B . AC : BC=AB : AD C . AB 2 = CD · BC D . AB 2 = BD · BC D 当堂练习 A B C D 2. 已知在 Rt △ ABC 与 Rt △ A′B′C ′ 中，∠ A =∠ A ′ = 90 ° ， AB =6cm ， AC =4.8cm ， A′B ′ =5cm ， A′C ′ =3cm. 求证：△ A′B′C ′ ∽△ ABC . 证明： ∠ A =∠ A ′ = 90°， ∴△ ABC ∽△ A′B′C ′. 3. △ ABC 为锐角三角形 ， BD、CE 为高 . 求证： △ ADE ∽ △ ABC . 证明： ∵ BD ⊥ AC ， CE ⊥ AB ， ∴∠ ABD +∠ A =90°， ∠ ACE +∠ A = 90°. ∴ ∠ ABD = ∠ ACE . 又 ∵ ∠ A = ∠ A ， ∴△ ABD ∽ △ ACE . ∴ ∵ ∠ A = ∠ A ， ∴ △ ADE ∽ △ ABC . A B D C E O 利用两边及夹角判定三角形相似 定理 2 ：两边对应成比例且夹角相等的两个三角形相似 课堂小结 相似三角形的判定定理 2 的运用