- 2021-05-26 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版八年级下册数学同步练习课件-第1章-4 角平分线(一)
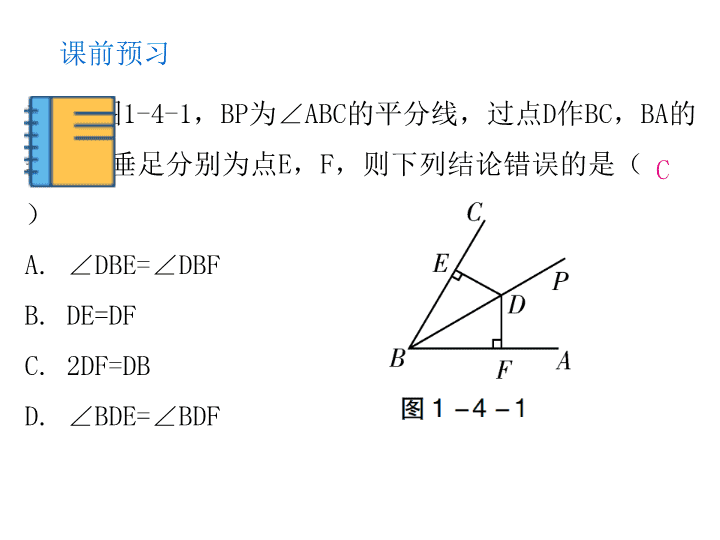
中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 4 角平分线 第一章 三角形的证明 第1课时 角平分线 (一) 1. 如图1-4-1,BP为∠ABC的平分线,过点D作BC,BA的 垂线,垂足分别为点E,F,则下列结论错误的是( ) A. ∠DBE=∠DBF B. DE=DF C. 2DF=DB D. ∠BDE=∠BDF 课前预习 C 2. 如图1-4-2,点P是∠AOB平分线OC上一点,PD⊥OB, 垂足为点D,若PD=2,则点P到边OA的距离是( ) A. 2 B. 3 C. D. 4 A 3. 如图1-4-3,若DE⊥AB,DF⊥AC,则对于∠1和∠2的 大小关系,下列说法正确的是( ) A. 一定相等 B. 一定不相等 C. 当BD=CD时相等 D. 当DE=DF时相等 D 课堂讲练 新知1:角平分线的性质定理 典型例题 【例1】如图1-4-4,AD为△ABC的角平分线,DE⊥AB 于点E,DF⊥AC于点F,EF交AD于点O.求证:OE=OF. 证明:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC, ∴DE=DF. 在Rt△AED和Rt△AFD中, AD=AD, DE=DF, ∴Rt△AED≌Rt△AFD(HL). ∴AE=AF. ∴AD是EF的垂直平分线. ∴OE=OF. 模拟演练 1. 如图1-4-5,AB=AC,BD=CD,DE⊥AB,点E为垂足, DF⊥AC,点F为垂足,求证:DE=DF. AB=AC, 证明:在△ABD和△ACD中, BD=CD, AD=AD, ∴△ABD≌△ACD(SSS). ∴∠BAD=∠CAD. 又∵DE⊥AB,DF⊥AC, ∴DE=DF. 【例2】如图1-4-6,在△ABC中,AD平分∠BAC,DE⊥AB 于点E,DF⊥AC于点F,AB=6,AC=4. 若S△ABD=9,求 S△ACD. 典型例题 解:∵DE⊥AB,DF⊥AC,AD平分∠BAC, ∴DE=DF. ∵S△ABD=9,AB=6, ∴DE=3. ∴DF=3. ∵AC=4, ∴S△ACD= AC·DF=6. 2. 如图1-4-7,在△ABC中,CD是AB边上的高,BE平 分∠ABC,交CD于点E,BC=5,DE=2,求△BCE的面积. 模拟演练 解:如答图1-4-2,过点E作EF⊥BC于点F. ∵CD是AB边上的高, ∴ED⊥AB. ∵BE平分∠ABC, ∴DE=EF=2. ∵BC=5, ∴S△BCE= BC·EF= ×5×2=5. 【例3】如图1-4-8,在△ABC中,点D,E,F在边BC上, 点P在线段AD上.已知PE∥AB,∠PFD=∠C,点D到AB和AC 的距离相等.求证:点D到PE和PF的距离相等. 典型例题 新知2:角平分线性质定理的逆定理 证明:如答图1-4-1,作DM⊥AB于点M,交PE于点G, 作DN⊥AC于点N,交PF于点H. ∵DM⊥AB,DN⊥AC,且DM=DN, ∴∠BAD=∠CAD. ∵PE∥AB, ∴∠EPD=∠BAD,DG⊥PE. ∵∠PFD=∠C,∴PF∥AC. ∴∠FPD=∠CAD,DH⊥DF. ∴∠EPD=∠FPD. ∴DG=DH,即点D到PE和PF的距离相等. 3. 如图1-4-9,BD⊥AM于点D,CE⊥AN于点E,BD,CE相 交于点F,CF=BF. 求证:点F在∠A的平分线上. 模拟演练 证明:如答图1-4-3,连接AF. ∵BD⊥AM,CE⊥AN, ∴∠FDC=∠FEB=90°. 又∵∠CFD=∠BFE,CF=BF, ∴△CDF≌△BEF(AAS). ∴FD=FE. ∵BD⊥AM,CE⊥AN, ∴∠CAF=∠BAF. ∴AF平分∠BAC,即点F在∠A的平分线上. 分层训练 A组 1. 如图1-4-10,在CD上求一点P,使它到OA,OB的距 离相等,则点P是( ) A. 线段CD的中点 B. OA与OB的中垂线的交点 C. OA与CD的中垂线的交点 D. CD与∠AOB的平分线的交点 D 2. 如图1-4-11,OP是∠AOB的平分线,点P到OA的距离 PE为3,点N是OB上的任意一点,则线段PN的取值范围为 ( ) A. PN<3 B. PN>3 C. PN≥3 D. PN≤3 C 3. 如图1-4-12,在Rt△ABC中,∠C=90°,AD是△ABC 的角平分线. 若CD=4,AC=12,AB=15,则△ABC的面积 为( ) A. 48 B. 50 C. 54 D. 60 C 4. 如图1-4-13,在△ABC中,AD是角平分线,DE⊥AB于 点E,△ABC的面积为15,AB=6,DE=3,则AC的长是 ( ) A. 8 B. 6 C. 5 D. 4 D B组 5. 如图1-4-14,点A,B分别是∠NOP,∠MOP平分线上 的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则 下列结论错误的是( ) A. AD+BC=AB B. ∠AOB=90° C. 与∠CBO互余的角有2个 D. 点O是CD的中点 C 6. 如图1-4-15,AB=AC,BE⊥AC于点E,CF⊥AB于点F, BE,CF交于点D,则以下结论:①△ABE≌△ACF; ②△BDF≌△CDE;③点D在∠BAC的平分线上,正确的是 ( ) A. ① B. ② C. ①② D. ①②③ D 7. 已知:如图1-4-16,OC是∠AOB的平分线,P是OC上 的一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,点F是 OC上的另一点,连接DF,EF. 求证:DF=EF. 证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB, ∴PD=PE. 在Rt△OPD和Rt△OPE中, OP=OP, PD=PE, ∴Rt△OPD≌Rt△OPE(HL). ∴OD=OE. ∵OC是∠AOB的平分线,∴∠DOF=∠EOF. OD=OE, 在△ODF和△OEF中,∠DOF=∠EOF, OF=OF, ∴△ODF≌△OEF(SAS). ∴DF=EF. 8. 如图1-4-17,在Rt△ABC中,∠ACB=90°,BD是 △ABC的角平分线. 点O是BD上一点,过点O分别作AC, B C 的 垂 线 , 垂 足 分 别 为 点 F , E , 连 接 O C , O A , ∠FCO=45°.求证:点O在∠BAC的平分线上. 证明:如答图1-4-4,过点O作OH⊥AB于点H. ∵BD是△ABC的角平分线,OE⊥BC,OH⊥AB, ∴OE=OH. ∵∠ACB=90°,∠FCO=45°, ∴CO平分∠ACB. ∵OE⊥BC,OF⊥AC, ∴OE=OF. ∴OF=OH. ∴点O在∠BAC的平分线上. C组 9. 如图1-4-18,在△ABC中,∠C=90°,AD是∠BAC的平 分线,DE⊥AB于点E,点F在AC上,BD=DF. 求证: (1)CF=EB; (2)AB=AF+2EB. 证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC, ∴DE=DC. 在Rt△DCF和Rt△DEB中, DF=DB, DC=DE, ∴Rt△DCF≌Rt△DEB(HL). ∴CF=EB. (2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC, ∴CD=ED. 在△ADC和△ADE中, AD=AD, CD=ED, ∴△ADC≌△ADE(HL). ∴AC=AE. ∴AB=AE+EB=AC+EB=AF+CF+EB=AF+2EB.查看更多