- 2021-05-26 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
苏教版八年级数学上册期中考试过关测试卷
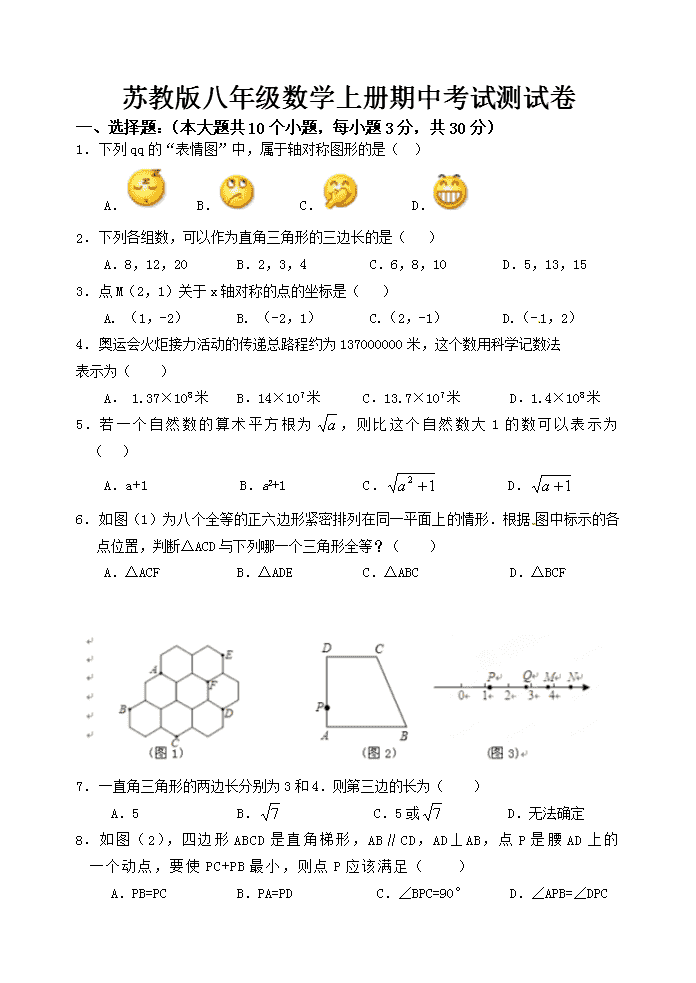
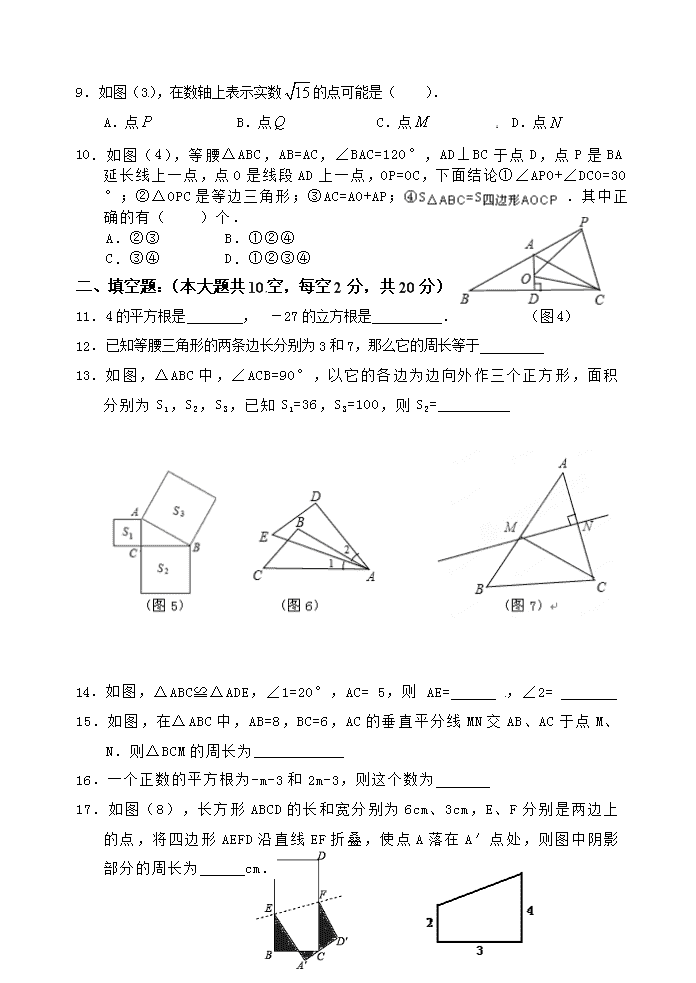
苏教版八年级数学上册期中考试测试卷 一、选择题:(本大题共 10 个小题,每小题 3 分,共 30 分) 1.下列 qq 的“表情图”中,属于轴对称图形的是( ) A. B. C. D. 2.下列各组数,可以作为直角三角形的三边长的是( ) A.8,12,20 B.2,3,4 C.6,8,10 D.5,13,15 3.点 M(2,1)关于 x 轴对称的点的坐标是( ) A. (1,-2) B. (-2,1) C.(2,-1) D.(-1,2) 4.奥运会火炬接力活动的传递总路程约为 137000000 米,这个数用科学记数法 表示为( ) A. 1.37×108 米 B.14×107 米 C.13.7×107 米 D.1.4×108 米 5. 若 一 个 自 然 数 的 算 术 平 方 根 为 a , 则 比 这 个 自 然 数 大 1 的 数 可 以 表 示 为 ( ) A.a+1 B.a2+1 C. 12 a D. 1a 6. 如图(1)为八个全等的正六边形紧密排列在同一平面上的情形.根据 图中标示的各 点位置,判断△ACD 与下列哪一个三角形全等?( ) A.△ACF B.△ADE C.△ABC D.△BCF 7.一直角三角形的两边长分别为 3 和 4.则第三边的长为( ) A.5 B. 7 C.5 或 7 D.无法确定 8.如图(2),四边形 ABCD 是直角梯形 ,AB∥CD,AD⊥AB,点 P 是腰 AD 上的一 个动点,要使 PC+PB 最小,则点 P 应该满足( ) A.PB=PC B.PA=PD C.∠BPC=90° D.∠APB=∠DPC 9.如图(3),在数轴上表示实数 15 的点可能是( ). A.点 P B.点 Q C.点 M D.点 N 10. 如 图 ( 4), 等 腰 △ ABC, AB=AC, ∠ BAC=120° , AD⊥ BC 于 点 D, 点 P 是 BA 延长线上一点,点 O 是线段 AD 上一点,OP=OC,下面结论①∠APO+∠DCO=30°; ②△OPC 是等边三角形;③AC=AO+AP; .其中正确的 有( )个. A.②③ B.①②④ C.③④ D.①②③④ 二、填空题:(本大题共 10空,每空 2 分,共 20 分) 11.4 的平方根是 , -27 的立方根是 . (图 4) 12.已知等腰三角形的两条边长分别为 3 和 7,那么它的周长等于 13. 如 图 , △ ABC 中 , ∠ ACB=90° , 以 它 的 各 边 为 边 向 外 作 三 个 正 方 形 , 面 积 分别为 S1,S2 ,S3,已知 S1=36,S3=100,则 S2= 14.如图,△ABC≌△ADE,∠1=20°,AC= 5,则 AE= ,∠2= 15.如图,在△ABC 中,AB=8,BC=6,AC 的垂直平分线 MN 交 AB、AC 于点 M、N.则 △BCM 的周长为 16.一个正数的平方根为-m-3 和 2m-3,则这个数为 17.如图(8),长方形 ABCD 的长和宽分别为 6cm、3cm,E、F 分别是两边上的 点,将四边形 AEFD 沿直线 EF 折叠,使点 A 落在 A′点处,则图中阴影部分 的周长为 cm. (图 8) (图 9) 18.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去 两个三角形,剩下的部分是如图(9)所示的直角梯形,其中三边长分别为 2、3、4,则 原直角三角形纸片的斜边长是 三、解答题:(本大题共 7 小题,共 50 分) 19.计算:(每题 3 分,共 6 分) (1) 1684 3 (2)|1- 2|+(1- 2)0 + (-2)2 20.( 本题 满分 5 分) 已知 2x-y 的平方根为± 4,-2 是 y 的立方根,求-2xy 的 平方根. 21.(本 题满 分 5 分) 如图所示 ,四边形 ABCD 中,AB=3cm,AD=4cm,BC=13cm, CD=12cm,∠A=90°,求四边形 ABCD 的面积. 22.(本 题满分 4 分) 两两相交的三条公路经过 A、B、C 三个村庄. (1)要建一个水电站 P 到三个村庄的距离相等,请通过画图确定点 P 的位置. (2)要建一个加油站 Q,使加油站 Q 到三条公路的距离相等,这样的加油站 Q 的位置 有_ _处. 23.(本 题满 分 6 分) 已知:如图,点 A,E,F,C 在同一条直线上,AD=CB, ∠B=∠D,AD∥BC.求证:AE=CF. 24.( 本题满 分 6 分) 11 世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题 “小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是 30 肘尺(肘尺是古代的长 度单位),另外一棵高 20 肘尺;两棵棕榈树的树干间的距离是 50 肘尺.每棵树的树顶 上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞 去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多 远? C B A 25.(本题 满分 9 分).问题背景 在△ABC 中,∠B=2∠C,点 D 为线段 BC 上 一动点,当 AD 满足某种条件时,探讨在线段 AB、BD、CD、AC 四条线段中, 某两条或某三条线段之间存在的数量关系. 在图 1 中, 当 AB=AD 时, 则可得 AB=CD,请你 给出证 明过程 。 现在继续探索: 任务要求: (1)当 AD⊥BC 时,如图 2,求证:AB+BD=DC; (2)当 AD 是∠BAC 的角平分线时,判断 AB、BD、AC 的数量关系,并证明 你的结 26.( 本题 满分 9 分 )如图,△ABC 是边长为 6 的等边三角形,P 是 AC 边的一动点,由 A 向 C 运动(与 A、C 不重合),Q 是 CB 延长线上一动点,与点 P 同时以相同的速度由 B 向 CB 延长线方向运动(Q 不与 B 重合),过 P 作 PE⊥AB 于 E,连接 PQ 交 AB 于 D. (1)当∠BQD=30°时,求 AP 的长; (2)在运动过程中线段 ED 的长是否发生变化?如果不变,求出线段 ED 的长;如果发 生改变,请说明理由.查看更多