中考数学一轮复习知识点+题型专题讲义17 三角形与多边形(教师版)
专题 17 三角形与多边形
考点总结
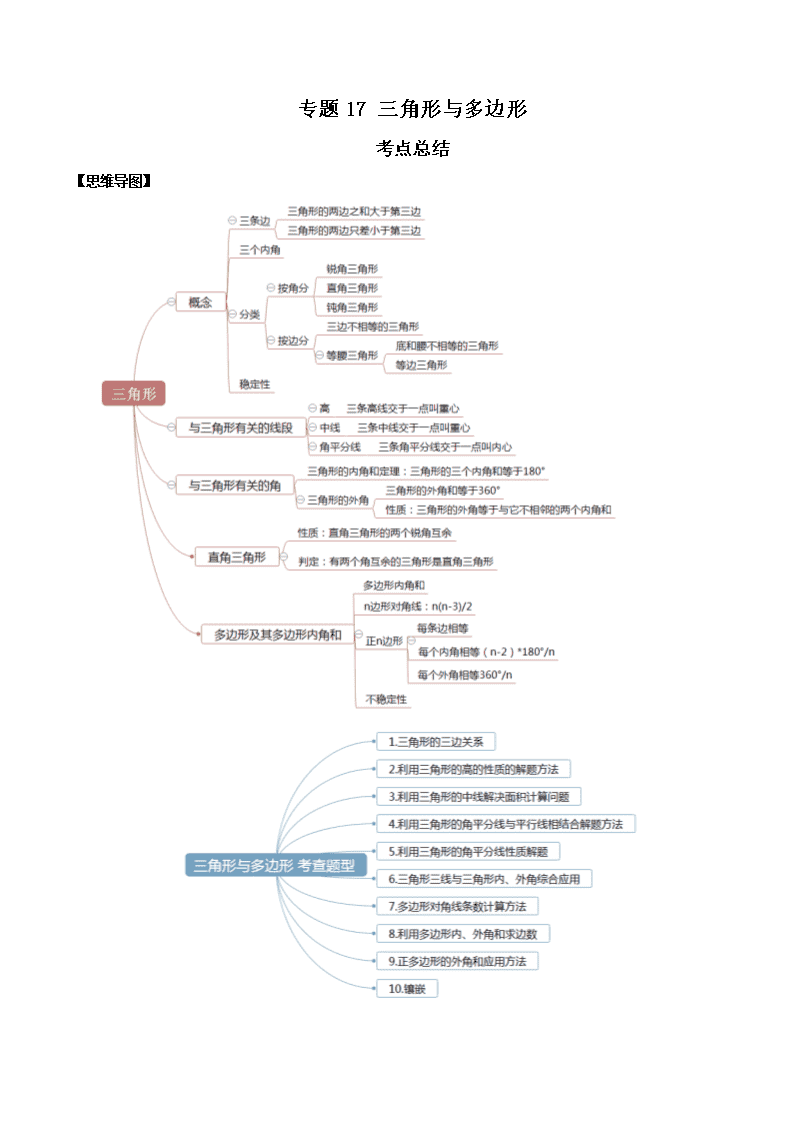
【思维导图】
【知识要点】
知识点一 三角形的概念
三角形的概念 :由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
三角形特性
(1)三角形有三条线段
(2)三条线段不在同一直线上 三角形是封闭图形
(3)首尾顺次相接
三角形用符号“ ”表示,顶点是 A、B、C 的三角形记作“ ABC”,读作“三角形 ABC”。
三角形按边分类 :
等腰三角形:有两条边相等的三角形叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底边,两腰
的夹角叫做顶角,腰与底边的夹角叫做底角。
等边三角形:底边与腰相等的等腰三角形叫做等边三角形,即三边都相等。
三角形三边的关系(重点)
(1)三角形的任意两边之和大于第三边。
三角形的任意两边之差小于第三边。(这两个条件满足其中一个即可)
用数学表达式表达就是:记三角形三边长分别是 a,b,c,则 a+b>c 或 c-b<a。
(2) 已知三角形两边的长度分别为 a,b,求第三边长度的范围:|a-b|<c<a+b
考查题型一 三角形的三边关系
1.(2018·湖南中考真题)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm B.8cm,8cm,15cm C.5cm,5cm,10cm D.6cm,7cm,14cm
【答案】B
【解析】
详解:A、∵5+4=9,9=9,
∴该三边不能组成三角形,故此选项错误;
B、8+8=16,16>15,
∴该三边能组成三角形,故此选项正确;
C、5+5=10,10=10,
∴该三边不能组成三角形,故此选项错误;
D、6+7=13,13<14,
∴该三边不能组成三角形,故此选项错误;
故选:B.
2.(2018·湖南中考真题)已知三角形两边的长分别是 3 和 7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
【答案】C
【解析】设第三边长为 x,则有
7-3
2,
符合三角形三边关系,此时周长是 12 cm.故选 B.
三角形的稳定性
三角形具有稳定性
四边形及多边形不具有稳定性
要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了。
1.(2011·四川中考真题)王师傅用 4 根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还
要再钉上几根木条?( ).
A.0 根 B.1 根 C.2 根 D.3 根
【答案】B
【解析】
三角形具有稳定性,连接一条对角线,即可得到两个三角形,故选 B
2.(2019·山东中考模拟)下列图形中具有稳定性的是( )
A.正方形 B.长方形 C.等腰三角形 D.平行四边形
【答案】C
【解析】
解:根据“三角形具有稳定性”可知等腰三角形有稳定性.
故 C 项符合题意.
故本题正确答案为 C.
3.(2019·福建厦门一中中考模拟)下列图形具有稳定性的是( )
A. B. C. D.
【答案】A
【解析】A、具有稳定性,符合题意;
B、不具有稳定性,故不符合题意;
C、不具有稳定性,故不符合题意;
D、不具有稳定性,故不符合题意,
故选 A.
知识点二 与三角形有关的线段
三角形的高概念:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形
的高)。
考查题型二 利用三角形的高的性质的解题方法
1.(2017·安徽芦集初级中学中考模拟)如图,AD,CE 是△ABC 的两条高,已知 AD=10,CE=9,AB=12,
则 BC 的长是( )
A.10 B.10.8 C.12 D.15
【答案】B
【解析】
∵AD,CE 是△ABC 的两条高,AD=10,CE=9,AB=12,
∴△ABC 的面积= 1
2 ×12×9= 1
2 BC⋅AD=54,
即 12BC⋅10=54,解得 BC=10.8.
故选:B.
2.(2013·江苏中考模拟)如图,四边形 ABCD 的对角线 AC 和 BD 相交于点 E,如果△CDE 的面积为 3,
△BCE 的面积为 4,△AED 的面积为 6,那么△ABE 的面积为( )
A.7 B.8 C.9 D.10
【答案】B
【解析】
试题分析:△CDE 与△AED 的同底,底为 DE;△BCE 与△ABE 的底相同,为 BE,△CDE 与△BCE 在
DE、BE 上高相同;△AED 与△ABE 在 DE、BE 上高相同,
��th
��th �
��晦h
��晦h
,解得
��晦h
=8
3.(2019·沭阳县修远中学中考模拟)如图,△ABC 中,AD 是 BC 边上的高,AE 是∠BAC 的平分线,∠EAD
=5°,∠B=50°,求∠C 的度数.
【答案】60°.
【解析】
∵AD 是 BC 边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED-∠B=85°-50°=35°,
∵AE 是∠BAC 的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
三角形的中线概念:在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。
性质:三角形三条中线的交于一点,这一点叫做“三角形的重心”。三角形的中线可以将三角形分为面积相
等的两个小三角形。
考查题型三 利用三角形的中线解决面积计算问题
1.(2011·湖北中考真题)如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,
△ADF,△BEF 的面积分别为 S△ABC,S△ADF,S△BEF,且 S△ABC=12,则 S△ADF-S△BEF=( )
A.1 B.2 C.3 D.4
【答案】B
【解析】
∵S△ABC=12,
EC=2BE,点 D 是 AC 的中点,
∴S△ABE= 1
3 ×12=4,
S△ABD= 1
2 ×12=6,
∴S△ABD-S△ABE,
=S△ADF-S△BEF,
=6-4,
=2.
故选 B.
2.(2018·江苏省无锡金桥双语实验学校中考模拟)如图,在△ABC 中,已知 D,E 分别为边 BC,AD 的中
点,且 S△ABC=4 cm2,则△BEC 的面积为( )
A.2 cm2 B.1 cm2 C.0.5 cm2 D.0.25 cm2
【答案】A
【解析】
∵E 为 AD 的中点,
∴BE、CE 分别是△ABD、△ACD 的中线,
∴S△BDE= 1
2 S△ABD,S△CDE= 1
2 S△ACD,
∴S△BEC= 1
2 S△ABC= 1
2 ×4=2(cm2),
即 S△BEC 的值为 2 cm2.
故选:A.
3.(2017·安徽芦集初级中学中考模拟)如图,AD 为△ABC 的中线,BE 为△ABD 的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED 的度数;
(2)作图:在△BED 中作出 BD 边上的高 EF;BE 边上的高 DG;
(3)若△ABC 的面积为 40,BD=5,则△BDE 中 BD 边上的高 EF 为多少?若 BE=6,求△BED 中 BE 边上的
高 DG 为多少?
【答案】(1)∠BED=55°;(2)画图见解析;(3)EF=4,DG=10
3 .
【解析】
(1)∵∠BED 是△ABE 的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)画图如下:
(3)∵AD 为△ABC 的中线,BE 为△ABD 的中线,
∴△ABD 的面积= 1
2
△ABC 的面积=20,△BDE 的面积= 1
2
△ABD 的面积=10,
∴ 1
2 BD·EF=10, 1
2 ×5EF=10,
解得 EF=4,
1
2 BE·DG=10, 1
2 ×6 DG =10,
EF=10
3 .
三角形的角平分线概念:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角
形的角平分线。
注意:三角形的角平分线是一条线段,角的平分线是一条射线。
考查题型四 利用三角形的角平分线与平行线相结合解题方法
1.(2019·开封市第五中学初二期中)在△ABC 中,CD 平分∠ACB 交 AB 于点 D,过点 D 作 DE∥BC,交
AC 于点 E.若∠A=46°,∠B=54°,求∠CDE 的度数.
【答案】40°.
【解析】
解∵在△ABC 中,∠A=46°,∠B=54°,
∴∠ACB=80°,
又∵CD 平分∠ACB,
∴∠BCD=40°,
又∵ED∥BC,
∴∠CDE =∠BCD=40°.
答:∠CDE 的度数 40°.
2.如图,在△ABC 中,CD 平分∠ACB 交 AB 于点 D,E 为 AC 上一点,且 DE∥BC
(1)求证:DE=CE;
(2)若∠A=90°,S△BCD=26,BC=13,求 AD.
【答案】(1)详见解析;(2)4.
【解析】
解:(1)∵CD 平分∠ACB,∴∠ECD=∠BCD,又∵DE∥BC ∴∠BCD=∠CDE.
∴∠ECD=∠EDC ∴DE=CE;
(2)如图,过 D 作 DF⊥BC 于 F,
∵∠A=90°,CD 平分∠ACB,∴AD=FD,
∵S△BCD=26,BC=13,∴ 1
2 ×13×DF=26,∴DF=4,∴AD=4.
3.(2019·邛崃市西桥九年制学校初一期中)如图,在三角形 ABC 中,CD 平分∠ACB,DE∥BC,∠AED
=80°,求∠EDC 的度数.
【答案】∠EDC=40°
【解析】
解:∵DE∥BC,∠AED=80°,
∴∠ACB=∠AED=80°,
∵CD 平分∠ACB,
∴∠BCD= 1
2
∠ACB=40°,
∵DE∥BC,
∴∠EDC=∠BCD=40°.
考查题型五 利用三角形的角平分线性质解题
1.(2017·湖北中考模拟)如图,直线 AB,CD 相交于点 O,射线 OM 平分∠AOC,ON⊥OM,若∠AOM
=35°,则∠CON 的度数为( )
A.35° B.45° C.55° D.65°
【答案】C
【解析】
解:∵射线 OM 平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
故选 C.
2.(2018·四川中考模拟)如图,在△ABC 中,AD 是 BC 边上的高,BE 平分∠ABC 交 AC 边于 E,∠BAC=60°,
∠ABE=25°,则∠DAC 的大小是( )
A.15° B.30° C.25° D.20°
【答案】D
【解析】
试题解析: 2 2 25 50ABC ABE ,
∵AD 是 BC 边上的高,
90 90 50 40BAD ABC ,
60 40 20 .DAC BAC BAD
故选 D.
3.(2019·安徽中考模拟)如图,点 O 在△ABC 内,且到三边的距离相等.若∠BOC=120°,则 tanA 的值
为( )
A. 3 B. 3
3
C. 3
2
D. 2
2
【答案】A
【解析】
解:∵点 O 到△ABC 三边的距离相等,
∴BO 平分∠ABC,CO 平分∠ACB,
∴∠A=180°﹣(∠ABC+∠ACB)
=180°﹣2(∠OBC+∠OCB)
=180°﹣2×(180°-120°)
=180°﹣2×60°=60°,
∴tanA=tan60°= 3 ,
故选 A.
知识点三 与三角形有关的角
三角形的内角和定理:三角形三个内角和等于 180°。
推论:
①直角三角形的两个锐角互余。
②三角形的一个外角等于和它不相邻的来两个内角的和。
③三角形的一个外角大于任何一个和它不相邻的内角。
备注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。等角的补角相等,等角
的余角相等。
1.(2017·湖南中考真题)一个三角形三个内角的度数之比为 1:2:3,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
【答案】B
【解析】
根据三角形的内角和为 180°,可知最大角为 90°,因式这个三角形是直角三角形.
故选:B.
2.(2013·福建中考真题)在△ABC 中,∠A=20°,∠B=60°,则△ABC 的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
【答案】D
【解析】
解:∵∠A=20°,∠B=60°,
∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°,
∴△ABC 是钝角三角形.
故选 D.
3.(2013·湖南中考真题)如图,在 Rt△ACB 中,∠ACB=90°,∠A=25°,D 是 AB 上一点.将 Rt△ABC
沿 CD 折叠,使 B 点落在 AC 边上的 B′处,则∠ADB′等于( )
A.25° B.30° C.35° D.40°
【答案】D
【解析】
∵在 Rt△ACB 中,∠ACB=90°,∠A=25°,∴∠B=90°﹣25°=65°。
∵△CDB′由△CDB 反折而成,∴∠CB′D=∠B=65°。
∵∠CB′D 是△AB′D 的外角,∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°。
故选 D。
4.(2019·海口市灵山中学中考模拟)已知△ABC 的三个内角∠A,∠B,∠C 满足关系式∠B+∠C=3∠A,
则此三角形( )
A.一定有一个内角为 45° B.一定有一个内角为 60°
C.一定是直角三角形 D.一定是钝角三角形
【答案】A
【解析】
解:∵∠B+∠C+∠A=180°,∠B+∠C=3∠A,
∴∠B+∠C+∠A=4∠A=180°,
∴∠A=45°.
故选:A.
5.(2019·新疆中考模拟)如图,AB∥CD,点 E 在线段 BC 上,CD=CE,若∠ABC=30°,则∠D 为( )
A.85° B.75° C.60° D.30°
【答案】B
【解析】
∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即 30°+2∠D=180°,
∴∠D=75°.
故选 B.
6.(2013·河北中考真题)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2 等于( )
A.90° B.100° C.130° D.180°
【答案】B
【解析】
如图,∠1=90°-∠BAC;
∠2=120°-∠ACB;
∠3=120°-∠ABC;
∴∠1+∠2+∠3=90°-∠BAC+120°-∠ACB+120°-∠ABC=150°
∵∠3=50°
∴∠1+∠2=100°
故选 B
7.(2012·山东中考真题)如图所示,B 处在 A 处的南偏西 45°方向,C 处在 A 处的南偏东 15°方向,C 处在
B 处的北偏东 80°方向,则∠ACB 等于( )
A.40° B.75° C.85° D.140°
【答案】C
【解析】
∵AE,DB 是正南正北方向,
∴BD∥AE,
∵∠DBA=45°,
∴∠BAE=∠DBA=45°,
∵∠EAC=15°,
∴∠BAC=∠BAE+∠EAC=45°+15°=60°,
又∵∠DBC=80°,
∴∠ABC=80°-45°=35°,
∴∠ACB=180°-∠ABC-∠BAC=180°-60°-35°=85°
故选 C
三角形的外角和定理:三角形的一边与另一边的延长线组成的角叫做三角形的外角
性质:1.三角形的一个外角等于与它不相邻的两个内角之和。
2.三角形的一个外角大于与它不相邻的任何一个内角。
1.(2018·内蒙古中考模拟)将一副三角板按图中方式叠放,则角α等于( )
A.30° B.45° C.60° D.75°
【答案】D
【解析】
如图,根据两直线平行,内错角相等,
∴∠1=45°,
根据三角形的一个外角等于与它不相邻的两个内角的和,
∴∠α=∠1+30°=75°.
故选 D.
2.(2018·山东中考模拟)如图,已知 a//b, ∠1=120°, ∠2=90°,则∠3 的度数是( )
A.120° B.130° C.140° D.150°
【答案】D
【解析】
如图,延长 1 的边与直线b 相交,
/ /a b ,
4 180 1 180 120 60 ,
由三角形的外角性质可得,
3 90 4 90 60 150 .
故选: D .
3.(2013·湖南中考真题)如图,一副分别含有 30°和 45°角的两个直角三角板,拼成如下图形,其中∠C=90°,
∠B=45°,∠E=30°,则∠BFD 的度数是( )
A.15° B.25° C.30° D.10°
【答案】A
【解析】
∵Rt△CDE 中,∠C=90°,∠E=30°,
∴∠BDF=∠C+∠E=90°+30°=120°
∵△BDF 中,∠B=45°,∠BDF=120°,
∴∠BFD=180°﹣45°﹣120°=15°.
故选 A.
4.(2018·广西中考真题)如图,∠ACD 是△ABC 的外角,CE 平分∠ACD,若∠A=60°,∠B=40°,则∠ECD
等于( )
A.40° B.45° C.50° D.55°
【答案】C
【解析】∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°,
∵CE 平分∠ACD,
∴∠ECD= 1
2
∠ACD=50°,
故选 C.
5.(2019·广西中考模拟)小桐把一副直角三角尺按如图所示的方式摆放在一起,其中 90E , 90C ,
45A , 30D ,则 1 2 等于 ( )
A.150 B.180 C. 210 D. 270
【答案】C
【解析】
如图:
1 D DOA , 2 E EPB ,
DOA COP , EPB CPO ,
∴ 1 2 D E COP CPO
= D E 180 C
=30 90 180 90 210 ,
故选 C.
6.(2019·贵州中考模拟)如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120° B.130° C.140° D.150°
【答案】C
【解析】
如图,延长 AC 交 EF 于点 G;∵AB∥EF,∴∠DGC=∠BAC=50°;
∵CD⊥EF,∴∠CDG=90°,∴∠ACD=90°+50°=140°,故选 C.
考查题型六 三角形三线与三角形内、外角综合应用
1.(2019·湖南中考模拟)如图,∠ABC=38°,∠ACB=100°,AD 平分∠BAC,AE 是 BC 边上的高,求∠DAE
的度数.
【答案】 31 .DAE
【解析】
∵∠ABC=38°,∠ACB=100°(己知)
∴∠BAC=180°―38°―100°=42°(三角形内角和 180°)
又∵AD 平分∠BAC(己知) ∴∠BAD=21°
∴∠ADE=∠ABC+∠BAD=59°(三角形的外角性质)
又∵AE 是 BC 边上的高, 即∠E=90°
∴∠DAE=90°―59°=31°
2.(2019·湖南中考模拟)已知如图在△ABC 中,∠ABC 平分线与∠ACE 的外角平分线相交于点 P.若
∠A=70°,求∠P 的度数.
【答案】∠P=35°
【解析】
如图;
∵BP 平分∠ABC,PC 平分∠ACE
∴∠ABP=∠CBP= 1
2
∠ABC,∠ACP=∠ECP= 1
2
∠ACE
∵∠A=70°,
∴∠ACE=70°+∠ABC
同理∠PCE=∠P+∠PBC,
∴2(∠P+∠PBC)=∠A+∠ABC=∠A+2∠PBC
∴∠P= 1
2
∠A= 1
2 ×70°=35°
3.(2019·新宁县第二中学中考模拟)如图所示,在△ABC 中,BO、CO 是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC 的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC 的度数.
(3)若∠A=n°,求∠BOC 的度数.
【答案】(1)125°;(2)125°;(3)∠BOC=90°+
�
�
n°.
【解析】
如图,
∵BO、CO 是角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
∵∠ABC+∠ACB+∠A=180°,
∴2∠1+2∠2+∠A=180°,
∵∠1+∠2+∠BOC=180°,
∴2∠1+2∠2+2∠BOC=360°,
∴2∠BOC﹣∠A=180°,
∴∠BOC=90°+
�
�
∠A,
(1)∵∠ABC=50°,∠ACB=60°,
∴∠A=180°﹣50°﹣60°=70°,
∴∠BOC=90°+
�
�
×70°=125°;
(2)∠BOC=90°+
�
�
∠A=125°;
(3)∠BOC=90°+
�
�
n°.
知识点四 多边形及其多边形内角和
多边形的相关知识:
在平面中,由一些线段首尾顺次相接组成的图形叫做多边形,多边形中相邻两边组成的角叫做它的内
角。多边形的边与它邻边的延长线组成的角叫做外角。
连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
一个 n 边形从一个顶点出发的对角线的条数为(n-3)条,其所有的对角线条数为
2
)3( nn
凸多边形 :画出多边形的任何一条边所在的直线,如果多边形的其它边都在这条直线的同侧,那么这个多
边形就是凸多边形。
正多边形 :各角相等,各边相等的多边形叫做正多边形。(两个条件缺一不可,除了三角形以外,因为若三
角形的三内角相等,则必有三边相等,反过来也成立)
多边形的内角和
n 边形的内角和定理:n 边形的内角和为(n−2)∙180°
n 边形的外角和定理:多边形的外角和等于 360°,与多边形的形状和边数无关。
考查题型七 多边形对角线条数计算方法
1.(2018·河北中考模拟)连接多边形任意两个不相邻顶点的线段称为多边形的对角线.
(1)
对角线条数分别为 、 、 、 .
(2)n 边形可以有 20 条对角线吗?如果可以,求边数 n 的值;如果不可以,请说明理由.
(3)若一个 n 边形的内角和为 1800°,求它对角线的条数.
【答案】(1)2;5;9; ( 3)
2
n n ;(2)n 边形可以有 20 条对角线,此时边数 n 为八;(3)这个多边形有
54 条对角线
【解析】
(1)设 n 边形的对角线条数为 an,
则 a4= 4 4 3
2
=2,a5= 5 5 3
2
=5,a6= 6 6 3
2
=9,…,an= 3
2
n n .
(2)假设可以,根据题意得:
3
2
n n =20,
解得:n=8 或 n=-5(舍去),
∴n 边形可以有 20 条对角线,此时边数 n 为八.
(3)∵一个 n 边形的内角和为 1800°,
∴180°×(n-2)=1800°,
解得:n=12,
∴ 3
2
n n = 12 12 3
2
=54.
答:这个多边形有 54 条对角线.
2.(2018·河北中考模拟)已知 n 边形的对角线共有 ( 3)
2
n n 条(n 是不小于 3 的整数);
(1)五边形的对角线共有_____条;
(2)若 n 边形的对角线共有 35 条,求边数 n;
(3)若 n 边形的边数增加 1,对角线总数增加 9,求边数 n.
【答案】(1)5;(2)10; (3)10.
【解析】
试题分析:(1)把 n=5 代入 3
2
n n ( )即可求得五边形的对角线的条数;
(2)根据题意得 3
2
n n ( )
=35 求得 n 值即可;
(3) 1 1 3
2
n n ( )( )﹣ 3
2
n n ( )
=9,求得 n 的值即可.
试题解析:解:(1)当 n=5 时, 3
2
n n ( )
= 5 2
2
=5.故答案为:5.
(2) 3
2
n n ( )
=35,整理得:n2﹣3n﹣70=0,解得:n=10 或 n=﹣7(舍去),所以边数 n=10.
(3)根据题意得: 1 1 3
2
n n ( )( )﹣ 3
2
n n ( )
=9,解得:n=10.
所以边数 n=10.
考查题型八 利用多边形内、外角和求边数
1.(2019·广东中考模拟)如果 n 边形每一个内角等于与它相邻外角的 2 倍,则 n 的值是( )
A.4 B.5 C.6 D.7
【答案】C
【解析】
解:设外角为 x,则相邻的内角为 2x,
由题意得,2x+x=180°,
解得,x=60°,
360÷60°=6,
故选 C.
2.(2018·辽宁中考模拟)一个多边形内角和是外角和的 2 倍,它是( )
A.五边形 B.六边形 C.七边形 D.八边形
【答案】B
【解析】
设这个多边形是 n 边形,根据题意得:
(n﹣2)×180°=2×360°
解得:n=6.
故选 B.
3.(2019·广东可园中学中考模拟)一个多边形的每个外角都等于 30°,则这个多边形是_____边形。
【答案】12
【解析】
解:360°÷30°=12.
故答案为 12.
4.(2017·安徽芦集初级中学中考模拟)一个多边形,它的内角和比外角和的 4 倍多 180°,求这个多边形的
边数及内角和度数.
【答案】这个多边形的边数是 11,内角和度数是 1620 度.
【解析】
根据题意,得:(n﹣2)•180=1620,
解得:n=11.则这个多边形的边数是 11,
内角和度数是 1620 度.
考查题型九 正多边形的外角和应用方法
1.(2019·青海中考真题)如图所示,小华从 A 点出发,沿直线前进 10 米后左转 20 ,再沿直线前进 10 米,
又向左转 20 ,,照这样走下去,他第一次回到出发地 A 点时,一共走的路程是( )
A.200 米 B.180 米 C.160 米 D.140 米
【答案】B
【解析】
∵多边形的外角和为 360°,而每一个外角为 20°,
∴多边形的边数为 360°÷20°=18,
∴小华一共走了:18×10=180 米.
故选 B.
2.(2019·山东中考模拟)如图,李明从 A 点出发沿直线前进 5 米到达 B 点后向左旋转的角度为α,再沿直
线前进 5 米,到达点 C 后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了 45 米,
则每次旋转的角度α为_____.
【答案】 40.
【解析】
连续左转后形成的正多边形边数为: 45 5 9 ,
则左转的角度是360 9 40 .
故答案是: 40.
考查题型十 镶嵌
1.(2018·湖南中考模拟)学校阅览室在装修过程中,准备用边长相等的正方形和正三角形两种地砖铺满地
面,在每个顶点周围正方形、正三角形地砖的块数可以是( )
A.正方形 2 块,正三角形 2 块 B.正方形 2 块,正三角形 3 块
C.正方形 l 块,正三角形 2 块 D.正方形 2 块,正三角形 l 块
【答案】B
【解析】
正三角形的每个内角是 60°,正方形的每个内角是 90°,
∵3×60°+2×90°=360°,
∴需要正方形 2 块,正三角形 3 块.
故选:B.
2.(2019·巴中市第二中学中考模拟)能铺满地面的正多边形的组合是( )
A.正五边形和正方形 B.正六边形和正方形
C.正八边形和正方形 D.正十边形和正方形
【答案】C
【解析】
正五边形每个内角是180 360 5 108 ,正方形的每个内角是90 ,108 90 360m n , 64 5n m ,
显然 m 取任何正整数时, n 不能得正整数,故不能铺满;
正方形的每个内角是90 ,正六边形的每个内角是120,90 120 360m n , 44 3m n ,显然 n 取任
何正整数时, m 不能得正整数,故不能铺满;
正方形的每个内角是90 ,正八边形的每个内角为:180 360 8 135 , 90 2 135 360 ,
正八边形和正方形能铺满.
故选:C .
3.(2019·平昌县金山中学中考模拟)一幅美丽的图案是由四个边长相等的正多边形镶嵌而成,其中的三个
分别为正三角形、正四边形、正六边形,那么另外一个为( )
A.正三角形 B.正四边形
C.正五边形 D.正六边形
【答案】B
【解析】
∵正三角形、正四边形、正六边形的内角分别为 60°、90°、120°,
又∵360°-60°-90°-120°=90°,
∴另一个为正四边形,
故选 B.
4.(2019·沈阳沈东初级中学中考模拟)下列形状的地砖中,不能把地面作既无缝隙又不重叠覆盖的地砖是
( )
A.正三角形 B.正方形 C.正五边形 D.长方形
【答案】C
【解析】
A、正三角形的每个内角是 60°,能整除 360°,能密铺;
B、正方形的每个内角是 90°,4 个能密铺;
C、正五边形每个内角是 180°-360°÷5=108°,不能整除 360°,不能密铺;
D、长方形的每个内角是 90°,4 个能密铺.
故选 C.
5.(2019·河南中考模拟)用一批相同的正多边形地砖辅地,要求顶点聚在一起,且砖与砖之间不留空隙,
这样的地砖是( )
A.正五边形 B.正三角形,正五边形
C.正三角形,正五边形,正六边形 D.正三角形,正方形,正六边形
【答案】D
【解析】
解:若是正三角形地砖,正三角形的每个内角是 60°,能整除 360°,能够铺满地面;
若是正四角形地砖,正方形的每个内角是 90°,能整除 360°,能够铺满地面;
若是正五角形地砖,正五边形每个内角是 180°-360°÷5=108°,不能整除 360°,不能够铺满地面;
若是正六角形地砖,正六边形的每个内角是 120°,能整除 360°,能够铺满地面;
故选:D.