- 2021-05-26 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习北师大版专题四 统计与概率学案
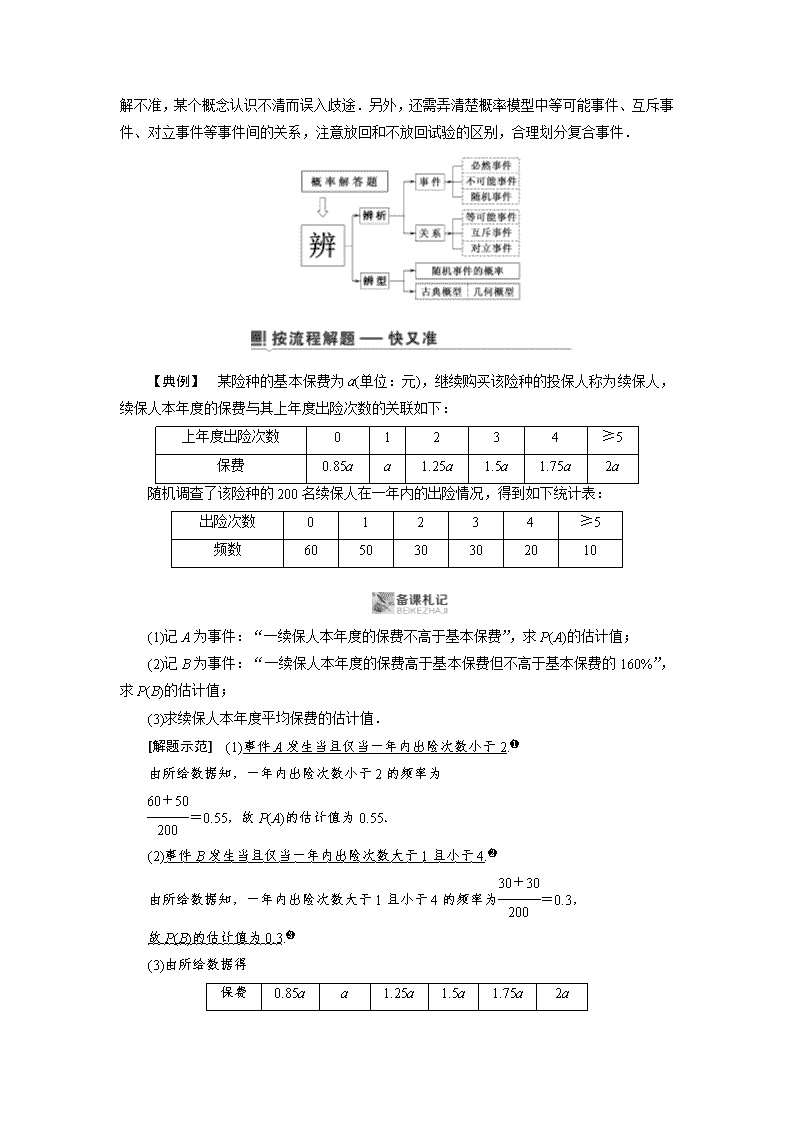
专题四 统计与概率 年份 卷别 小题考查 大题考查 2018 全国卷Ⅰ T3·饼图的识别与应用 T19·频数分布表、频率直方图及其应用(估计概率及计算平均数) 全国卷Ⅱ T5·古典概型的概率计算 T18·利用线性回归模型进行预测及线性回归模型的选择 全国卷Ⅲ T5·互斥事件的概率计算 T18·茎叶图、中位数、2×2列联表、K2的值 T14·随机抽样的判断 2017 全国卷Ⅰ T2·用样本的数字特征估计总体的数字特征 T19·相关系数的计算,均值、标准差公式的应用 T4·数学文化,有关面积的几何概型 全国卷Ⅱ T11·古典概型的概率计算 T19·频率分布直方图,频率估计概率,独立性检验 全国卷Ⅲ T3·折线图的识别与应用 T18·频数分布表,用频率估计概率 2016 全国卷Ⅰ T3·古典概型求概率 T19·柱状图、频数、平均值,用样本估计总体 全国卷Ⅱ T8·与时间有关的几何概型求概率 T18·频数、频率估计概率,平均值的应用 全国卷Ⅲ T4·统计图表的应用 T18·变量间的线性相关关系,回归方程的求解与应用 概率问题重在“辨”——辨析、辨型 概率问题的求解关键是辨别它的概率模型,只要找到模型,问题便迎刃而解.而概率模型的提取往往需要经过观察、分析、归纳、判断等复杂的辨析思维过程,常常因题设条件理解不准,某个概念认识不清而误入歧途.另外,还需弄清楚概率模型中等可能事件、 互斥事件、对立事件等事件间的关系,注意放回和不放回试验的区别,合理划分复合事件. 【典例】 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下: 上年度出险次数 0 1 2 3 4 ≥5 保费 0.85a a 1.25a 1.5a 1.75a 2a 随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表: 出险次数 0 1 2 3 4 ≥5 频数 60 50 30 30 20 10 (1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值; (2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值; (3)求续保人本年度平均保费的估计值. [解题示范] (1)事件A发生当且仅当一年内出险次数小于2.❶ 由所给数据知,一年内出险次数小于2的频率为 =0.55,故P(A)的估计值为0.55. (2)事件B发生当且仅当一年内出险次数大于1且小于4.❷ 由所给数据知,一年内出险次数大于1且小于4的频率为=0.3, 故P(B)的估计值为0.3.❸ (3)由所给数据得 保费 0.85a a 1.25a 1.5a 1.75a 2a 频率 0.30 0.25 0.15 0.15 0.10 0.05 调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+ 1.75a×0.10+2a×0.05=1.192 5a. 因此,续保人本年度平均保费的估计值为1.192 5a. ❶辨析:判断事件A包括试验发生的情况为:一年内出险次数小于2,即出险次数为0和1两种情况 ❷辨析:判断事件B所包含的基本事件 ❸辨型:随机事件的概率,并代入公式求解. 该部分往往与实际问题相结合,要注意理解实际问题的意义,使之和相应的概率计算对应起来,只有这样才能有效地解决问题.查看更多