- 2021-05-26 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
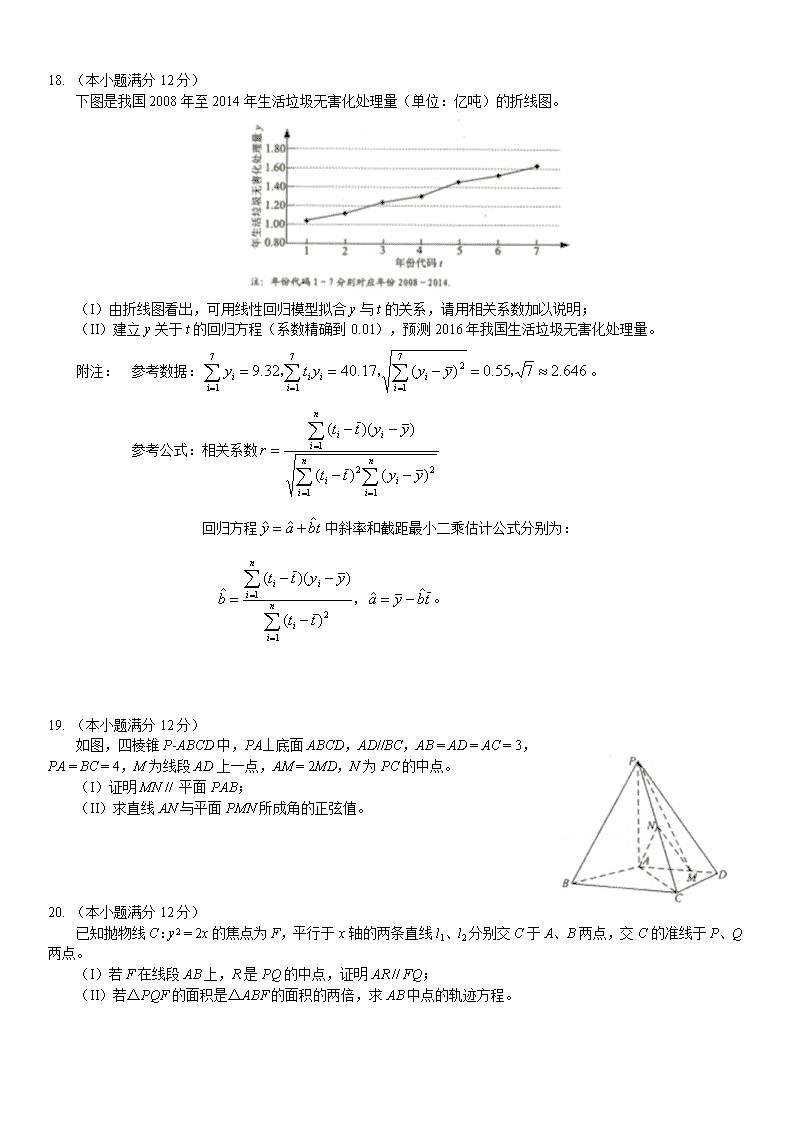
高考全国三卷理科数学试卷
2016.6 2016年普通高等学校招生全国统一考试(III卷) 理科数学 一、 选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符 合题目要求的。 1. 设集合,则S ∩ T = A. [2,3] B. C. D. 2. A. 1 B. -1 C. i D. -i 3. 已知向量,则∠ABC = A. 30° B. 45° C. 60° D. 120° 4. 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温 和平均最低气温的雷达图。图中A点表示十月的平均最高气温约15℃,B点 表示四月的平均最低气温约为5℃。下面叙述不正确的是 A. 各月的平均最低气温都在0℃以上 B. 七月的平均温差比一月的平均温差大 C. 三月和十一月的平均最高气温基本相同 D. 平均最高气温高于20℃的月份有5个 5. A. B. C. 1 D. 6. 已知,则 A. b < a < c B. a < b < c C. b < c < a D. c < a < b 7. 执行右面的程序框图,如果输入的a = 4,b = 6,那么输出的n = A. 3 B. 4 C. 5 D. 6 8. 在△ABC中,,BC边上的高等于BC,则sinA = A. B. C. D. 1. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该 多面体的表面积为 A. B. C. 90 D. 81 2. 在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB = 6, BC = 8,AA1 = 3,则V的最大值是 A. B. C. D. 3. 已知O为坐标原点,F是椭圆C:的左焦点,A、B分别为C 的左、右顶点。P为C上 一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E。若直线BM经过OE的中点,则C 的离心率为 A. B. C. D. 4. 定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k ≤ 2m,a1、a2…ak中的 0的个数不少于1的个数。若m = 4,则不同的“规范01数列”共有 A. 18个 B. 16个 C. 14个 D. 12个 二、 填空题:本题共4小题,每小题5分,共20分。 5. 设x、y满足约束条件则z = x + y的最大值为___________。 6. 函数的图象可由函数的图象至少向右平移_______个单位长度得到。 7. 已知f (x)为偶函数,当,则曲线y = f (x)在点(1,-3)处的切线方程是______________。 8. 已知直线l:交于A、B两点,过A、B分别作l的垂线与x轴交于C、 D两点,若|AB| = ,则|CD| =_______。 三、 解答题:共70分。解答应写出文字说明、证明过程或演算步骤。 17. (本小题满分12分) 已知数列{an}的前n项和。 (I) 证明{an}是等比数列,并求其通项公式; (II) 若。 18. (本小题满分12分) 下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图。 (I) 由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明; (II) 建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量。 附注: 参考数据:。 参考公式:相关系数 回归方程中斜率和截距最小二乘估计公式分别为: 。 19. (本小题满分12分) 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD//BC,AB = AD = AC = 3, PA = BC = 4,M为线段AD上一点,AM = 2MD,N为PC的中点。 (I) 证明MN // 平面PAB; (II) 求直线AN与平面PMN所成角的正弦值。 20. (本小题满分12分) 已知抛物线C:y2 = 2x的焦点为F,平行于x轴的两条直线l1、l2分别交C于A、B两点,交C的准线于P、Q两点。 (I) 若F在线段AB上,R是PQ的中点,证明AR // FQ; (II) 若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程。 19. (本小题满分12分) 设函数。 (I) 求; (II) 求A; (III) 证明。 请考生在第22、23、24题中任选一题作答。如果多做,则按所做的第一题计分。 20. (本小题满分10分)选修4—1:几何证明选讲 如图,⊙O中AB的中点为P,弦PC、PD分别交AB于E、F两点。 (I) 若∠PFB = 2∠PCD,求∠PCD的大小; (II) 若EC的垂直平分线与FD的垂直平分线交于点G,证明OG⊥CD。 21. (本小题满分10分)选修4—4:坐标系与参数方程 在直角坐标系xOy中,曲线C1的参数方程为。以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为。 (I) 写出C1的普通方程和C2的直角坐标系方程; (II) 设点P在C1上,点Q在C2上,求| PQ |的最小值及此时P的直角坐标。 22. (本小题满分10分)选修4—5:不等式选讲 已知函数。 (I) 当a = 2时,求不等式f (x) ≤ 6的解集; (II) 设函数。当,求a的取值范围。查看更多