- 2021-05-26 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省对口高考数学试卷
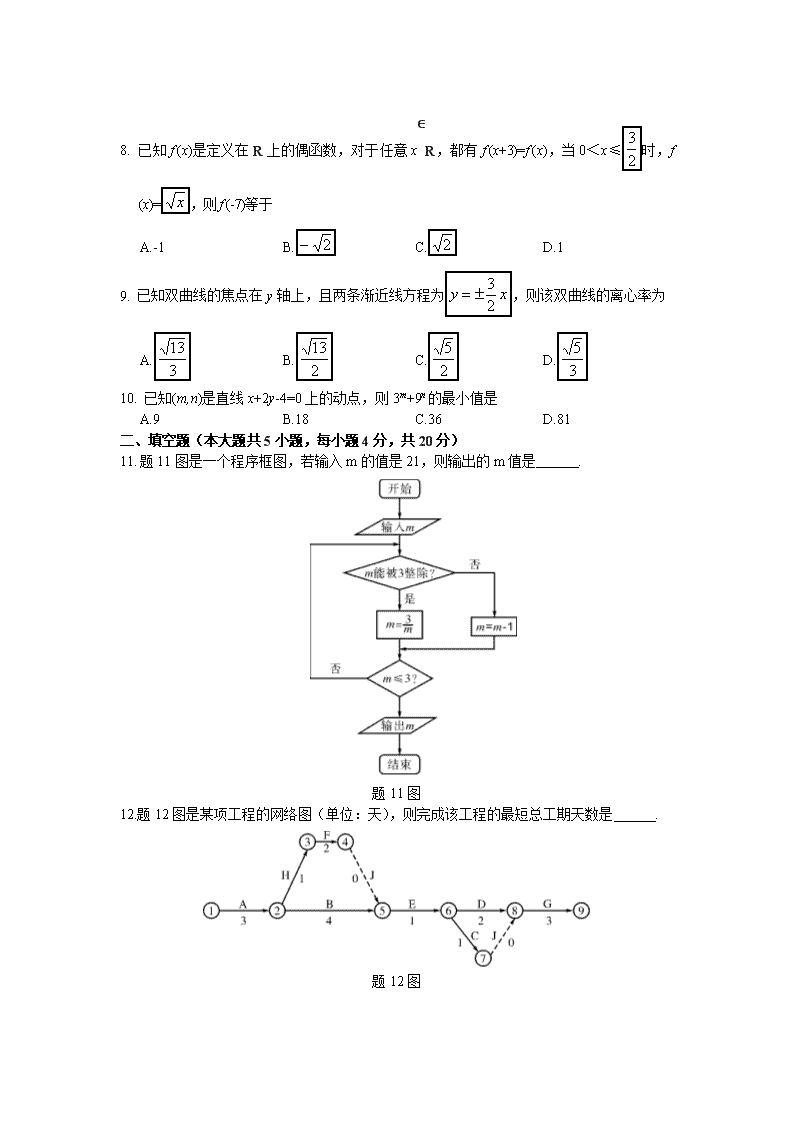
江苏省2019年普通高校对口单招文化统考 数 学 试卷 注 意 事 项 考生在答题前请认真阅读本注意事项及各题答题要求 1. 本试卷共4页,包含选择题(第1题~第10题,共10题)、非选择题(第11题~第23题,共13题)。本卷满分为150分,考试时间为120分钟。考试结束后,请将本试卷和答题卡一并交回。 2. 答题前,请务必将自己的姓名、考试证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。 3. 请认真核对监考员在答题卡上所粘贴的条形码上的姓名、考试证号与您本人是否相符。 4. 作答选择题(第1题~第10题),必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选择其它答案。作答非选择题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。 5. 如需作图,须用2B铅笔绘、写清楚。 一、单项选择题(本大题共10小题,每小题4分,共40分.在下列每小题中,选出一个正确答案,将答题卡上对应选项的方框涂满、涂黑) 1. 已知集合M ={1,3,5},N ={2,3,4,5},则M ∩ N等于 A.{3} B.{5} C.{3,5} D.{1,2,3,4,5} 2. 若复数z满足z·i=1+2i,则z的虚部为 A.2 B.1 C.-2 D.-1 3. 已知数组a=(2,-1,0),b=(1,-1,6),则a·b等于 A.-2 B.1 C.3 D.6 4. 二进制数(10010011)2换算成十进制数的结果是 A.(138)10 B.(147)10 C.(150)10 D.(162)10 5. 已知圆锥的底面直径与高都是2,则该圆锥的侧面积为 A. B. C. D. 6. 展开式中的常数项等于 A. B. C. D. 7. 若,则等于 A. B. C. D. 8. 已知f (x)是定义在R上的偶函数,对于任意x∈R,都有f (x+3)=f (x),当0<x≤时,f (x)=,则f (-7)等于 A.-1 B. C. D.1 9. 已知双曲线的焦点在y轴上,且两条渐近线方程为,则该双曲线的离心率为 A. B. C. D. 10. 已知(m,n)是直线x+2y-4=0上的动点,则3m+9n的最小值是 A.9 B.18 C.36 D.81 二、填空题(本大题共5小题,每小题4分,共20分) 11. 题11图是一个程序框图,若输入m的值是21,则输出的m值是 . 题11图 12.题12图是某项工程的网络图(单位:天),则完成该工程的最短总工期天数是 . 题12图 13.已知9a=3,则的周期是 . 14.已知点M是抛物线C:y2=2px(p>0)上一点,F为C的焦点,线段MF的中点坐标是(2,2),则p= . x>0 x≤0 15.已知函数f (x)= , 令g (x)=f (x)+x+a.若关于x的方程g (x)=2有两个实根,则实数a的取指范围是 . 三、解答题(本大题共8小题,共90分) 16.(8分)若关于x的不等式x2-4ax+4a>0在R上恒成立. (1)求实数a的取值范围; (2)解关于x的不等式. 17.(10分)已知f (x)是定义在R上的奇函数,当x≥0时,f (x)=log2(x+2)+(a-1)x+b,且 f (2)=-1.令an=f (n-3)(n∈N*). (1)求a,b的值; (2)求a1+a5+a9的值. 18.(12分)已知曲线C:x2+y2+mx+ny+1=0,其中m是从集合M={-2,0}中任取的一个数,n是从集合N={-1,1,4}中任取的一个数. (1)求“曲线C表示圆”的概率; (2)若m=-2,n=4,在此曲线C上随机取一点Q(x,y),求“点Q位于第三象限”的概率. 19.(12分)设△ABC的内角A,B,C的对边分别为a,b,c,已知2sin Bcos C-sin C=2sin A. (1)求角B的大小; (2)若b=2,a+c=4,求△ABC的面积. 20.(10分)通过市场调查知,某商品在过去的90天内的销售量和价格均为时间t(单位:天,t∈N*)的函数,其中日销售量近似地满足q(t)=36-t(1≤t≤90),价格满足 1≤t≤40 41≤t≤90 P(t)= ,求该商品的日销售额f (x)的最大值与最小值. 21.(14分)已知数列{an}的前n项和数列{bn}是各项均为正数的等比数列,且a1=b1,a6=b5. (1)求数列{an}的通项公式; (2)求数列{}的前n项和Tn; (3)求的值. 22.(10分)某房产开发商年初计划开展住宅和商铺出租业务.每套住宅的平均面积为80平方米,每套商铺的平均面积为60平方米,出租住宅每平方米的年利润是30元,出租商铺每平方米的年利润是50元,政策规定:出租商铺的面积不能超过出租住宅的面积,且出租的总面积不能超过48000平方米.若当年住宅和商铺的最大需求量分别为450套和600套,且开发的住宅和商铺全部租空,问房产开发商出租住宅和商铺各多少套,可使年利润最大?并求最大年利润. 23.(14分)已知圆O:x2+y2=r2(r>0)与椭圆C:相交于点M(0,1),N(0,-1),且椭圆的一条准线方程为x=-2. (1)求r的值和椭圆C的方程; (2)过点M的直线l另交圆O和椭圆C分别于A,B两点. ①若,求直线l的方程; ②设直线NA的斜率为k1,直线NB的斜率为k2,求证:k1=2k2 . 题23图查看更多