【数学】2019届理科一轮复习北师大版专题探究课6概率与统计中的高考热点问题教案

【数学】2019届理科一轮复习北师大版专题探究课6概率与统计中的高考热点问题教案

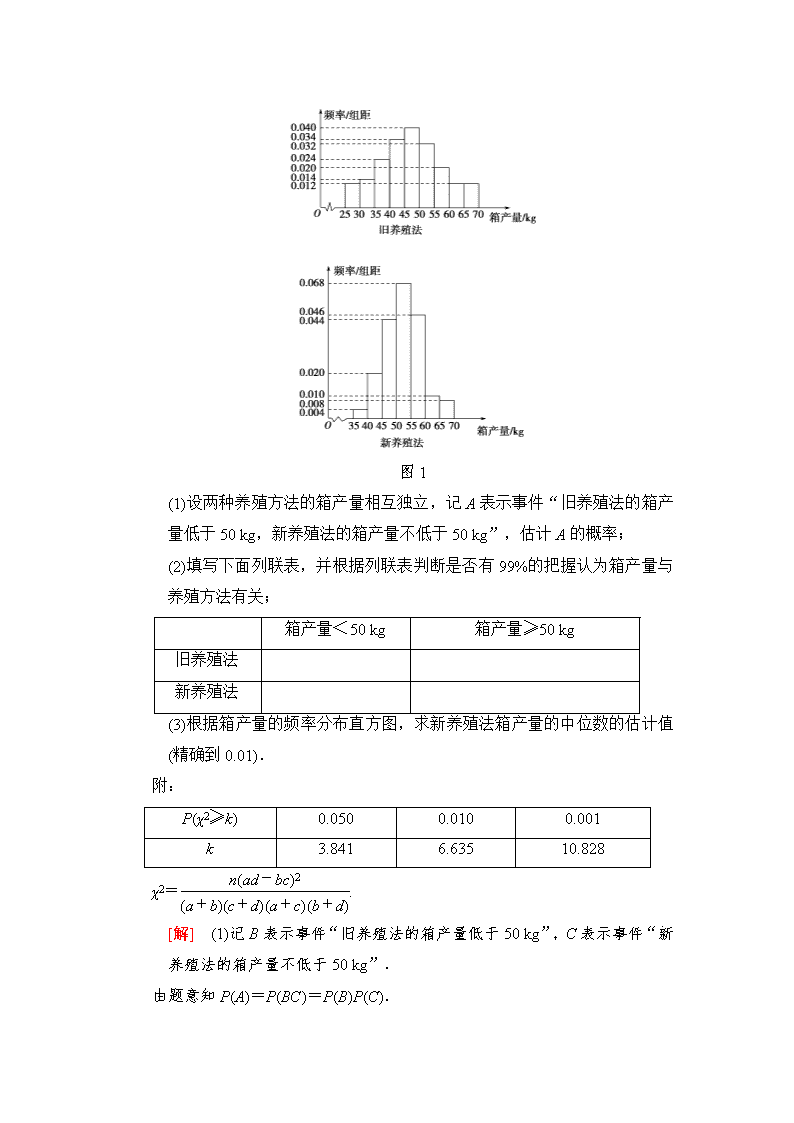
(六)　概率与统计中的高考热点问题 ‎(对应学生用书第193页)‎ ‎[命题解读]　1.概率与统计是高考中相对独立的一个内容，处理问题的方式、方法体现了较高的思维含量．该类问题以应用题为载体，注重考查应用意识及阅读理解能力、分类讨论与化归转化能力.2.概率问题的核心是概率计算，其中事件的互斥、对立、独立是概率计算的核心，排列组合是进行概率计算的工具，统计问题的核心是样本数据的获得及分析方法，重点是频率分布直方图、茎叶图和样本的数字特征，但近两年全国卷突出回归分析与独立性检验的考查.3.离散型随机变量的分布列及其均值的考查是历年高考的重点，难度多为中档类题目，特别是与统计内容渗透，背景新颖，充分体现了概率与统计的工具性和交汇性．‎ 统计与统计案例 以实际生活中的事例为背景，通过对相关数据的统计分析、抽象概括，作出估计、判断，常与抽样方法、茎叶图、频率分布直方图、概率等知识交汇考查，考查数据处理能力，分析问题，解决问题的能力．‎ ‎　(2017·全国卷Ⅱ)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量(单位：kg)，其频率分布直方图如图1所示：‎ 图1‎ ‎(1)设两种养殖方法的箱产量相互独立，记A表示事件“旧养殖法的箱产量低于50 kg，新养殖法的箱产量不低于50 kg”，估计A的概率；‎ ‎(2)填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关；‎ 箱产量＜50 kg 箱产量≥50 kg 旧养殖法 新养殖法 ‎(3)根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值(精确到0.01)．‎ 附：‎ P(χ2≥k)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎10.828‎ χ2＝.‎ ‎[解]　(1)记B表示事件“旧养殖法的箱产量低于50 kg”，C表示事件“新养殖法的箱产量不低于50 kg”．‎ 由题意知P(A)＝P(BC)＝P(B)P(C)．‎ 旧养殖法的箱产量低于50 kg的频率为 ‎(0.012＋0.014＋0.024＋0.034＋0.040)×5＝0.62，‎ 故P(B)的估计值为0.62.‎ 新养殖法的箱产量不低于50 kg的频率为 ‎(0.068＋0.046＋0.010＋0.008)×5＝0.66，‎ 故P(C)的估计值为0.66.‎ 因此，事件A的概率估计值为0.62×0.66＝0.409 2.‎ ‎(2)根据箱产量的频率分布直方图得列联表 箱产量＜50 kg 箱产量≥50 kg 旧养殖法 ‎62‎ ‎38‎ 新养殖法 ‎34‎ ‎66‎ χ2＝≈15.705.‎ 由于15.705>6.635，故有99%的把握认为箱产量与养殖方法有关．‎ ‎(3)因为新养殖法的箱产量频率分布直方图中，箱产量低于50 kg的直方图面积为(0.004＋0.020＋0.044)×5＝0.34<0.5，‎ 箱产量低于55 kg的直方图面积为 ‎(0.004＋0.020＋0.044＋0.068)×5＝0.68>0.5，‎ 故新养殖法箱产量的中位数的估计值为 ‎50＋≈52.35(kg)．‎ ‎[规律方法]　1. 独立性检验就是考察两个分类变量是否有关系，利用独立性检验，能够帮助我们对日常生活中的实际问题作出合理的推断和预测，并能较为准确地给出这种判断的可信度；具体做法是根据公式χ2＝，计算随机变量的观测值χ2，χ2值越大，说明“两个变量有关系”的可能性越大.‎ ‎2.频率分布直方图中的众数、中位数与平均数.‎ (1)最高的小长方形底边中点的横坐标即是众数；‎ (2)平分频率分布直方图的面积且垂直于横轴的直线与横轴交点的横坐标是中位数；‎ (3)平均数是频率分布直方图的“重心”‎ ‎，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.‎ ‎[跟踪训练]　(2018·成都二诊)某项科研活动共进行了5次试验，其数据如下表所示：‎ 特征量 第1次 第2次 第3次 第4次 第5次 x ‎555‎ ‎559‎ ‎551‎ ‎563‎ ‎552‎ y ‎601‎ ‎605‎ ‎597‎ ‎599‎ ‎598‎ ‎(1)从5次特征量y的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；‎ ‎(2)求特征量y关于x的线性回归方程y＝bx＋a，并预测当特征量x为570时，特征量y的值．‎ ‎(附：回归直线的斜率和截距的最小二乘法估计公式分别为b＝，a＝－b)‎ ‎[解]　(1)记“至少有一个大于600”为事件A．‎ ‎∴P(A)＝1－＝.‎ ‎(2)＝＝556，‎ ＝＝600.‎ ‎∴b＝＝＝0.3.‎ ‎∵a＝－b＝600－0.3×556＝433.2，‎ ‎∴线性回归方程为y＝0.3x＋433.2.‎ 当x＝570时，y＝0.3×570＋433.2＝604.2.‎ ‎∴当x＝570时，特征量y的估计值为604.2.‎ 常见概率模型的概率 几何概型、古典概型、相互独立事件与互斥事件的概率是高考的热点，几何概型主要以客观题进行考查，求解的关键在于找准测度(面积、体积或长度)；相互独立事件，互斥事件常作为解答题的一问考查，也是进一步求分布列、均值与方差的基础，求解该类问题要正确理解题意，准确判定概率模型，恰当选择概率公式．‎ ‎　在某校教师趣味投篮比赛中，比赛规则是：每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖．已知教师甲投进每个球的概率都是.‎ ‎(1)记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及均值；‎ ‎(2)求教师甲在一场比赛中获奖的概率．‎ ‎[解]　(1)X的所有可能取值为0,1,2,3,4,5,6.‎ 依条件可知，X～B，P(X＝k)＝C·· (k＝0,1,2,3,4,5,6)．‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ P 故EX＝(0×1＋1×12＋2×60＋3×160＋4×240＋5×192＋6×64)＝＝4.或因为X～B6，，所以EX＝6×＝4.‎ ‎(2)设教师甲在一场比赛中获奖为事件A，‎ 则P(A)＝C··＋C··＋＝，即教师甲在一场比赛中获奖的概率为.‎ ‎[规律方法]　首先判断随机变量X服从二项分布是问题解决的突破口，对于实际问题中的随机变量X，如果能够断定它服从二项分布B(n，p) ‎，则其概率、均值与方差可直接利用公式P(X＝k)＝Cpk(1－p)n－k(k＝0，1，2，…，n)，EX＝np，DX＝np(1－p)求得，因此，利用二项分布的相关公式，可以避免烦琐的运算过程，提高运算速度和准确度.‎ ‎[跟踪训练]　甲、乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错或不答都得0分，已知甲队3人每人答对的概率分别为，，，乙队每人答对的概率都是，设每人回答正确与否相互之间没有影响，用ξ表示甲队总得分．‎ ‎(1)求ξ＝2的概率；‎ ‎(2)求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．‎ ‎[解]　(1)ξ＝2，则甲队有两人答对， 一人答错，‎ 故P(ξ＝2)＝××＋××＋××＝；‎ ‎(2)设甲队和乙队得分之和为4为事件A，甲队比乙队得分高为事件B．设乙队得分为η，则η～B.‎ P(ξ＝1)＝××＋××＋××＝，‎ P(ξ＝3)＝××＝，‎ P(η＝1)＝C··＝，‎ P(η＝2)＝C··＝，‎ P(η＝3)＝C＝，‎ ‎∴P(A)＝P(ξ＝1)P(η＝3)＋P(ξ＝2)P(η＝2)＋P(ξ＝3)·P(η＝1)＝×＋×＋×＝，‎ P(AB)＝P(ξ＝3)·P(η＝1)＝×＝，‎ ‎∴所求概率为P(B|A)＝＝＝.‎ 离散型随机变量的分布列、期望和方差的应用 离散型随机变量及其分布列、均值与方差及应用是高考的一大热点，每年均有解答题，属于中档题．复习中应强化应用题的理解与掌握，弄清随机变量的所有取值是正确列随机变量分布列和求均值与方差的关键，对概率的确定与转化是解题的基础，准确计算是解题的核心．‎ ‎　(本小题满分12分)(2016·全国卷Ⅰ)某公司计划购买2台机器，该种机器使用三年后即被淘汰．‎ 机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.①‎ 现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面如图2所示的柱状图：②‎ 图2‎ 以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X表示2台机器三年内共需更换的易损零件数，③‎ n表示购买2台机器的同时购买的易损零件数．‎ ‎(1)求X的分布列；‎ ‎(2)若要求P(X≤n)≥0.5，④确定n的最小值；‎ ‎(3)以购买易损零件所需费用的期望值为决策依据，在n＝19与n ‎＝20之中选其一，应选用哪个？‎ ‎[审题指导]‎ 题眼 挖掘关键信息 ‎①‎ 看到这种条件，想到解题时可能要分类求解 ‎②‎ 看到柱状图想到频数与频率间的关系，想到横轴中的取值含义 ‎③‎ 看到自变量X想到柱状图，想到X的所有可能取值 ‎④‎ 看到P(X≤n)≥0.5想到X和n的含义，想到(1)中的分布列 ‎[规范解答]　(1)由柱状图及以频率代替概率可得，一台机器在三年内需更换的易损零件数为8,9,10,11的概率分别为0.2,0.4,0.2,‎0.2. 1‎分 由题意可知X的所有可能取值为16，17，18，19，20，21，22.⑤‎ 从而P(X＝16)＝0.2×0.2＝0.04；‎ P(X＝17)＝2×0.2×0.4＝0.16；‎ P(X＝18)＝2×0.2×0.2＋0.4×0.4＝0.24；‎ P(X＝19)＝2×0.2×0.2＋2×0.4×0.2＝0.24；‎ P(X＝20)＝2×0.2×0.4＋0.2×0.2＝0.2；‎ P(X＝21)＝2×0.2×0.2＝0.08；‎ P(X＝22)＝0.2×0.2＝‎0.04. 4‎分 所以X的分布列为 X ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ P ‎0.04‎ ‎0.16‎ ‎0.24‎ ‎0.24‎ ‎0.2‎ ‎0.08‎ ‎0.04‎ ‎ 6分 ‎(2)由(1)知P(X≤18)＝0.44，P(X≤19)＝0.68，⑥‎ 故n的最小值为19. 7分 ‎(3)记Y表示2台机器在购买易损零件上所需的费用(单位：元)．‎ 当n＝19时，⑦‎ EY＝19×200×0.68＋(19×200＋500)×0.2＋(19×200＋2×500)×0.08＋(19×200＋3×500)×0.04＝4 040； 9分 当n＝20时，⑧‎ EY＝20×200×0.88＋(20×200＋500)×0.08＋(20×200＋2×500)×0.04＝4 080. 11分 可知当n＝19时所需费用的期望值小于当n＝20时所需费用的期望值，故应选n＝19. 12分 ‎[阅卷者说]‎ 易错点 防范措施 ‎⑤忽视X的实际含义导致取值错误，进而导致概率计算错误 细心审题，把握题干中的重要字眼，关键处加标记，同时理解X取每个值的含义 ‎⑥忽视P(X≤n)≥0.5的含义，导致不会求解 结合(1)中的分布列及n的含义，推理求解便可 ‎⑦、⑧忽视n＝19与n＝20的含义导致无法解题 本题中购买零件所需费用包含两部分，一部分为购买机器时购买零件的费用，另一部分为备件不足时额外购买的费用 ‎[规律方法]　解答离散型随机变量的分布列及相关问题的一般思路：‎ (1)明确随机变量可能取哪些值.‎ (2)结合事件特点选取恰当的计算方法计算这些可能取值的概率值.‎ (3)根据分布列和期望、方差公式求解.‎ 易错警示：明确离散型随机变量的取值及事件间的相互关系是求解此类问题的关键.‎ ‎[跟踪训练]　某网站用“10分制”调查一社区人们的治安满意度．现从调查人群中随机抽取16名，如图3茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎，小数点后的一位数字为叶)．‎ 图3‎ ‎(1)若治安满意度不低于9.5分，则称该人的治安满意度为“极安全”．求从这16人中随机选取3人，至多有1人是“极安全”的概率；‎ ‎(2)以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)中任选3人，记X表示抽到“极安全”的人数，求X的分布列、均值与方差. ‎ ‎【导学号：79140382】‎ ‎[解]　(1)设Ai表示所取3人中有i个人是“极安全”，且i＝0,1,2,3.至多有1人是“极安全”记为事件A，则A＝A0＋A1，‎ 所以P(A)＝P(A0)＋P(A1)＝＋＝.‎ ‎(2)由茎叶图可知，16人中任取1人是“极安全”的概率 P＝＝，依题意，X～B，‎ 则P(X＝k)＝C ，k＝0,1,2,3.‎ 所以P(X＝0)＝＝，‎ P(X＝1)＝C××＝，‎ P(X＝2)＝C××＝，P(X＝3)＝＝.‎ X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P EX＝0×＋1×＋2×＋3×＝.‎ 或EX＝np＝.‎ DX＝np(1－p)＝3××＝.‎ ‎ ‎ 概率与统计的综合应用 概率与统计作为考查考生应用意识的重要载体，已成为近几年高考的一大亮点和热点．主要依托点是统计图表，正确认识和使用这些图表是解决问题的关键，复习时要在这些图表上下功夫，把这些统计图表的含义弄清楚，在此基础上掌握好样本特征数的计数方法、各类概率的计算方法及均值与方差的运算．‎ ‎　(2017·全国卷Ⅰ)为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸(单位：cm)．根据长期生产经验，可以认为这条生产线在正常状态下生产的零件的尺寸服从正态分布N(μ，σ2)．‎ ‎(1)假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在(μ－3σ，μ＋3σ)之外的零件数，求P(X≥1)及X的数学期望；‎ ‎(2)一天内抽检零件中，如果出现了尺寸在(μ－3σ，μ＋3σ)之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．‎ ‎①试说明上述监控生产过程方法的合理性；‎ ‎②下面是检验员在一天内抽取的16个零件的尺寸：‎ ‎9.95　10.12　9.96　9.96　10.01　9.92　9.98　10.04 ‎ ‎10.26　9.91　10.13　10.02　9.22　10.04　10.05　9.95‎ 经计算得＝xi＝9.97，s＝＝≈0.212，其中xi为抽取的第i个零件的尺寸，i＝1,2，…，16.‎ 用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对当天的生产过程进行检查．剔除(－3，＋3)之外的数据，用剩下的数据估计μ和σ(精确到0.01)．‎ 附：若随机变量Z服从正态分布N(μ，σ2)，则P(μ－3σ

查看更多