高考数学压轴题突破140之立体几何五种动态问题和解题绝招

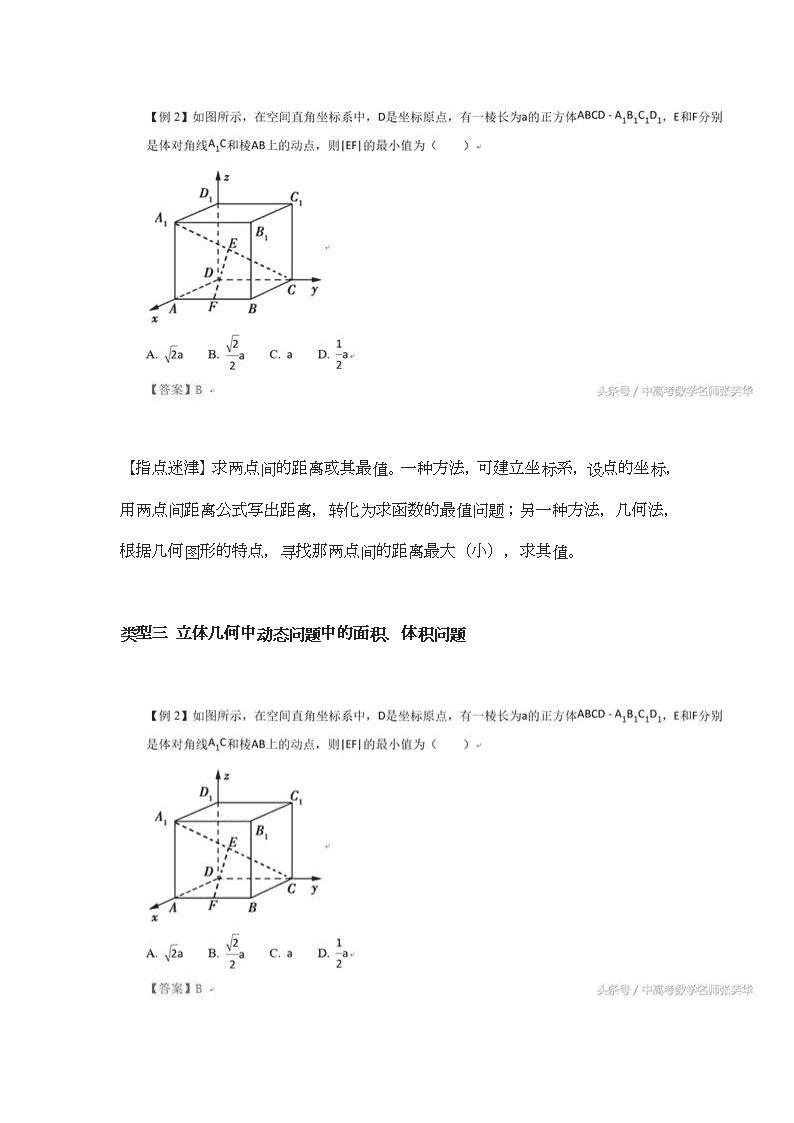
高考数学压轴题突破140之立体几何五种动态问题和解题绝招

‎2018年高考数学压轴题突破140之立体几何五种动态问题和解题绝招 中高考数学名师张芙华 2018-01-29 06:14:27‎ ‎2018年高考数学压轴题突破140之立体几何五种动态问题和解题绝招 一．方法综述 立体几何的动态问题是高考的热点，问题中的“不确定性”与“动感性”元素往往成为学生思考与求解问题的思维障碍，使考题的破解更具策略性、挑战性与创新性。一般立体动态问题形成的原因有动点变化、平面图形的翻折、几何体的平移和旋转以及投影与截面问题，由此引发的常见题型为动点轨迹、角度与距离的计算、面积与体积的计算、探索性问题以及有关几何量的最值求解等。此类题的求解并没有一定的模式与固定的套路可以沿用，很多学生一筹莫展，无法形成清晰的分析思路，导致该题成为学生的易失分点。究其原因，是因为学生缺乏相关学科素养和解决问题的策略造成的。‎ 动态立体几何题在变化过程中总蕴含着某些不变的因素，因此要认真分析其变化特点，寻找不变的静态因素，从静态因素中，找到解决问题的突破口。求解动态范围的选择、填空题，有时应把这类动态的变化过程充分地展现出来，通过动态思维，观察它的变化规律，找到两个极端位置，即用特殊法求解范围。对于探究存在问题或动态范围（最值）问题，用定性分析比较难或繁时，可以引进参数，把动态问题划归为静态问题。具体地，可通过构建方程、函数或不等式等进行定量计算，以算促证。‎ 二．解题策略 类型一立体几何中动态问题中的角度问题 ‎【指点迷津】空间的角的问题，一种方法，代数法，只要便于建立空间直角坐标系均可建立空间直角坐标系，然后利用公式求解；另一种方法，几何法，几何问题要结合图形分析何时取得最大（小）值。当点M在P处时，EM与AF所成角为直角，此时余弦值为0（最小），当M点向左移动时，EM与AF所成角逐渐变小时，点M到达点Q时，角最小，余弦值最大。‎ 类型二 立体几何中动态问题中的距离问题 ‎【指点迷津】求两点间的距离或其最值。一种方法，可建立坐标系，设点的坐标，用两点间距离公式写出距离，转化为求函数的最值问题；另一种方法，几何法，根据几何图形的特点，寻找那两点间的距离最大（小），求其值。‎ 类型三 立体几何中动态问题中的面积、体积问题 ‎【指点迷津】求几何体体积的最值，先观察几何图形三棱锥，其底面的面积为不变的几何量，求点P到平面BCD的距离的最大值，选择公式，可求最值。‎ 类型四 立体几何中动态问题中的轨迹问题 类型五 立体几何中动态问题中的翻折、旋转问题